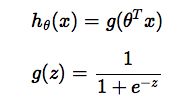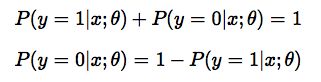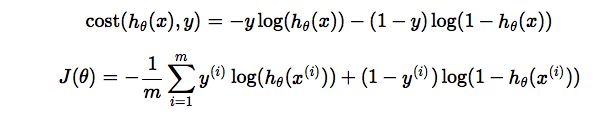[方法转]http://www.powerxing.com/logistic-regression-in-python/
http://blog.csdn.net/lipengcn/article/details/49592221
机器学习公开课:http://www.cnblogs.com/python27/p/MachineLearningWeek03.html
逻辑回归梯度下降法详解:http://blog.csdn.net/lookqlp/article/details/51161640
http://blog.sae.sina.com.cn/archives/3888
不调用包:http://blog.csdn.net/zouxy09/article/details/20319673
http://blog.csdn.net/lsldd/article/details/41551797
参数调优:http://www.weixinla.com/document/31127980.html
【总结】
逻辑回归找到最优化的参数有2种方法,这两种方法得出的最优结果是一致的,有时候容易弄混淆。这里总结一下:
方法1:利用最大似然函数方法(样本出现概率最大)
参考上述【http://blog.csdn.net/lookqlp/article/details/51161640】
求出每个样本出现的概率,再把所有样本出现的概率表达式计算出来,利用最大似然函数求出整体出现概率最大时的参数θ。
预测函数:
按照求最大似然函数的方法,逻辑回归似然函数:
我们的目标是求最大l(θ)时的θ,如上函数是一个上凸函数,可以使用梯度上升来求得最大似然函数值(最大值)。或者上式乘以-1,变成下凸函数,就可以使用梯度下降来求得最小负似然函数值(最小值):
可以在似然函数前加一个1/m,构成与线性回归类似形式的损失函数:
J(θ)=−(1/m)*l(θ)
利用梯度下降法求出θ即可。
方法2:利用损失函数最小法
参考:【 http://www.cnblogs.com/python27/p/MachineLearningWeek03.html】
构造预测函数:
解释:
此外由于y只能取0或者1两个值,换句话说,一个数据要么属于0分类要么属于1分类,假设已经知道了属于1分类的概率是p,
那么当然其属于0分类的概率则为1-p,这样我们有以下结论:
构造损失函数:(注意与线性模型的损失函数不同)
简化上述函数形式,即得最终损失函数:
m是样本数,是平均误差损失loss的,预防两次样本不一样导致的损失函数值差异很大。
**【注意】方法2的损失函数与方法1的似然函数完全一致。而且也是用梯度下降方法找出时损失函数最小的θ,故结果与方法1是一致的。
***梯度下降的方法的推导:
自己 写的实例:
源数据excel表,内容如下:
| age | amount | grade | gender |
| 18 | 208182 | 6 | 0 |
| 18 | 26141 | 8 | 1 |
| 18 | 325354 | 9 | 0 |
| 18 | 183147 | 5 | 1 |
| 18 | 13923 | 5 | 1 |
import os
import codecs
import numpy as np
import pandas as pd
import statsmodels.api as sm
import pylab as pl
import csv
#数据读入,变量准备
os.chdir('/Users/zhangb/Desktop/python学习文件')
df=pd.read_excel('model.xlsx','工作表1')
dummy_ranks=pd.get_dummies(df['gender'],prefix='gender') #定义哑变量
cols_to_keep=['age','amount','grade']
data=df[cols_to_keep].join(dummy_ranks.ix[:,'gender_1':]) #分2类,保留一个哑变量类别
#print(data.head())
data['intercept']=1 #加入截距项
# 执行逻辑回归 把gender当做要预测的分类变量
trains=data.columns[0:3]
logit=sm.Logit(data['gender_1'],data[trains])
result=logit.fit()
#print(result.summary())
#预测
import copy
combos=copy.deepcopy(data)
pred=combos.columns[0:3]
combos['intercept']=1
combos['predict']=result.predict(combos[pred])
a=result.predict(combos[pred])
total=0
hit=0
for value in combos.values: #统计预测效果
predict=value[-1]
gender=int(value[3])
if predict >0.5:
total +=1
if gender==1:
hit +=1
#输出结果
print('total:%d,hit:%d,precision:% .2f' %(total,hit,100*hit/total))
print(combos.head())
print(pred)
print(a[1:10])
#结果导入csv;txt文件
vv=combos.values #去除pandas数据的所有值
pp=list(vv)
#结果数据导入csv文件
with open ('output.csv','w',newline='') as data2:
bb=csv.writer(data2,dialect=('excel'))
bb.writerow(['age','amount','grade','gender_1','intercept','predict'])
bb.writerows(pp)
data2.close
#结果数据导入txt文件
f1=open('out.txt','w')
for i in pp:
a1=list(i)
a2=str(a1)[1:-1].replace(',','')
f1.write(a2+'\n')
f1.close()
=============完========
#小练习语句
#df = pd.read_csv('model.csv','r',encoding='gbk')
#print(df.head())
#print (df['gender'][0:4])
#print(df.columns)
#print (df.describe())
#print (df.std())
#print(df[0:3])
#print(df.head())
#print(df.iloc[0:3,1:3])
#print(pd.crosstab(df['gender'],df['grade'],rownames=['gender'])) 交叉表
#df.hist()
#pl.show()