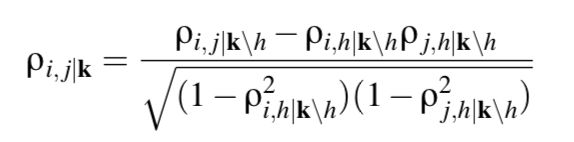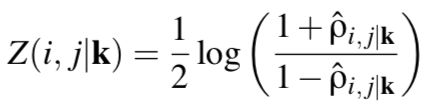因果分析,PC算法(PC Algorithm)
转载:https://github.com/Renovamen/pcalg-py
PC Algorithm
理想情况(知道所有条件独立关系)
Estimating High-Dimensional Directed Acyclic Graphs with the PC-Algorithm, Markus Kalisch, Peter Bu ̈hlmann. 2007

line 11: 需要条件独立关系
偏相关系数
校正其它变量后某一变量与另一变量的相关关系,校正的意思可以理解为假定其它变量都取值为均数
服从高斯分布的随机变量,条件独立性与偏相关系数为0等价:
假设随机变量 X X X 服从多元高斯分布,对于 i ≠ j ∈ ( 1 , . . . , p ) , k ⊆ ( 1 , . . . , p ) / ( i , j ) i \not =j∈(1, ..., p),k⊆(1, ..., p) /\ (i,j) i=j∈(1,...,p),k⊆(1,...,p)/ (i,j),用 ρ i , j ∣ k ρ_{i,j|k} ρi,j∣k 表示 X ( i ) X(i) X(i) 和 X ( j ) X(j) X(j) 与 X ( r ) ( r ∈ k ) X^{(r)} (r∈k) X(r)(r∈k) 之间的偏相关系数 。 当且仅当 X ( i ) X(i) X(i) 和 X ( j ) X( j ) X(j) 条件独立与 X ( r ) ( r ∈ k ) X^{(r)} (r∈k) X(r)(r∈k) 时, ρ i , j ∣ k = 0 ρ_{i,j|k}=0 ρi,j∣k=0。
∴ 条件独立性可由偏相关估计出来,条件独立性检验转偏相关系数检验
任意两个变量 i , j i, j i,j的 h h h(排除其他 h h h个变量的影响后, h < = k − 2 h<=k-2 h<=k−2)阶样本偏相关系数:
Fisher Z Test( ρ ≠ 0 ρ\not=0 ρ=0时的显著性检验)
ρ ≠ 0 ρ\not=0 ρ=0时不是正态分布,不能进行 t t t 检验。将 ρ ρ ρ 进行 Fisher Z 转换,转换后可以认为是正态分布。
Fisher’s z-transform:
零假设: H 0 ( i , j ∣ k ) : ρ i , j ∣ k ≠ 0 H_0(i,j|k): ρ_{i,j|k} \not= 0 H0(i,j∣k):ρi,j∣k=0
对立假设: H 1 ( i , j ∣ k ) : ρ i , j ∣ k = 0 H_1(i,j|k): ρ_{i,j|k} = 0 H1(i,j∣k):ρi,j∣k=0
当 n − ∣ k ∣ − 3 ∣ Z ( i , j ∣ k ) > Φ − 1 ( 1 − α / 2 ) \sqrt{n-|k|-3}|Z(i,j|k)>Φ^{-1}(1-α/2) n−∣k∣−3∣Z(i,j∣k)>Φ−1(1−α/2), H 0 H_0 H0成立
∴ 用 n − ∣ k ∣ − 3 ∣ Z ( i , j ∣ k ) < = Φ − 1 ( 1 − α / 2 ) \sqrt{n-|k|-3}|Z(i,j|k)<=Φ^{-1}(1-α/2) n−∣k∣−3∣Z(i,j∣k)<=Φ−1(1−α/2)替换 PC-Algorithm 中的“如果 i , j i,j i,j 被 k k k d − s e p a r a t i o n d-separation d−separation”
paper: Frequency Distribution of the Values of the Correlation Coefficient in Samples from an Indefinitely large population, Fisher, R.A., 1915
R语言实现
zStat(x, y, S, C): 计算并返回 n − ∣ k ∣ − 3 ∣ Z ( i , j ∣ k ) \sqrt{n-|k|-3}|Z(i,j|k) n−∣k∣−3∣Z(i,j∣k)的值
pcorOrder(i, j, k, C): 计算并返回 i i i 和 j j j 与 k k k 的偏相关系数
condIndFisherZ(x, y, S, C): 计算 n − ∣ k ∣ − 3 ∣ Z ( i , j ∣ k ) \sqrt{n-|k|-3}|Z(i,j|k) n−∣k∣−3∣Z(i,j∣k),返回它是否<= cutoff
gaussCItest(x, y, S, suffStat): 计算并返回 Φ − 1 ( 1 − α / 2 ) Φ^{-1}(1-α/2) Φ−1(1−α/2)
CPDAG
An algorithm for fast recovery of sparse causal graphs, Peter Spirtes, Clark N. Glymour., 1990
得到骨架(无向图)。
任意 BN 的马尔科夫等价类都存在唯一的 CPDAG 与之等价,因此, CPDAG可作为贝叶斯网络等价类的图形化表示
将骨架扩展为等价类的CPDAG:
Causal inference and causal explanation with background knowledge, Meek., 1995
一些定义:
骨架:把有向图 G G G 的有向边变成无向边。
PDAG:设 G = ( V , E ) G = (V, E) G=(V,E) 是一个图,若边集 E E E 中包含有向边和无向边,则称 是一个部分有向图。若部分有向图 中不存在有向圈,则称 是一个部分有向无环图(PDAG)
马尔科夫等价:贝叶斯网络 < G 1 , P 1 >
有向无环图 G = ( V , E ) G = (V, E) G=(V,E) ,任意有向边 V i → V j ∈ E V_i \rightarrow V_j ∈ E Vi→Vj∈E,若存在图 G ′ = ( V , E ′ ) G' = (V, E') G′=(V,E′) 与 G G G 等价,且 V j → V i ∈ E ′ V_j \rightarrow V_i ∈ E' Vj→Vi∈E′,则称有向边 V i → V j V_i \rightarrow V_j Vi→Vj 在 G G G 中是可逆的,否则是不可逆的.。
同理, 对任意无向边 V i → V j ∈ E V_i \rightarrow V_j ∈ E Vi→Vj∈E,若存在 G 1 = ( V , E 1 ) G_1 = (V, E_1) G1=(V,E1)、 G 2 = ( V , E 2 ) G_2 = (V, E_2) G2=(V,E2) 均与 G G G 等价,且 V i → V j ∈ E 1 V_i \rightarrow V_j ∈ E_1 Vi→Vj∈E1、 V j → V i ∈ E 2 V_j \rightarrow V_i ∈ E_2 Vj→Vi∈E2, 则 称 无 向边 V i → V j V_i \rightarrow V_j Vi→Vj 在 G G G 中是可逆的,否则是不可逆的
CPDAG:设 G = ( V , E ) G = (V, E) G=(V,E) 是一个部分有向无环图,若 E E E 中的有向边都是不可逆的,并且 E E E 中的无向边都是可逆的,则称 G G G 是一个完全部分有向无环图(CPDAG)