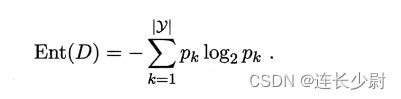周志华《机器学习》习题4.4——python实现基于信息熵进行划分选择的决策树算法

1.题目

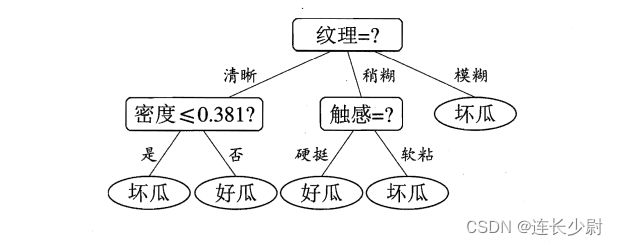
试编程实现基于信息熵进行话饭选择的决策树算法，并为表4.3中数据生成一棵决策树。
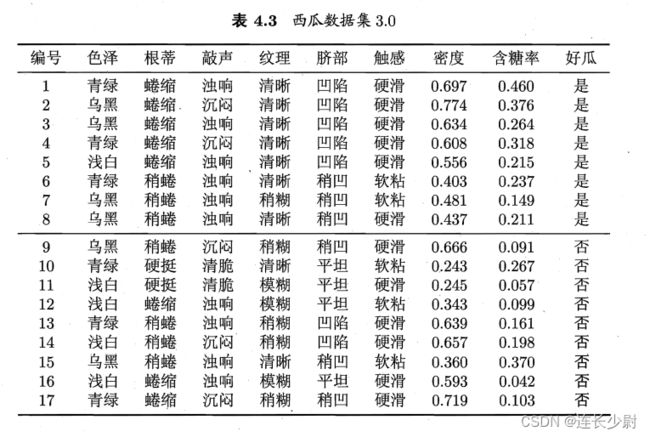
表4.3如下：
另外再附个txt版的，下次可以复制粘贴：

青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.460,是
乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.360,0.370,否
浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

2.代码

先定义节点类，这里设计的每个节点包含三个属性：
a： 表示当前用于划分数据集的属性
result： 若当前节点为叶节点，result存储类别
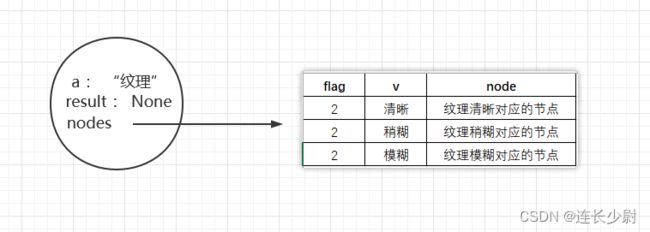
nodes： 为当前节点的子节点列表，列表元素格式为(flag, v, node)，flag可以为0、1、2三种值，0和1表示当前用于划分选择的属性是连续值，其中flag为0表示当前元素的node的a属性都 小于 v，同理，flag为1表示当前元素的node的a属性都大于v，当flag为2，则表示划分选择的属性是离散值，表示当前元素node的a属性等于v。

画图说明比较直观，比如，如果根节点按照“纹理”这个属性划分西瓜，则跟节点的存储结构的是:

import numpy as np
import matplotlib.pyplot as plt

class Node:
    def __init__(self, a, result, nodes:list):
        self.a = a
        self.result = result
        self.nodes = nodes
    def __init__(self):
        self.a = None
        self.result = None
        self.nodes = []
    def is_leaf(self):
        if len(self.nodes) == 0 or self.nodes == None:
            return True
        else:
            return False
    def __str__(self):
        return "划分属性：" + str(self.a) + ' ' + "划分值：" + ','.join([str(vi[1]) for vi in self.nodes]) + ' ' + "结果：" + str(self.result)

读数据函数，这里直接将汉字直接作为x中的值了：

def read_data(dir):
    xigua = []
    with open(dir, "r+") as f:
        for line in f.readlines():
            xigua.append(line.split(','))
        x = []
        y = []
        for i in range(len(xigua)):
            x.append(xigua[i][:8])
            x[i][6] = float(x[i][6])
            x[i][7] = float(x[i][7])
            if '是' in xigua[i][8]:
                y.append(1)
            else:
                y.append(0)
        
    return x, y

然后是决策树生成代码，一个节点有三种情况会导致划分结束，从而变成叶子节点：
1.数据集全部为一类，不用划分
2.数据集属性全部相同（但不是一类），无法划分，并且划分结果类别是父节点中类别较多的类
3.数据集为空，同样，划分结果类别是父节点中类别较多的类

def tree_generate(x:np.array, y:np.array, A:set):
    node = Node()
    if is_one_category(y):
        node.result = y[0]
        return node
    elif len(A) == 0 or is_all_same(x):
        node.result = find_most_category(y)
        return node
    
    #   寻找最佳划分属性，同时返回划分结果
    best_a, div_result = find_best_a(x, y, A)
    
    A1 = A.copy()
    A1.remove(best_a)
    node.a = best_a
    
    for di in div_result:
        flag = di[0]
        v = di[1]
        dv_x = di[2]
        dv_y = di[3]
        new_node = tree_generate(dv_x, dv_y, A1)
        if len(dv_x) == 0:
            new_node.is_leaf = True
            new_node.result = find_most_category(y)
        else:
            node.nodes.append((flag, v, new_node))
        
    return node    

然后是寻找最佳划分属性代码，通过找最大的信息增益，然后取对应的属性作为划分属性。另外，因为在计算信息增益的过程中会把数据划分好，所以这里直接就把计算过程划分好的数据保留到best_div_result中了，外层函数就无需再次划分数据了。

def find_best_a(x, y, A):
    max_gain = 0
    best_div_result = []
    
    for ai in A:
        t_gain, div_result = gain(x, y, ai) 
        if t_gain > max_gain:
            best_div_result = div_result
            max_gain = t_gain
            best_a = ai
    return best_a, best_div_result

然后是计算信息增益的代码，这里首先有个判断，用来分开处理属性是离散值和连续值的情况。
信息增益公式：

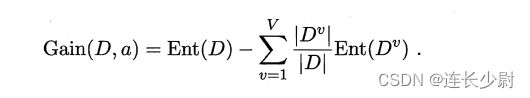
def gain(x, y, a):
    sum_x = len(x)
    possible_value = set()
    possible_value_f = []
    final_div_result = []
    
    if type(x[0][a]) == float:
        sort(x, y, a)
        for i in range(len(x)-1):
            possible_value_f.append((x[i][a] + x[i+1][a])/2)
            
        max_gain = 0
        for v in possible_value_f:
            y_small = []
            x_small = []
            y_big = []
            x_big = []
            for i in range(len(x)):
                if x[i][a] < v:
                    x_small.append(x[i])
                    y_small.append(y[i])
                else:
                    x_big.append(x[i])
                    y_big.append(y[i])
            t_gain = ent(y) - len(y_small)/sum_x * ent(y_small) - len(y_big)/sum_x  * ent(y_big)
            if t_gain > max_gain:
                max_gain = t_gain
                # (flag, v, x, y) ： flag为0表示该部分数据被分到小于v的节点上，为1表示该部分数据被分到大于v的节点上，为2表示等于v
                final_div_result = [(0, v, x_small, y_small), (1, v, x_big, y_big)]
                
        return max_gain, final_div_result
    else:
        for xi in x:
            possible_value.add(xi[a])
        result = ent(y)
        for v in possible_value:
            dv_num = 0
            dv_x = []
            dv_y = []
            for i in range(len(x)):
                if x[i][a] == v:
                    dv_num += 1
                    dv_y.append(y[i])
                    dv_x.append(x[i])
            final_div_result.append((2, v, dv_x, dv_y))
            result -= dv_num/sum_x * ent(dv_y)
        return result, final_div_result

冒泡排序，因为对于属性是连续值的情况需要取（数据个数-1）个中位数，所以需要先排序每条数据。

def sort(x, y, a):
    for i in range(len(x)-1):
        for j in range(len(x)-i-1):
            if x[j][a] > x[j+1][a]:
                t = x[j]
                x[j] = x[j+1]
                x[j+1] = t
                t = y[j]
                y[j] = y[j+1]
                y[j+1] = t

计算节点信息熵的函数，公式：

def ent(y):
    y_set = set()
    for yi in y:
        y_set.add(yi)
        
    result = 0
    sum_y = len(y)
    
    for k in y_set:
        dk_num = 0
        for yi in y:
            if yi == k:
                dk_num += 1
        result -= (dk_num/sum_y)*np.math.log2(dk_num/sum_y)
    
    return result

其他函数：

# 寻找数据中比较多的类别
def find_most_category(y):
    num = {}
    for yi in y:
        if num.get(yi) == None:
            num[yi] = 1
        else:
            num[yi] = num[yi] + 1
    result_num = 0
    for k in num.keys():
        if num[k] > result_num:
            result_num = num[k]
            result = k
    return result

# 判断每条数据是否属性值全部相同
def is_all_same(x):
    for i in range(len(x)):
        if np.any(x[i] != x[0]):
            return False
    return True
  
# 数据集是否全部属于一个类别
def is_one_category(y):
    c = y[0]
    for i in range(len(y)):
        if y[i] != c:
            return False
    return True

# 对生成的决策树进行展示（先序遍历）
def show_tree(node:Node, d):
    print("第",d,"层：")
    print(node)
    for nodei in node.nodes:
        show_tree(nodei[2], d+1)

主函数：

if __name__ == "__main__":
    x, y = read_data("./xigua.txt")
    A = list(range(len(x[0])))
    root = tree_generate(x, y, A)
    show_tree(root, 1)

3.运行结果

这里没有写画出树的代码，就直接先序遍历顺序打印出来了，同时打印出了节点的层数（根节点是第一层），可以手动画出图。（划分属性是一个数，对应训练集中属性下标）
根据书中对比，可以看到结果是正确的。