2. 使用机器学习或者深度学习对羽毛进行等级识别判断
使用机器学习或者深度学习对羽毛进行等级识别判断
1. 运行环境
- CPU:I5-10400
- 内存:16GB
- 系统:Win10 64位专业版,20H2
- IDE:Pycharm2020.1
- Python:3.7.9
- Pytorch:1.7.1
2. 实验目的
- 理解机器学习如何应用到实际场景。
- 掌握特征提取方法。
3. 实验内容
- 数据集介绍:在制作羽毛球时,羽毛会根据质量的高低而价格不同,因此存在根据羽毛的图片而对其分级的需求。本数据集种羽毛共分为 5 个级别,分别是1、2、3、4、56 级,其中1级有1353 张图片,2级有 432 张图片,3 级有 163 张图像,4 级有 172 张图像,56 级有 42 张图像。训练集验证集按 7:3 的比例划分,划分结果在train.txt与val.txt中保存。
- 在给出的训练图片上训练一个羽毛的等级判断模型,在验证集上进行测试,其中评价指标分为 2 个,第一个是准确率,第二个是每一级别的召回率(如 2 级羽毛共 100 根,实际测试,2 级的 100 根中有 80 根识别成了 2 级,则 2 级的召回率为 80%)。
- 采用深度学习的方法来自动提取特征然后进行训练。
4. 实验思路
-
选择 2015 年微软实验室提出的 ResNet 网络(残差网络)。
本实验采用ResNet34模型,结构如图1所示。ResNet提出残差结构,并搭建超深的网络结构;使用Batch Normalization加速训练。在ResNet网络提出之前,传统的卷积神经网络都是通过将一系列卷积层与下采样层进行堆叠得到的。但是当堆叠到一定网络深度时,就会出现两个问题。1)梯度消失或梯度爆炸。 2)退化问题(degradation problem)。在ResNet论文中说通过数据的预处理以及在网络中使用BN(Batch Normalization)层能够解决梯度消失或者梯度爆炸问题。但是对于退化问题(随着网络层数的加深,效果还会变差)并没有很好的解决办法,所以ResNet论文提出了residual结构(残差结构)来减轻退化问题。
-
使用给定的数据集,利用
resnet34-pre.pth模型预训练的权重进行模型训练实验。 -
通过每轮迭代计算准确率,并根据训练好的模型计算每个级别的召回率。
5. 实验步骤
整体实验步骤如图2所示。
5.1 图像加载和处理
将图像随机裁剪为不同的大小和宽高比,缩放所裁剪得到的图像为制定的大小。然后以给定的概率随机水平旋转给定的 PIL 的图像,默认为 0.5。然后将图像转为 Tensor,并作归一化处理。
data_transform = {
"train": transforms.Compose([transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])]),
"val": transforms.Compose([transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])])}
data_root = os.path.abspath(os.path.join(os.getcwd())) # get data root path
image_path = os.path.join(data_root, "data_res") # flower data set path
assert os.path.exists(image_path), "{} path does not exist.".format(image_path)
train_dataset = datasets.ImageFolder(root=os.path.join(image_path, "train"),
transform=data_transform["train"])
5.2 定义卷积神经网络
这里使用的是 ResNet34 网络模型。
class ResNet(nn.Module):
def __init__(self, block, blocks_num, num_classes=1000, include_top=True):
super(ResNet, self).__init__()
self.include_top = include_top
self.in_channel = 64
self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2,
padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(self.in_channel)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, blocks_num[0])
self.layer2 = self._make_layer(block, 128, blocks_num[1], stride=2)
self.layer3 = self._make_layer(block, 256, blocks_num[2], stride=2)
self.layer4 = self._make_layer(block, 512, blocks_num[3], stride=2)
if self.include_top:
self.avgpool = nn.AdaptiveAvgPool2d((1, 1)) # output size = (1, 1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
def resnet34(num_classes=1000, include_top=True):
return ResNet(BasicBlock, [3, 4, 6, 3], num_classes=num_classes, include_top=include_top)
5.3 定义损失函数和优化器
定义损失函数,CrossEntropyLoss 为交叉熵损失函数。定义 Adam 优化器,根据模型当前参数决定优化即调整参数的增减和幅度。Ir 为学习率。过大过小都会影响准确率。
loss_function = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.0001)
5.4 调用Model的API进行训练
选择 ResNet34 网络并加载预先下载好的 resnet34-pre.pth 模型权重。
net = resnet34()
model_weight_path = "./resnet34-pre.pth"
5.5 迭代输出训练准确率
遍历迭代 10 次。首先遍历数据集,返回数据 data 和步长 step。把 data 数组中的图像和标签分别赋值给变量 images 和 label,清空之前的梯度信息。然后开始进行正向传播,并把图像计算与设备进行绑定。训练得到预测输出之后与真实标签进行计算损失值。将 loss 反向传播到各个节点,更新每个节点参数。
for epoch in range(10):
# train
net.train()
running_loss = 0.0
for step, data in enumerate(train_loader, start=0):
images, labels = data
optimizer.zero_grad()
logits = net(images.to(device))
loss = loss_function(logits, labels.to(device))
loss.backward()
optimizer.step()
running_loss += loss.item()
rate = (step+1)/len(train_loader)
a = "*" * int(rate * 50)
b = "." * int((1 - rate) * 50)
print("\rtrain loss: {:^3.0f}%[{}->{}]{:.4f}".format(int(rate*100), a, b, loss), end="")
print()
每轮迭代的准确率计算:
net.eval()
acc = 0.0
with torch.no_grad():
for val_data in validate_loader:
val_images, val_labels = val_data
outputs = net(val_images.to(device))
predict_y = torch.max(outputs, dim=1)[1]
acc += (predict_y == val_labels.to(device)).sum().item()
val_accurate = acc / val_num
if val_accurate > best_acc:
best_acc = val_accurate
torch.save(net.state_dict(), save_path)
print('[epoch %d] train_loss: %.3f test_accuracy: %.3f' %
(epoch + 1, running_loss / step, val_accurate))
5.6 计算召回率
在测试集中分别为 1,2,3,4,56 类的图片分类计算召回率。
classes = ('1', '2', '3', '4', '56')
N_CLASSES = 5
class_correct = list(0. for i in range(N_CLASSES))
class_total = list(0. for i in range(N_CLASSES))
model.eval()
total_correct = 0
total_num = 0
start = time.perf_counter()
for x, label in validate_loader:
x, label = x.to(device), label.to(device)
logits = model(x)
pred = logits.argmax(dim=1)
total_correct += torch.eq(pred, label).float().sum().item()
total_num += x.size(0)
c = (pred == label).squeeze()
for i in range(len(label)):
_label = label[i]
class_correct[_label] += c[i].item()
class_total[_label] += 1
acc = total_correct / total_num
print('acc: ', acc)
for i in range(N_CLASSES):
print('Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
end = time.perf_counter()
print("FPS: %f" % (val_num / (end - start)))
6. 实验结果
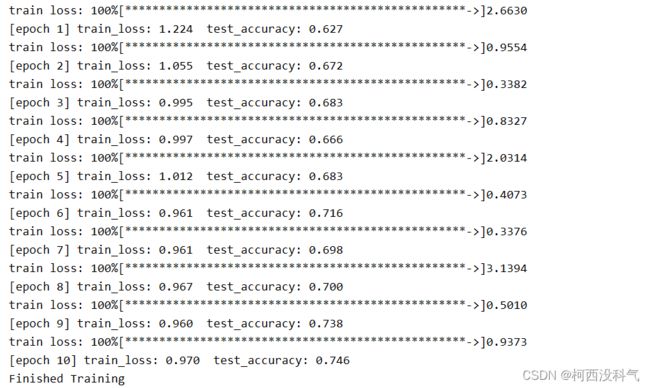
- 训练准确率
训练准确率如图3所示,经过 10 次迭代,训练集的最高准确率达到了 74.6%。
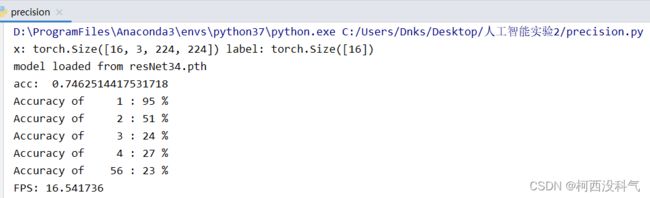
- 召回率
各级羽毛的召回率如图4所示。1类、2类、3类、4类、56 类各类的召回率分别是 95%、51%、24%、27% 和 23%。总体正确率达到了 74.6%。
7. 结果分析
由于训练样本数量不多,训练的准确率只到了 74.6%。在测试集中,1 类的数据量比较多,模型训练后的准确度能够达到 95%,而由于 2、3,4、56 类的测试样本数量过少,准确率并不高,训练效果一般。