机器学习（0）：机器学习概述及基本概念

最近自己会把自己个人博客中的文章陆陆续续的复制到CSDN上来，欢迎大家关注我的 个人博客，以及我的github。

一、序言

机器学习（machine learning）是当前计算机专业的一大热门，也是我研究生几年需要学习的内容之一。虽然之前粗略的学过一点皮毛，但是当初笔记做的实在不好，这次趁着看吴恩达老师的机器学习教学视频以及李航老师的《统计学习方法》，重新整理一下自己的笔记，同时也是整理一下自己的思路。

该系列估计会有10余篇的文章，可能主要包括机器学习的基本知识、线性回归、logistic回归、softmax回归、决策树、随机森林、聚类算法、支持向量机（SVM）、EM算法、隐马尔可夫模型（HMM）等内容。文章的顺序大概会从易到难，从常用到不常用的顺序来写，后期尽量每篇补充几个配套的代码。由于本人比较懒，所以什么时候更新新的文章，就看时间和心情了。

作为该系列的第一篇文章，本文将会介绍机器学习算法的概念，以及凸函数、梯度下降算法、损失函数、正则化有/无监督学习以及最大似然函数等内容。

二、一点建议

由我浅薄的机器学习经验来说，我认为机器学习比较适合刚考完研或者大学数学基础比较好的人来学，因为在学习过程中经常会遇到公式的推导，所以学习的人应该有较好的微积分知识（主要是求导）、概率论的基础知识和最大似然估计，以及线性代数中矩阵的逆、转置、乘法等基本运算。在邹博老师的机器学习课上，还介绍了矩阵的求导，这在推导公式也可能会遇到。此外最好有一定的编程基础，可以让算法落地。

三、课程资源

我所了解到的机器学习方面比较不错的图书有：周志华的《机器学习》，俗称西瓜书；李航的《统计学习方法》等。我当前正在看《统计学习方法》，里面的机器学习算法大都是从数学的角度进行讲解的，所以需要一定的数学功底，虽然有些地方看不懂，但是感觉讲得真是好，知识点也比较全。有关的教学视频我推荐两个：一个是吴恩达老师的机器学习；另一个是邹博老师的机器学习和深度学习课程。只能说两位老师各有千秋，我一开始看的是邹博老师的，因为他的视频有配套的代码资源，讲的也比较形象，涉及的内容比较广，也比较注重公式推导。而吴恩达老师的比较经典，但是没有配套的代码，有些机器学习算法没有讲到。所以就看大家自己的选择了。另外免费附上一个上述网站对应的邹博机器学习与深度学习2019课件，提取码是：8ykz。

四、机器学习概述

首先要明确一点，机器学习和机器人没有半毛钱关系，可以理解为计算机（程序）通过大量的数据不断学习如何解决特定的问题。机器学习是人工智能的一个领域，人们希望通过它来像人类一样较为智能处理各种问题，而我们经常听到的深度学习又是机器学习的一个分支。通过机器学习算法，我们可以解决数据预测、数据分类，甚至是音频、图像等的处理等问题。

有一种有关机器学习的定义是：程序通过利用经验E在解决一个任务T的过程中，性能P得到了一定的改善，则说该程序从经验E中进行了学习。这个定为稍显抽象，举个栗子，如果让程序完成对邮件进行是否是垃圾邮件的分类问题，那么通常我们需要给程序大量的已经标注好的是否是垃圾邮件的邮件，程序通过对其进行分析，并建立数学模型（可以理解为一个有很多参数的数学表达式或概率分布）。对于一个新的邮件，将其输入到该数学模型中，就会得到一个输出，该输出表示是否是垃圾邮件，或者是垃圾邮件的概率。而机器学习的过程就是在构建数学模型的时候程序自动的学习模型的参数的过程。

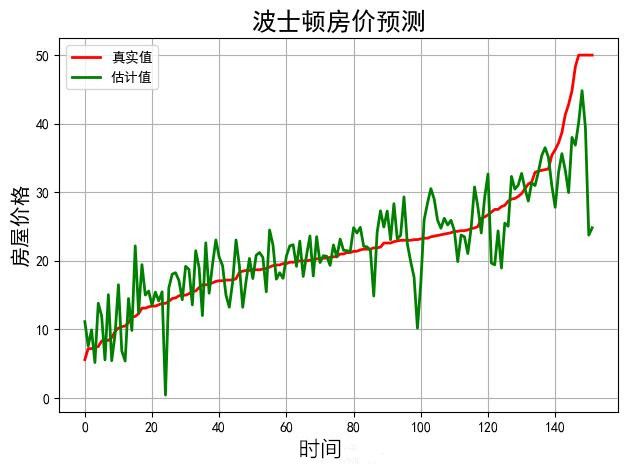
在学习机器学习时，我们经常会看到类似于下图这样的图片。下图是用机器学习算法预测房价，图中绿线是某个房子的房价随时间的波动情况，而红线是对房价的估计（或者说“拟合”），那么对于一个新的时间点，则只要看对应的红线的值就可以对房价进行预测了。

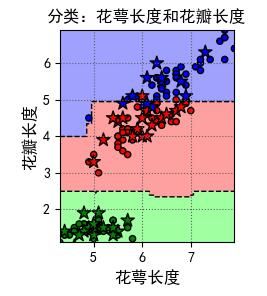
下图是利用机器学习算法，根据花萼长度和花瓣长度对花进行分类。其中蓝、红、绿三个区域表示预测得到的不同类别所包含的区域，而形状不一的点表示花的真实分类。

五、基本概念

下面讲解的概念有点多了，读者可能一时难以消化，当前只需要了解它们分别是做什么用的，以及它们的运行过程是什么样的即可。等后面的讲解提到的时候再来查看也不迟。

1.分类和回归

分类（classification）和回归（regression）模型的本质是一样的，其中输入变量和输出变量均为离散变量的预测问题是分类问题，反之，均为连续变量的为回归问题。例如上面提到的对房价的预测就是回归问题，而对花的分类就是分类问题。

2.训练集、测试集和验证集

上面提到过，机器学习算法就是用现有的样本构建一个模型，然后用该模型去对新的数据进行预测。那么问题来了，我们用什么来判断预测结果的好坏呢？如果用同样的数据去构建和测试模型显然不合理。这个时候通常把样本划分为训练集（training set）和测试集（test set），其中训练集就是用来训练（构建）模型的那部分样本，而测试集就是测试已经构建的模型好坏的那部分样本。而验证集（validation set）则是在交叉验证时用来挑选最优模型的那部分样本。以上三个集合之间均无交集。

3.交叉验证

当已有的样本数据不够多时，为了得到更好的模型就可以采取交叉验证（cross validation）的方式。它的主要思想就是重复的使用样本数据。在简单交叉验证中可以将样本随机划分为训练集和测试集两部分，然后在各种条件（比如不同参数数目）下用训练集训练模型，再用测试集对模型的误差进行评估，从而选出误差最小的模型。除了简单交叉验证之外，还有S折交叉验证和留一交叉验证等，原理都是差不多的，这里就不再赘述了。

4.有/无监督学习

有监督学习就是指在对给定的样本构建模型时，给定的样本中包含数据真实的值，也就是说给定的是有标签数据，而无监督学习则正好与之相反。例如在对花分类的例子中，如果只给出每朵花的花萼长度和花瓣长度，而不给出花所属的真实类别，这就属于无监督学习。而如果也给出了花的所属的真实类别，则就是有监督学习。

5.假设函数和损失函数

假设函数（hypothesis function）可以理解为我们所构建的模型，可以用$h_{\theta }(x)$来表示，对于一个输入$ x_i$，则输出为 $h_{\theta }(x_i)$。其实也可以简写为h(x)。

损失函数（loss function）又称代价函数（cost function）或误差函数，是一种对模型的好坏进行评估的方法，它的做法通常是通过计算真实值与预测值之间的误差来实现。常用的损失函数有很多，例如：

(1)均方误差（mean-square error, MSE）函数

其公式为：
$$MSE=\frac{1}{n}\sum _{i=1}^n(y-\hat{y}{)}^2$$
其中n是样本个数，y和$\hat{y}$分别是样本的真实值和假设函数所给出的预测值。

0-1损失函数

其公式为：

也就是当真实值和预测值相等时损失为0，反之为1。

除此之外，还有交叉熵损失等，这里不再一一赘述。

6.过拟合和正则化

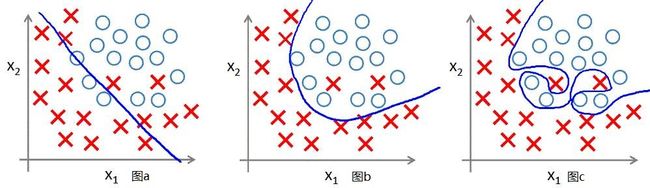
为了防止所建立的模型过拟合（overfitting），可以为损失函数增加正则化项。所谓过拟合就是模型对训练集数据预测效果非常好，而对测试集数据则预测效果不好。也可以说泛化能力（对新样本的适应能力）差。如下图中的图c就是过拟合了。

表现在房价预测的例子上就是房价的估值（红线）会经过每一个样本点，但是如果要对新的房价进行预测则效果很差。为什么红线经过每个样本点效果反而变差了呢，这主要是因为模型的复杂度太高了，所以因为增加一个正则化项来对模型的复杂度进行限制，也就是对参数进行惩罚。常用的正则化方式有L1正则和L2正则等。

L1正则：

$$L1(\theta )=\sum _{i=1}^m|{\theta }_i|$$

L2正则：

$$L2(\theta )=\sum _{i=1}^m{\theta }_i^2$$

其中$\theta$是模型的参数向量，m是参数的个数。L1正则又称LASSO。

要注意区分损失函数和正则化，正则化是为了防止模型过拟合而对模型复杂度做的惩罚，而损失函数是评判预测结果好坏的标准，损失函数往往由真实值和预测值之间的误差加上正则化项而组成。

7.凸函数和梯度下降

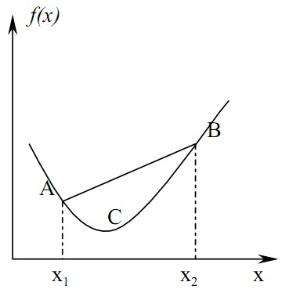
机器学习中提到的凸函数（convex function）和平常我们在数学中接触到的凸函数有些不同，机器学习中的凸函数是数学中的下凸函数，这种函数的优势是它只有一个全局最小值点，这为什么是优势还请先来看一下梯度下降算法（gradient descent）的含义。

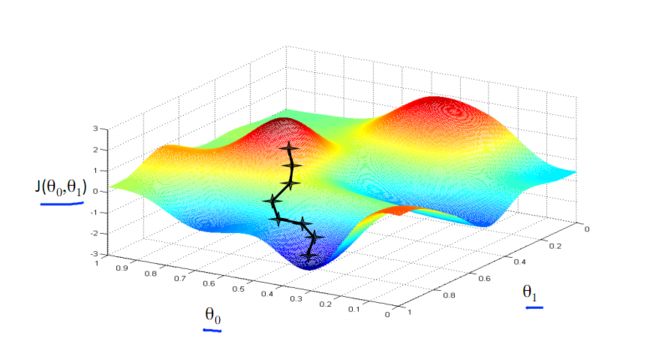
想象一下你现在在一座山的靠近山顶的位置，如果你想尽快下山，那么一个可行的方法是每次朝高度变化最大的方向（即负梯度方向）走一小步，那么就可以到达一个局部最低点。而从靠近山峰的另一个地方按照该方法下山又可以到达另一个局部最低点。为了获取全局最低点，那么应该要求目标函数（一般指损失函数）是一个凸函数，这样就保证了只有一个全局极（最）小值点。熟悉算法的同学可以理解为这是一个贪心算法，而凸函数则保证了局部最优解就是全局最优解。

梯度下降算法的提出主要是为了可以让计算机迭代的求解模型中参数的最优值，这可以让模型的参数 theta 每次都朝最优的方向更新，通过有限次更新到达最优值。该过程可表示为：

Repeat until convergence{
$${\theta }_j:={\theta }_j-\alpha \nabla h_{\theta }(x)$$
}

下三角表示求导，上式表示第j个参数更新为其原来值减去$\alpha$倍的导数方向。$\alpha$又被称为学习率（learning rate），这个概念等以后用到的时候再讲，现在只需要了解它是用来调整每次更新的幅度的。大家可能有个疑问：参数$\theta$的初始值该怎么确定呢？答案是对其进行随机初始化。

在机器学习中，梯度下降算法以及其他优化算法关心的是损失函数在何时取极小值，而并不关心极小值是多少。

如果先计算出所有样本在某点的平均梯度方向再对参数进行更新，则称之为批量梯度下降（batch gradient decline），而如果只用一个样本计算梯度方向并对参数进行更新，则称之为随机梯度下降（stochastic gradient descent，SGD），但是SGD存在模型收敛慢的问题，所以可以取以上两者的折中——mini-batch梯度下降，也就是每次用若干个样本梯度的平均方向作为更新的方向。

8.最小二乘法和正规方程

最小二乘法中二乘就是平方的意思，它是指：把使得测量值和真实值之间误差的平方和最小的测量值y当作真实值。可以用公式表示为：
$$\underset{y}{\min }(\sum (y-\hat{y}{)}^2)\Rightarrow 真值y$$
关于最小二乘法的详细介绍，请参考文章：如何理解最小二乘法？

在求解最优的参数值时，除了可以用梯度下降算法，还可以用正规方程（normal equation）的方法来进行求解，正规方程和最小二乘法息息相关，如果把最小二乘法的公式写为矩阵的形式，然后对参数$\theta$求导就可以得到以下正规方程的公式，也就是当平方和误差最小时参数的取值：
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$
其中，X是m*n的矩阵，即由m个样本，n个特征组成的矩阵，y是m*1的向量，即m个样本的真实值组成的向量。

该方法的优势时不必设置学习率，也不用迭代求解。但是需要求逆矩阵，所以当n比较大（大于1w）时，求解速度很慢。并且不知道大家有没有注意到一个问题，当式子中的逆矩阵不存在时，就不能用上述公式计算了，这时可以用矩阵的伪逆来代替矩阵的逆进行求解。关于伪逆的知识可以自行百度。

9.特征缩放

不知道你有没有想过一个问题，当给你一对样本数据，你该怎么对它进行建模呢？首先得确定用哪些特征，比如在房价预测中，可以根据房子的面积、房子的使用年数、离市中心的距离等可以量化的特征来对其价格进行预测。当然选取的特征不是越多越好，必要时还需对其进行筛选。当选取多个特征时，如果特征之间的取值范围相差较大时，就可能会导致梯度下降的速度变慢，所以应该保证特征的取值范围在同一尺度内，取值范围太大或太小都是不好的。这时候就需要对特征进行缩放，可以使用以下公式来实现：
$$feature=\frac{feature-mean}{max-min}$$
公式中几个标记分别代表特征值、平均值、最大值和最小值

10.极大似然估计

极大似然估计又称最大似然估计，“似然”就是“可能性”的意思。它可以解决“模型已定，参数未知”的情况，即当给定一堆样本数据，想要预测它们的模型已经选定，但是最优的参数还没有确定的情况下，就可以用极大似然估计来求解使得模型产生出观测数据的概率最大的最优参数。

设总体样本的概率分布为：p(x;$\theta$)，其中$\theta$是未知参数，则求最大似然估计量的$\theta$一般步骤为：

​ （1）写出似然函数：

​
$$L(\theta )=\prod _{i=1}^{n}p(x_i;\theta )$$
​ （2）对似然函数取对数得$\ln L(\theta )$，并整理;

​ （3）对参数$\theta$求导数，并令其为0:
$$\frac{\partial \ln L(\theta )}{\partial {\theta }_j}=0$$
​ （4）解以上似然方程，得到最优的参数$\theta$。