使用线性回归来进行每个人的平均医疗费用预测

先贴出代码如下:

insurance<-read.csv("insurance.csv",stringsAsFactors = FALSE)
ins_model<-lm(expenses~.,data = insurance)
summary(ins_model)

(

ins_model<-lm(expenses~.,data = insurance)

这句话的意思就是以insurance为数据源,建立expenses和数据源其他属性的(一次)线性关系. "."表示其他所有属性

)

R语言分析数据的一个很大的优势就是它有很多的第三方包，可以很方便我们使用。所以上面的代码很简介。但是，我们关键是要知道怎么来分析数据。

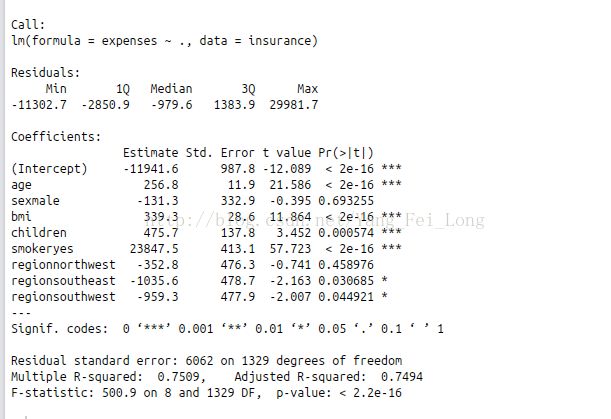
首先我们先看看结果吧:

1.Residuals表示残差，顾名思义，就是指预测的数据和实际的数据的差值。从四分图可以看出，最大和最小的误差值都挺大的，这说明了线性回归算法在预测极端值的时候，效果并不是很理想。但是可以看出1Q,Median,3Q (也就是在1/4值，1/2值,3/4值)的差距不是很大，所以可以判断出整个值的分布类似正态分布，集中误差在-979左右。

2.还有一个关键的点是:Multiple R-squared,叫做多元R方值。例子中，这个值等于0.7509.表明该线性预测的结果适合75%的案例，也可以说成功为75%.

但是，但是。。。。。75%，这在应用中根本就无法接受,所以，我们需要优化。优化的第一步，就是要分析数据:

在我们获得数据之后，就要开始观察数据。 大多数都是通过str(insurance)来分析有多少条数据，以及每条数据有多少个属性，然后是每个属性值又是怎么分布的。

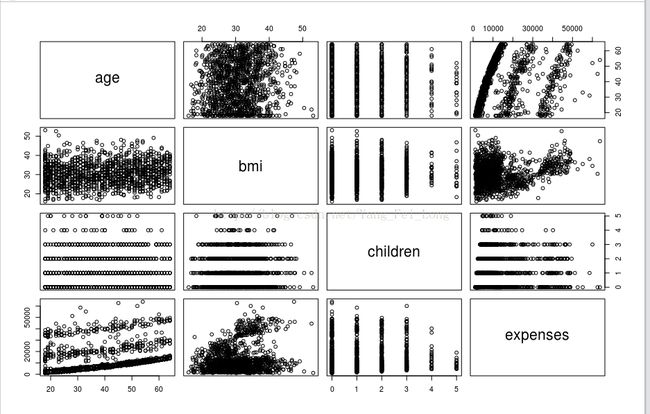
在R中，提供了pairs()方法，通过可视化的方式帮助我们查看两个变量之间的关系。如：

pairs(insurance[c("age", "bmi", "children", "expenses")])

可以有一下效果:

但是，这种图虽然直观，但是表示出的信息量还是有限。有一个优秀的第三包psych，推荐大家使用.再安装并且导入(install.packages("psych"),library(pshch))之后，通过

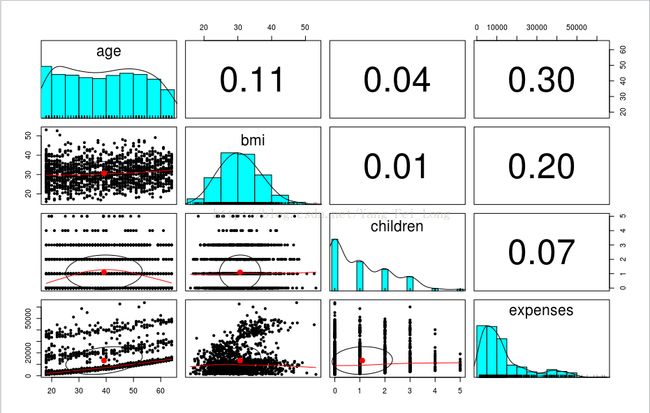
pairs.panels(insurance[c("age","bmi","children","expenses","sexmale")])

可以看到:

从这张图中，我们可以看出age和expenses并非呈现一元线性关系，更像是一条抛物线(图中的红线表示y值在x出的均值)。所以，我们在做线性预测时候，不能简单的预测

expenses=m*age,而是应该为expenses=n*age^2+m*age (m和n都是系数）。

所以预测的模型可以写成:

ins_new_model<-lm(expenses~.+age^2,data = insurance)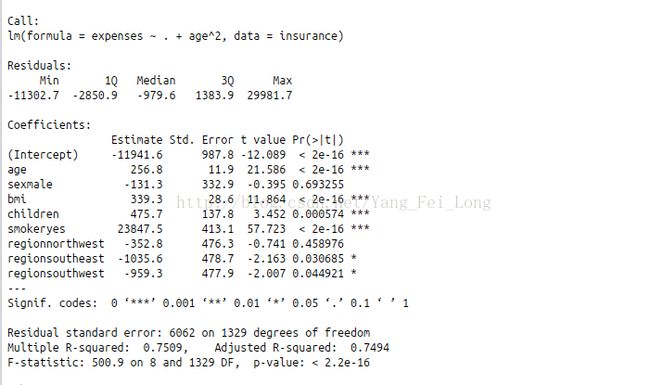

然而对于多元R方值并没有多少变化（毕竟age和expenses并不是那种很强的二次关系，由图可以看出）

另外，结合实际，不仅吸烟也肥胖的人是不是患病率更高？所以，我们可以在肥胖和吸烟之间建立连接关系

首先，在数据源中添加一条额外的判断是否肥胖的属性。（我们姑且将bim>30的人定义为肥胖吧）

insurance$bmi30<-ifelse(insurance$bmi>30,1,0)

然后，在建立模型时表明二者互相成立时的影响

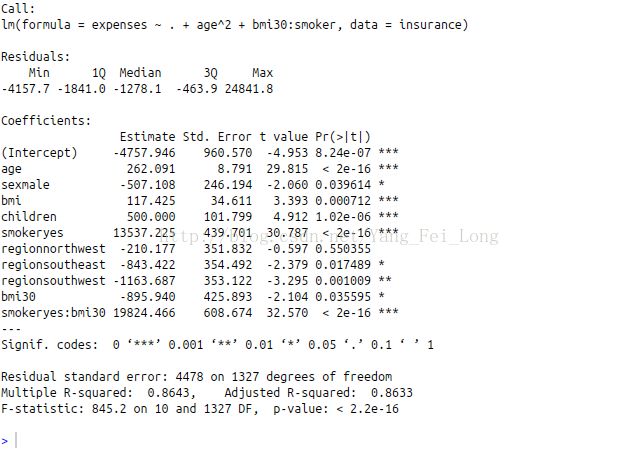
ins_new_model<-lm(expenses~.+age^2+bmi30:smoker,data = insurance)

再次展示结果是：

我们会惊异的发现，多元R方值居然提升到了0.8643,这就意味着成功率已经高达86%,这说明我们的优化是可行的。

但是，在实际中，我们要尽量保证成功能超过90%,所以还有其他方面的优化，就请各位自己考虑了，我就不多做讲述了。^_^

最后，附上数据:

链接: https://pan.baidu.com/s/1miwwcJm 密码: xhb2