论文笔记：KDD 2020 Adaptive Graph Encoder for Attributed Graph Embedding

前言

属性图嵌入，具体来说就是通过图数据结构中的拓扑关系和节点特征信息完成节点表示学习的过程。其中属性图的具体指的就是节点的特征信息。作者首先分析了现有的基于 GCN 的属性图嵌入方法的三个缺点，分别是：

1. 图卷积滤波器与权矩阵的纠缠不仅会影响性能，而且会影响鲁棒性
2. 这些方法中的图卷积滤波器是广义拉普拉斯平滑滤波器的特殊情况，但它们并不保留最优低通特性。
3. 现有算法的训练目标通常是恢复邻接矩阵或特征矩阵（通过自动编码器框架），这与实际应用并不总是一致的。

因此，作者提出了一种自适应的图编码方法 Adaptive Graph Encoder (AGE)。也是一种全新的属性图嵌入框架，AGE 有如下两个特点：

1. 为了更好的缓解由节点特征带来的高频噪声信号，AGE 首次提出利用经过精心设计的拉普拉斯平滑滤波器缓解这一现象。
2. AGE 使用自适应的编码器来迭代的增强滤波特征来更好地完成节点嵌入。

首先从属性图嵌入这一问题出发，就需要考虑两种类型的输入数据：代表数据之间拓扑关系的邻接矩阵、代表节点特征的特征矩阵。相对应这两类信息的代表性操作分别是从邻接矩阵中计算得到的拉普拉斯矩阵，以此作为滤波器对拓扑结构特征进行学习。以及以 MLP 思想为代表的特征变换过程，也就是层与层之间的权重矩阵。

如果想要完成更好的属性图嵌入，关于权重矩阵和图拓扑信号滤波器的纠缠关系就需要进一步的探究，本文就是以此作为出发点，着重探讨了滤波器和权重矩阵的纠缠关系以获得更好的属性图嵌入结果。

论文链接：https://arxiv.org/pdf/2007.01594v1.pdf
github：https://github.com/thunlp/AGE

1. AGE

Adaptive Graph Encoder (AGE)，具体来说是一种属性图的嵌入框架，其中包括一个有效的图滤波器来实现在节点特征上的拉普拉斯平滑，在得到拉普拉斯平滑后的节点特征后，利用一个基于自适应学习的表示学习模块进行进一步处理，最后得到的属性图嵌入结果被用于各类型的下游任务例如节点聚类、连接预测等。

1.1 Problem Formalization

首先给出一个属性图 $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathbf{X})$，其中 $\mathcal{V}=\{v_1,v_2,\dots ,v_n\}$ 代表 $n$ 个节点的集合，$\mathcal{E}$ 代表边的集合，$\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n{]}^T$ 代表特征矩阵。该属性图的拓扑结构特征可以描述为 $\mathbf{A}=\{a_{ij}\}\in {\mathbb{R}}^{n\times n}$。图中节点的度矩阵可以表示为 $\mathbf{D}=diag(d_1,d_2,\dots ,d_n)\in {\mathbb{R}}^{n\times n}$，本文中标准化的拉普拉斯矩阵被定义为 $\mathbf{L}=\mathbf{D}-\mathbf{A}$。

属性图嵌入的最终目的是将图中节点的特征映射为一个低维的特征表示，将 $\mathbf{Z}$ 作为映射后的特征矩阵，并且这个特征矩阵应该包含图 $\mathcal{G}$ 中的拓扑结构特征和特征信息。

具体的下游任务为节点聚类任务和链路预测任务，具体的定义不再介绍。

1.2 Overall Framework

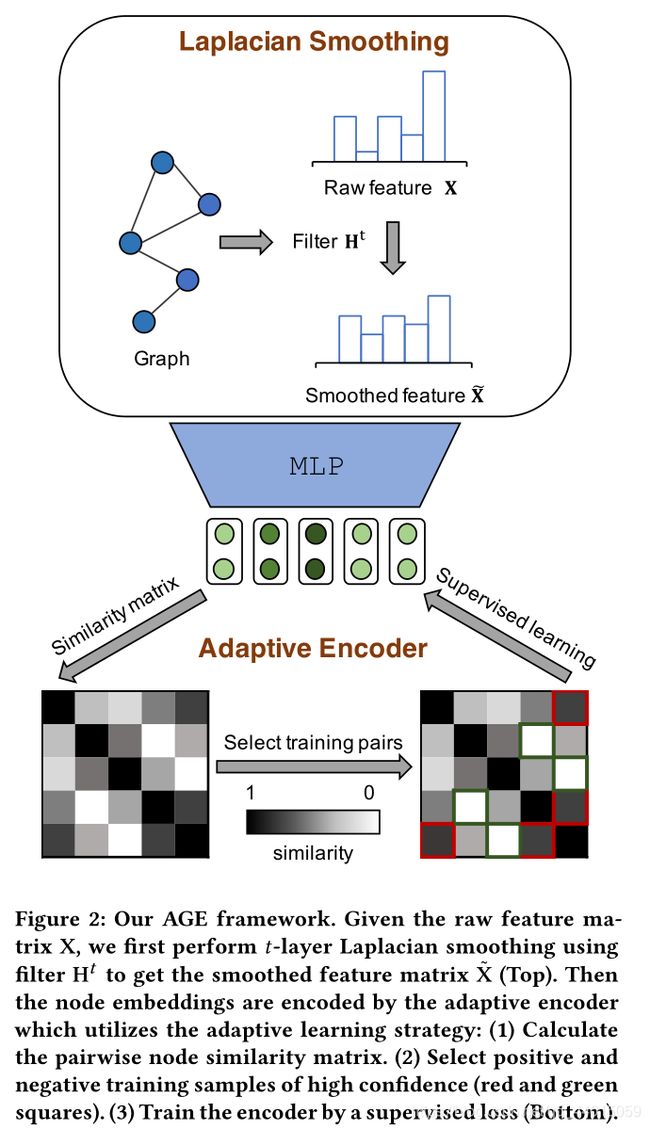
整个模型框架的两个最重要的部分分别为：一个拉普拉斯平滑滤波器和自适应的编码器。

• Laplacian Smoothing Filter ：滤波器 $\mathbf{H}$ 作为低通滤波器去噪特征矩阵 $\mathbf{X}|$ 的高频分量。将平滑后的特征矩阵 $\mathbf{X}$ 作为自适应编码器的输入。
• Adaptive Encoder：为了获得表达能力更强的节点嵌入，这个模块通过自适应选择高度相似或不相似的节点对来构建训练集。然后以监督的方式训练编码器。

通过上述两个过程可以得到嵌入结果的矩阵表示 $\mathbf{Z}$ 被用于各类下游任务。

1.3 Laplacian Smoothing Filter

图学习的基本假设是图上的邻近节点应该是相似的，因此节点特征在图流形上应该是平滑的。

1.3.1 AnalysisofSmoothSignals

从图信号处理的角度开始解释平滑，假设一个图信号可以表示为 $\mathbf{x}\in {\mathbb{R}}^n$ ，其中每个节点都被分配一个标量。假设滤波器矩阵表示为 $\mathbf{H}$。为了度量图信号之间的相似性 ,通过引入 Rayleigh quotient（瑞利商）基于图拉普拉斯矩阵 $\mathbf{L}$ 和特征矩阵 $\mathbf{x}$ 进行计算：
$$R(\mathbf{L},\mathbf{x})=\frac{{\mathbf{x}}^{\mathbf{T}}\mathbf{L}\mathbf{x}}{{\mathbf{x}}^{\mathbf{T}}\mathbf{x}}=\frac{{\sum }_{(i,j)\in \mathcal{E}}(x_i-x_j{)}^2}{{\sum }_{i\in \mathcal{V}}{x}_i^2}\text{\hspace{1em}(1)}$$

这个商实际上是 $\mathbf{x}$ 的标准化方差分数。如上所述，平滑信号应该在邻近节点上分配相似的值。因此，瑞利商较低的信号更平滑。

图的拉普拉斯特征分解可以表示为 $\mathbf{L}=\mathbf{U}\mathbf{\Lambda }{\mathbf{U}}^{-1}$，其中 $\mathbf{U}\in {\mathbb{R}}^{n\times n}$ 是特征向量，$\Lambda =diag({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n)$ 是由特征值组成的对角矩阵，由此来衡量特征向量 ${\mathbf{u}}_i$ 的光滑程度的瑞利商计算公式如下：
$$R(\mathbf{L},{\mathbf{u}}_{\mathbf{i}})=\frac{{\mathbf{u}}_{\mathbf{i}}^{\mathbf{T}}\mathbf{L}{\mathbf{u}}_{\mathbf{i}}}{{\mathbf{u}}_{\mathbf{i}}^{\mathbf{T}}{\mathbf{u}}_{\mathbf{i}}}={\lambda }_i\text{\hspace{1em}(2)}$$

上式表明平滑的特征向量与更小的特征值相关，这意味着更低的频率。也就是说特征向量的平滑程度与特征值大小相关，如果特征值较低那么特征向量的频率更低，更平滑。

基于此可以在 $\mathbf{L}$ 的基础上对图信号 $\mathbf{x}$ 进行分解：
$$\mathbf{x}=\mathbf{U}\mathbf{p}=\sum _{i=1}^n{p}_i{\mathbf{u}}_i\text{\hspace{1em}(3)}$$

其中 $p_i$ 代表特征向量 ${\mathbf{u}}_i$ 的系数，则图信号的平滑程度最终表示为：
$$R(\mathbf{L},\mathbf{x})=\frac{{\mathbf{x}}^{\mathbf{T}}\mathbf{L}\mathbf{x}}{{\mathbf{x}}^{\mathbf{T}}\mathbf{x}}=\frac{{\sum }_{i=1}^n{p}_i^2{\lambda }_i}{{\sum }_{i=1}^n{p}_i^2}\text{\hspace{1em}(4)}$$

因此，为了得到更平滑的信号，滤波器的目标是在保留低频分量的同时对高频分量进行滤波。由于高计算效率和令人信服的性能，拉普拉斯平滑滤波器经常被用于这一目的。

1.3.2 Generalized Laplacian Smoothing Filter

一般形式下的拉普拉斯平滑滤波器可以被定义为：
$$\mathbf{H}=\mathbf{I}-k\mathbf{L}\text{\hspace{1em}(5)}$$
其中，$k$ 是实数。采用 $\mathbf{H}$ 作为滤波矩阵，滤波信号 $x$ 经过拉普拉斯平滑滤波器的结果如下表示：
$$\mathbf{x}=\mathbf{H}\mathbf{x}=\mathbf{U}(\mathbf{I}-k\mathbf{\Lambda }){\mathbf{U}}^{-1}\mathbf{U}\mathbf{p}=\sum _{i=1}^n(1-k{\lambda }_i)p_i{\mathbf{u}}_i=\sum _{i=1}^n{p}_i^{\prime }{\mathbf{u}}_i\text{\hspace{1em}(6)}$$

这里所指的 $\mathbf{x}$ 并不是节点特征，而是由拉普拉斯矩阵所代表的图拓扑结构特征，是从拓扑结构角度来定义的图信号，用于解释一般条件下的图拉普拉斯平滑滤波器。

通过上述过程，说明了拉普拉斯平滑滤波器对于拓扑结构特征信号的处理，由此就可以推广到以节点特征矩阵作为图信号的形式，也是实际的属性图聚类中的形式。

因此，为了实现低通滤波，频响函数$1-k\lambda$ 应该是一个衰减的非负函数。叠加 $t$ 个拉普拉斯平滑滤波器，滤波后的特征矩阵可以表示为：
$$\mathbf{X}={\mathbf{H}}^t\mathbf{X}\text{\hspace{1em}(7)}$$

滤波器 ${\mathbf{H}}^t$ 的计算不包含任何参数

1.3.3 The Choice of k

基于加上自环的邻接矩阵 $\mathbf{A}=\mathbf{I}+\mathbf{A}$，利用对称归一化的技巧得到处理后的拉普拉斯矩阵的过程如下：
$${\mathbf{L}}_{sym}={\mathbf{D}}^{-\frac{1}{2}}\mathbf{L}{\mathbf{D}}^{-\frac{1}{2}}\text{\hspace{1em}(8)}$$
基于上述过程，卷积核变为：
$$\mathbf{H}=\mathbf{I}-k{\mathbf{L}}_{sym}\text{\hspace{1em}(9)}$$
当 $k=1$ 的时候就是 GCN 的卷积核

对于参数 $k$ 的选择，应该考虑特征值 $\Lambda$ 的分布，对于经过滤波器处理后的信号的平滑程度度量为：
$$R(\mathbf{L},\mathbf{x})=\frac{{\mathbf{x}}^{\mathbf{T}}\mathbf{L}\mathbf{x}}{{\mathbf{x}}^{\mathbf{T}}\mathbf{x}}=\frac{{\sum }_{i=1}^n{p}_i^{{}^{\prime }2}{\lambda }_i}{{\sum }_{i=1}^n{p}_i^{{}^{\prime }2}}\text{\hspace{1em}(10)}$$

因此 $p_i^{{}^{\prime }2}$ 应该随着 ${\lambda }_i$ 的增加而减少。因为随着特征值的增大，特征向量的系数会随之减小。假定特征值中的最大值为 ${\lambda }_{max}$，从理论上讲

• 当 $k>1/{\lambda }_{max}$ 时，代表滤波器不是一个低通滤波器，因为 $p_i^{{}^{\prime }2}$ 在这个区间内增加。
• 当 $k<1/{\lambda }_{max}$ 时，这个滤波器不能使所有的高频成分去噪。
• 因此当 $k=1/{\lambda }_{max}$ 时是最适合的情况。

对于不同的数据集来说，特征值的最大值是不同的。

1.4 Adaptive Encoder

通过 $t$ 层拉普拉斯平滑滤波，输出特征更加平滑，并保留了丰富的属性信息。

为了从平滑的特征中学习到更好的节点嵌入，需要找到一个合适的无监督优化目标。在属性图嵌入任务中，两个节点之间的关系至关重要，这就要求训练目标具有合适的相似性度量。作者认为邻接矩阵只记录单跳结构信息是不够的。因此，作者自适应选择相似度高的节点对作为正样本，相似度低的节点对作为负样本。

给定滤波后的节点特征 $\mathbf{X}$，节点嵌入采用线性编码器 $f$ 进行编码:

$$\mathbf{Z}=\mathbf{f}(\mathbf{X};\mathbf{W})=\mathbf{X}\mathbf{W}\text{\hspace{1em}(11)}$$

其中 $\mathbf{W}$ 是可训练的权重矩阵。通过最小-最大标量将嵌入缩放到 [0,1] 区间以减少方差。为了测量节点的两两相似度，利用余弦函数来实现相似度度量。相似矩阵 $\mathbf{S}$ 表示如下：
$$\mathbf{S}=\frac{\mathbf{Z}{\mathbf{Z}}^{\mathbf{T}}}{||\mathbf{Z}|{|}_2^2}\text{\hspace{1em}(12)}$$

1.4.1 Training Sample Selection

在计算相似矩阵后，将两两相似序列按降序排序。这里 $r_{ij}$ 是节点对 $(v_i,v_j)$ 的分数。将正样本的最大分数设为 $r_{pos}$ ，负样本的最小秩设为 $r_{neg}$。因此，生成的节点对 $(v_i,v_j)$ 的标签为

$$f(x)=\{\begin{array}{llc}1& =& r_{ij}\le r_{pos}\\ 0& =& r_{ij}\ge r_{pos}\\ None& =& otherwise\end{array}\text{\hspace{1em}(13)}$$

这样，构造了一个包含 $r_{pos}$ 个正样本和 $n^2-r_{neg}$ 个负样本的训练集。在第一次构造训练集时，由于编码器没有被训练，直接使用平滑的特征来初始化 $\mathbf{S}$:
$$\mathbf{S}=\frac{\mathbf{X}{\mathbf{X}}^{\mathbf{T}}}{||\mathbf{X}|{|}_2^2}\text{\hspace{1em}(14)}$$

构造好训练集后，可以用监督的方式训练编码器。在真实世界的图中，不相似的节点对总是远远多于正节点对，因此在训练集中选择多于 $r_{pos}$ 个负样本。为了平衡正/负样本，在每次迭代中随机选择 $r_{pos}$ 个负样本。平衡训练集用 $\mathcal{O}$ 表示。因此，交叉熵损失表示如下：
$$\mathcal{L}=\sum _{v_i,v_j\in \mathcal{O}}-l_{ij}log(s_{ij})-(1-l_{ij})log(1-s_{ij})\text{\hspace{1em}(15)}$$

1.4.2 Thresholds Update

训练过程中，作者设计了一种针对 $r_{pos}$ 和 $r_{neg}$ 的具体更新策略，以控制训练集的大小。在训练过程的开始，选择更多的样本用于编码器，以发现粗糙的聚类模式。在此之后，保留具有较高置信度的样本进行训练，迫使编码器捕获精炼的模式。实际中，随着训练过程的进行，$r_{pos}$ 呈线性下降，$r_{neg}$ 呈线性增加。初始的阈值分别为 $r_{pos}^{st}$ 和 $r_{neg}^{st}$。最终的阈值为 $r_{pos}^{ed}$ 和 $r_{neg}^{ed}$，其中满足 $r_{pos}^{ed}\le r_{pos}^{st}$ 和 $r_{neg}^{ed}\ge r_{neg}^{st}$。其中阈值更新 $T$ 次的策略为：
$$r_{pos}^{\prime }=r_{pos}+\frac{r_{pos}^{ed}-r_{pos}^{st}}{T}\text{\hspace{1em}(16)}$$
$$r_{neg}^{\prime }=r_{neg}+\frac{r_{neg}^{ed}-r_{neg}^{st}}{T}\text{\hspace{1em}(17)}$$

随着训练过程的进行，每次更新阈值时重构训练集并保存嵌入信息。在节点聚类方面，对保存的嵌入相似度矩阵进行谱聚类，并通过 (DBI) 指数来选择最佳的迭代次数，该指数在没有标注信息的情况下衡量聚类质量。对于链路预测，在验证集上选择性能最好的迭代次数。

2. Experiments