【阅读笔记 EMNLP2020】《Message Passing for Hyper-Relational Knowledge Graphs》

题目：Message Passing for Hyper-Relational Knowledge Graphs（超关系知识图谱的知识传递）
会议：EMNLP2020
论文地址：
https://arxiv.org/abs/2009.10847(arxiv)
https://www.researchgate.net/publication/344359783_Message_Passing_for_Hyper-Relational_Knowledge_Graphs(reaseearchgate)
代码地址：
https://github.com/migalkin/StarE
其他：出自德国德累斯顿工业大学和弗劳恩霍夫应用研究促进协会

这个是Jens Lehmann组的成果，曾发表过《DBpedia: A nucleus for a web of open data》（获得近五千引用）。

目录

1. 超关系知识图谱（Hyper-relational knowledge graph）
2. 链接预测（link prediction）
2.1 三元关系推断（triple-relation link prediction）
2.2 多元关系推断（multi-relation link prediction）
3. 相关工作
4. 前备知识
4.1 基于无向图的图神经网络模型
4.2 基于无向图的图神经网络模型
4.3 超关系图
5. 动机
6. STARE
7. WD50K Dataset
8. 实验
9. 结论
10. 疑问汇总

---

1. 超关系知识图谱（Hyper-relational knowledge graph）

超关系的知识图谱是指由多个多元关系事件构成的知识图谱，每个多元关系事件可以由一个三元组+n个附加键值对附加信息表示。超关系知识图谱可以有效的结构化表示多元关系，有助于下一步对其进行编码分析。

2. 链接预测（link prediction）

自2016起，知识图谱方向逐渐升温，吸引了一批又一批学者的兴趣。经典的知识图谱任务有图谱表示、图谱融合、链接预测、节点预测等。在我们这篇文章中，主要介绍近年来链接预测的发展情况，并分析EMNLP2020的一篇工作《Message Passing for Hyper-Relational Knowledge Graphs》。
链接预测任务是指，基于目前图谱中已有的links，推断出新的links，其中包括entity prediction和relation prediction。

2.1 三元关系推断（triple-relation link prediction）

目前，大多数的link predict方法是基于由三元组构成的知识图谱，预测的目标是一个relation是否可以将两个entities连接起来，或者给定一个relation、一个entity，推断一个entity，使其构成一个新的三元组。

2.2多元关系推断（multi-relation link prediction）

但是由于三元组具有严格的形式化要求，必须是一个relation连接两个entities，往往不能很好表示facts，特别是对于一些还有辅助信息的facts。如下所示，三元关系推断可以很好的表示图中A部分的fact，爱因斯坦曾就读于苏黎世联邦理工学院、爱因斯坦曾就读于苏黎世大学。但是无法很好的表示图中B部分的fact，爱因斯坦在苏黎世联邦理工学院学习数学，获得学士学位，在苏黎世大学学习物理，获得博士学位。

但可以使用多元关系很好的表示B部分的fact，我们可以将一个fact表示为，s、r、o分别表示头实体、关系、尾实体，s、r、o构成主三元组，如图B中的、，Q为辅助信息，如B图中的、、、。这样，我们就可以准确的描述一个fact。

3. 相关工作

早期图表示方法会过分的简化辅助信息，如m-TransH将一个多元关系转换为多个三元关系，RAE、HypE等模型将多元关系中主三元组中的关系以及辅助信息中的键，抽象为一个新的关系。

最近，对多元关系的研究主要分为两个方向：

1. 将多元关系简化为多个三元关系，如GETD、TuckER；
2. 使用新的范式表示多元关系，如NaLP使用多个键值对表示多元关系、HINGE和NeuInfer使用主三元组+辅助信息的形式表示多元关系。

4. 前备知识

4.1 基于无向图的图神经网络模型

无向图可以形式化为$G=(\Gamma ,\xi )$， 其中$\Gamma$表示结点集合，$\xi$表示边的集合，每一个点$\gamma \in \Gamma$都有相对应的表示向量${\mathbf{h}}_{\gamma }$和邻居结点$N(\gamma )$。
2017年Gilmer et al.提出的信息传递的框架为
$${\mathbf{h}}_v^{k+1}=UDP({\mathbf{h}}_v^k,\underset{u\in N(\gamma )}{\mathrm{AGGN}}\varphi ({\mathbf{h}}_{\gamma }^k,{\mathbf{h}}_u^k,e_{\gamma u}))$$
$AGGR(\cdot )$、$UPD(\cdot )$分别是邻居聚合、结点更新的函数，${\mathbf{h}}_{\gamma }^k$是第$k$层结点$\gamma$的表示，${\mathbf{e}}_{\gamma u}$是结点$\gamma 、u$之间的连边的表示。
不同的图编码模型使用不同的邻居聚合、结点更新的策略。例如Kipf和Welling2017年提出的GCN模型，结点通过使用一个权重矩阵聚合邻居结点，并通过一个激活函数，比如$ReLU$，得到新的表示。GCN上第$k$层结点$\gamma$可以表示为
$${\mathbf{h}}_{\gamma }^k=f(\sum _{u\in N(\gamma )}{\mathbf{W}}^k{\mathbf{h}}_u^{k-1})$$
但是，以上模型存在明显的不足，GCN和其他相似的结构不能编码含不同关系的表示，这要求提出支持多关系的图谱表示学习。

4.2 基于有向图的图神经网络模型

在多关系的图谱表示学习中，有向图可以表示为$G=(\Gamma ,R,\xi )$，$R$表示关系集合，$\xi$表示有向边$(s,r,o)$的集合，$s\in \Gamma$、$o\in \Gamma$，$s、o$通过关系$r\in R$连接起来。
GCN模型假设关系是单向的，因此往往会将逆边$(o,r^{-1},s)$加入到数据集$\xi$中。且对于每一结点都会加入它的自环$(\gamma ,r^{self},\gamma )$，以此在邻居聚合、更新节点中保留结点本身的信息。
对于有向图编码，Schlichtkrull et al.提出R-GCN，使用多个权重矩阵${\mathbf{W}}_r$表示不同的关系$r$，以此来进行多关系的聚合。
$${\mathbf{h}}_{\gamma }^k=f(\sum _{(u,r)\in N(\gamma )}{\mathbf{W}}_r^k{\mathbf{h}}_u^{k-1})$$

但是上述的模型在实验时往往会面对参数爆炸，因此Vashishth et al.提出 CompGCN，使用基向量分解。
$${\mathbf{h}}_{\gamma }^k=f(\sum _{(u,r)\in N(\gamma )}{W}_{\lambda (\gamma )}^k\varphi ({\mathbf{h}}_u^{k-1},h_{\gamma }^{k-1}))$$
$\varphi (\cdot )$是组合操作，包含相加、相减等操作，${\mathbf{W}}_{\lambda (\gamma )}$为方向向量权重矩阵，包含正向、反向、逆等关系。

4.3超关系图

一个超关系图，可以表示为$G=(\Gamma ,R,\xi )$，$\xi$是边的集合$e_1,...,e_n$，$e_j\in \Gamma \times R\times \Gamma \times P(R\times \Gamma )$，$e_j$表示超关系，$e_j$通常可以表示为$(s,r,o,Q)$，$Q$是辅助信息的集合，按照这种方式2.2中的图B可以表示为(Albert Einstein, educated at, University of Zurich, (academic degree, Doctorate), (academic major, Physics))。

5. 动机

但是以上模型都具有明显不足：

1. 无法编码含任意数量的辅助信息的fact；
2. 辅助信息与主三元组之间的交互仍存在问题，比如辅助信息之间交互、主三元组与不同辅助信息交互时，每次仅考虑一个fact没有综合学习相关fact。

出于以上原因，作者提出了一种图网络模型——STARE，首次使用图神经网络进行多元关系预测任务。

6. STARE

STARE的模型图如下所示。

废话不多说，直接上公式。
$${\mathbf{h}}_{\gamma }=f(\sum _{(u,r)\in N(\gamma )}{\mathbf{W}}_{\lambda (r)}{\varphi }_r({\mathbf{h}}_u,\gamma ({\mathbf{h}}_r,{\mathbf{h}}_q{)}_{vu}))$$
首先使用${\varphi }_q$聚合辅助信息的键值对，然后对所有辅助信息进行汇总，通过一个权重矩阵${\mathbf{W}}_q$转换到主三元组空间，将其与主三元组的关系进行加权组合，将其得到向量与尾实体进行组合后投影到头实体，最终聚合后得到头实体表示。

聚合辅助信息如下述所示。
$$\gamma ({\mathbf{h}}_r,{\mathbf{h}}_q)=\alpha ⨀{\mathbf{h}}_r+(1-\alpha )⨀{\mathbf{h}}_q$$

$${\mathbf{h}}_q={\mathbf{W}}_q\sum _{(qr,rv)\in Q_{j{r}_{vu}}}{\varphi }_q({\mathbf{h}}_{qr},{\mathbf{h}}_{qv})$$
公式比较好理解，不再过多赘述。

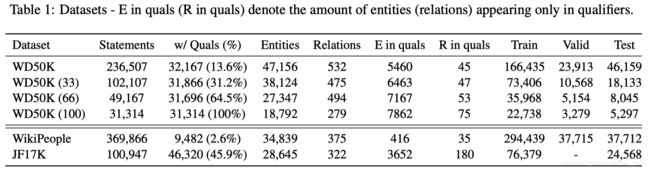
7. WD50K Dataset

多元关系推断常用数据集有JF17K和WikiPeople，作者讨论了这两个数据集的不足之处。

1. WIkiPeople数据集含有大量数字结点，如时间等，这部分信息往往是可以被忽略掉的，去掉后仅有3%的数据为超关系事件
2. JF17K数据集存在数据泄漏问题，在测试集中44.5%的主三元组已经出现在了训练集中

因此，作者基于Wikidata提出了一个新的数据集WD50K，不存在以上两种问题，并对其构建了多个变体，WD50K（33）等。括号中的数字表示超关系事件对所占的比例。

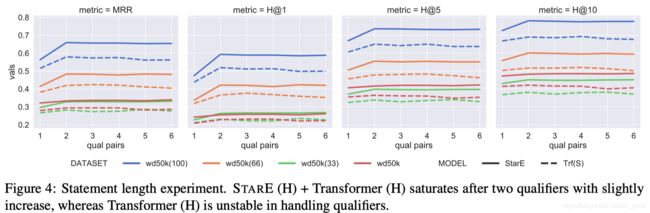
8. 实验

文章主要的工作在于STARE图结构编码超关系事件、提出新的数据集WD50K，在实验部分，模型的解码器使用Transformer。

上述两个表分别展示了STARE在WIkiPeople、JF17K和WD50K上的试验结果，试验结果挺不错哒：）
并且作者单独分析了模型对超关系数据的影响以及transformer对试验结果的影响，证明模型确实可以有效编码超关系数据，transformer可以降低过拟合。

作者同时对比了模型在对JF17K原始数据集与清洁后的数据集的结果。

9. 总结

本文主要介绍了超关系知识图谱的关系推断，包括三元关系推断、多元关系推断，然后介绍了EMNLP2020的一篇文章《Message Passing for Hyper-Relational Knowledge Graphs》，该文章首次将图网络应用于多元关系推断任务，并重新构建了一个数据集。

10. 疑问汇总

1. 文章中提出的STRAE模型结构仍存在一定问题，为什么将辅助信息与主三元组的关系进行组合？而不是主三元组整体？
2. 文章中批评了WikiPeople数据集包含太多数字信息，重构了WD50K数据集，数字信息难道不重要吗？