感知器与BP神经网络学习笔记

（一）感知器
1.1 基本介绍
感知器学习算法是神经网络中的一个概念，单层感知器是最简单的神经网络，输入层和输出层直接相 连，每一个输入端和其上的权值相乘，然后将这些乘积相加得到乘积和，这个结果与阈值相比较（一般为0），若大于阈值输出端就取1，反之，输出端取-1

1.2 感知器分类算法步骤
权重向量W，训练样本X
1.把权重向量初始化为0，或把每个分类初始化为[0,1]间任意小数
2.把训练样本输入感知器，得到分类结果（1或-1）
3.根据分类结果更新权重向量
.
1.3权重更新算法
W(j)=W(j)+ΔW(j)；ΔW(j)=η*(y-y’)*X(j)；
η：表示学习率，是介于[0,1]之间 的一个小数
y：输入样本的正确分类
y’：感知器计算出来的分类
通过上面公式不断更新权值，直到达到分类要求。
.
1.4 代码实现

% 1. 感知器神经网络的构建
% 1.1  生成网络
net=newp([0 2],1);%单输入，输入值为[0,2]之间的数
inputweights=net.inputweights{1,1};%第一层的权重为1
biases=net.biases{1};%阈值为1
% 1.2  网络仿真

net=newp([-2 2;-2 2],1);%两个输入，一个神经元，默认二值激活
net.IW{1,1}=[-1 1];%权重，net.IW{i,j}表示第i层网络第j个神经元的权重向量
net.IW{1,1}
net.b{1}=1;
net.b{1}
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] [1 ;-1]},a3=sim(net,p3) %两组数据放一起
p4=[1 1;1 -1],a4=sim(net,p4)%也可以放在矩阵里面
net.IW{1,1}=[3,4];
net.b{1}=[1];
a1=sim(net,p1)
% 1.3  网络初始化
net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
% 改变权值和阈值为随机数
net.inputweights{1,1}.initFcn='rands';
net.biases{1}.initFcn='rands';
net=init(net);
bias=net.b{1}
wts=net.IW{1,1}
a1=sim(net,p1)

% 2. 感知器神经网络的学习和训练
% 1 网络学习
net=newp([-2 2;-2 2],1);
net.b{1}=[0];
w=[1 -0.8]
net.IW{1,1}=w;
p=[1;2];
t=[1];
a=sim(net,p)
e=t-a
help learnp
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)


net = newp([0 1; -2 2],1);
P = [0 0 1 1; 0 1 0 1];
T = [0 1 1 1];
Y = sim(net,P)
net.trainParam.epochs = 20;
net = train(net,P,T);
Y = sim(net,P)


% 2 网络训练
net=init(net);
p1=[2;2];t1=0;p2=[1;-2];t2=1;p3=[-2;2];t3=0;p4=[-1;1];t4=1;
net.trainParam.epochs=1;
net=train(net,p1,t1)
w=net.IW{1,1}
b=net.b{1}
a=sim(net,p1)
net=init(net);
p=[[2;2] [1;-2] [-2;2] [-1;1]];
t=[0 1 0 1];
net.trainParam.epochs=1;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=2;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=20;
net=train(net,p,t);
a=sim(net,p)

% 3. 二输入感知器分类可视化问题
P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];
T=[1 1 0 1]
net=newp([-1 1;-1 1],1);
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1});
%hold on;
%plotpv(P,T);
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1})
net.adaptParam.passes=3;
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpc(net.IW{1},net.b{1})
net.adaptParam.passes=6;
net=adapt(net,P,T)
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1},net.b{1})

plotpc(net.IW{1},net.b{1})
%仿真
a=sim(net,p);
plotpv(p,a)

p=[0.7;1.2]
a=sim(net,p);
plotpv(p,a);
hold on;
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
%感知器能够正确分类，从而网络可行。

% 4. 标准化学习规则训练奇异样本
P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50]
T=[1 1 0 0 1];
net=newp([-40 1;-1 50],1);
plotpv(P,T);%标出所有点
hold on;
linehandle=plotpc(net.IW{1},net.b{1});%画出分类线
E=1;
net.adaptParam.passes=3;%passes决定在训练过程中训练值重复的次数。
while (sse(E))
    [net,Y,E]=adapt(net,P,T);
    linehandle=plotpc(net.IW{1},net.b{1},linehandle);
    drawnow;
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%另外一种网络修正学习（非标准化学习规则learnp）
hold off;
net=init(net);
net.adaptParam.passes=3;
net=adapt(net,P,T);
plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%无法正确分类
%标准化学习规则网络训练速度要快！

% 训练奇异样本
% 用标准化感知器学习规则（标准化学习数learnpn）进行分类
net=newp([-40 1;-1 50],1,'hardlim','learnpn');
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net.adaptParam.passes=3;
net=init(net);
linehandle=plotpc(net.IW{1},net.b{1});
while (sse(e))
[net,Y,e]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
end;
axis([-2 2 -2 2]);
net.IW{1}%权重
net.b{1}%阈值
%正确分类

 %非标准化感知器学习规则训练奇异样本的结果
net=newp([-40 1;-1 50],1);
net.trainParam.epochs=30;
net=train(net,P,T);
pause;
linehandle=plotpc(net.IW{1},net.b{1});
hold on;
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);

% 5. 设计多个感知器神经元解决分类问题
p=[1.0 1.2 2.0 -0.8; 2.0 0.9 -0.5 0.7]
t=[1 1 0 1;0 1 1 0]
plotpv(p,t);
hold on;
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net=init(net);
while (sse(e))
[net,y,e]=adapt(net,p,t);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;

1.5 运行结果

样本分类结果图

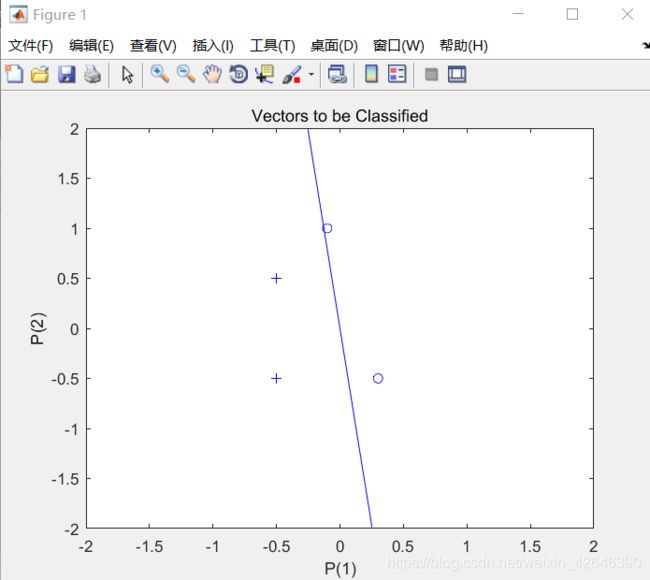
感知器算法结果分析图

训练数据的梯度和均方误差之间的关系图

1.6 部分函数说明
newp函数
作用：构造感知器模型。
句法：net=newp[PR,S,TF,LF]
解释：PR:R*2的输入向量最大值和最小值构成的矩阵，即每一行的最大值最 小值构成一行。
S：构造的神经元的个数
TF：激活函数的设置，可设置为hardlim函数或者hardlins函数，默认为 hardlim函数
LF：学习修正函数的设置，可设置为learnp函数或者learnpn函数，默认 为learnp函数

adapt函数：自适应训练函数
sim函数：对模型进行仿真
plotpc函数：在感知器向量中绘制分界线
plotpv函数： 绘制感知器的输入向量和目标向量

（二）BP神经网络
2.1.概述
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。大家应该对基本的神经网络模型有一定程度的了解，神经网络模型包含了很多神经元模型，每一个神经元都有着自己的权重，然后一般来说，典型的神经网路包含输入层，隐藏层和输出层，然后输入层和隐藏层一般来说都会有自己的偏置项。

2.2代码实现

% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}

p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}

net.IW{1}
net.IW{2}
0.7616+net.b{2}
a-net.b{2}
(a-net.b{2})/ 0.7616
help purelin

p1=[0;0];
a5=sim(net,p1)
net.b{2}
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}




P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,'purelin');
net2=newp([0 2;0 2;0 2;0 2],1,'logsig');
net3=newp([0 2;0 2;0 2;0 2],1,'tansig');
net4=newp([0 2;0 2;0 2;0 2],1,'hardlim');

net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}


net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;

a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)

init(net1);
net1.b{1}

help tansig

% 训练
p=[-0.1 0.5]
t=[-0.3 0.4]
w_range=-2:0.4:2;
b_range=-2:0.4:2;

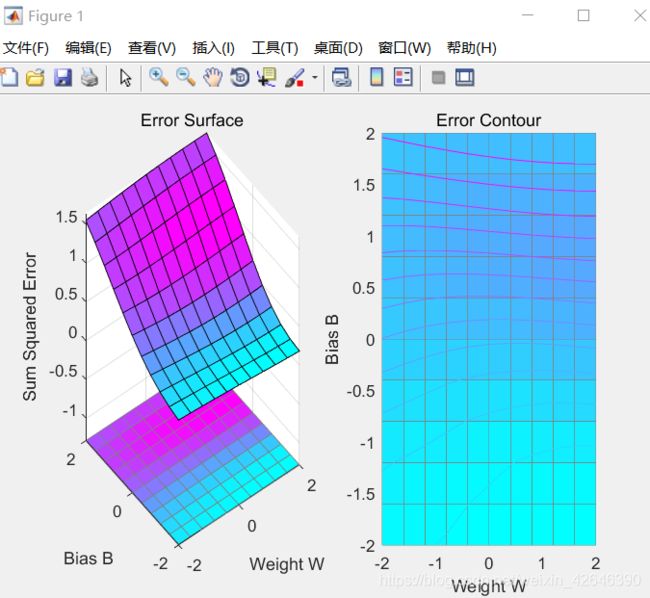
ES=errsurf(p,t,w_range,b_range,'logsig');%单输入神经元的误差曲面
plotes(w_range,b_range,ES)%绘制单输入神经元的误差曲面
pause(0.5);
hold off;
net=newp([-2,2],1,'logsig');
net.trainparam.epochs=100;
net.trainparam.goal=0.001;
figure(2);
[net,tr]=train(net,p,t);
title('动态逼近')
wight=net.iw{1}
bias=net.b
pause;
close;
% 练
p=[-0.2 0.2 0.3 0.4]
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{'tansig','purelin'},'trainlm');
net.trainparam.epochs=100;
net.trainparam.goal=0.0001;
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,'*');
title('样本')
title('样本');
xlabel('Input');
ylabel('Output');
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);
a2=sim(net,ptest2);

net.iw{1}
net.iw{2}
net.b{1}
net.b{2}

3.运行结果


样本绘图结果



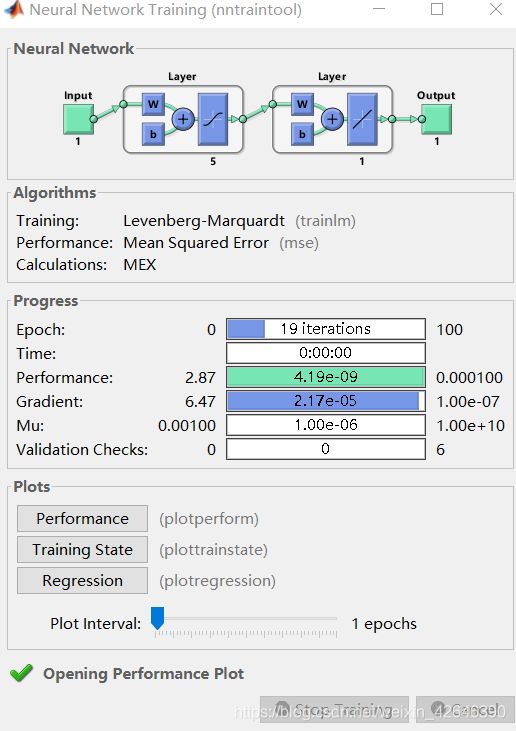
BP神经网络性能图

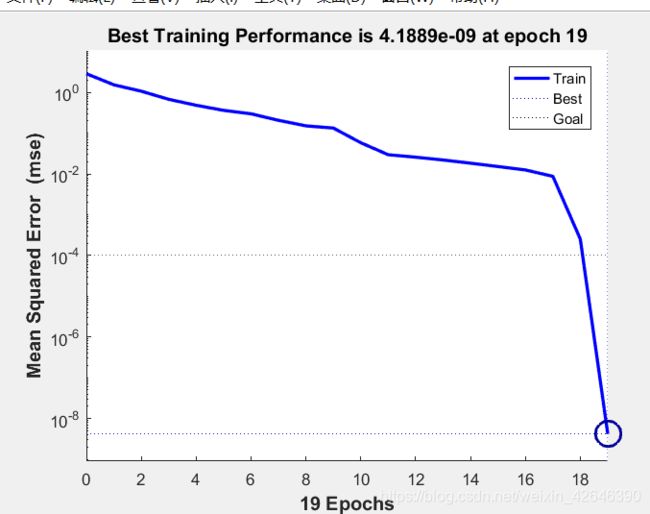
训练状态图

回归分析结果图

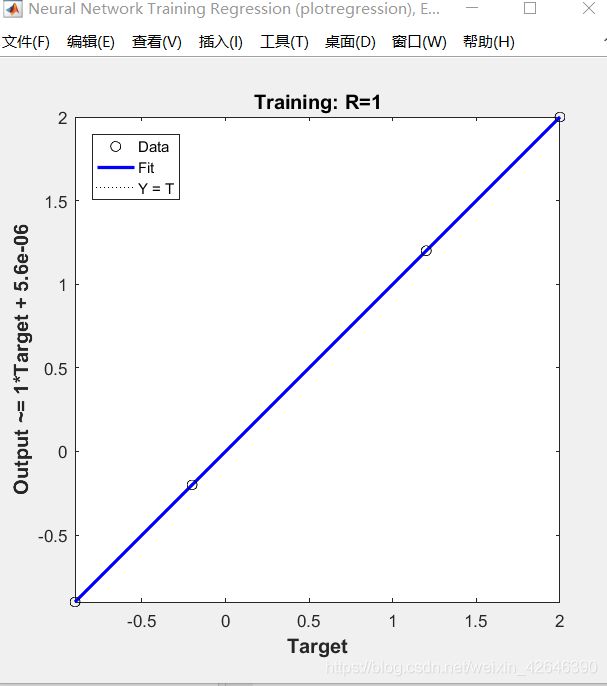
2.3.部分函数说明
newff函数
功能：建立一个前馈反向传播（BP）网络
句法1：net=newff（P,T,S）
P: 输入数据矩阵。(RxQ1)中Q1代表R元的输入向量。其数据意义是矩阵P有Q1列，每一列都是一个样本，而每个样本有R个属性（特征）。一般矩阵P需要事先归一化好，即P的每一行都归一化到[0 1]或者[-1 1]。
T：目标数据矩阵。(SNxQ2)，其中Q2代表SN元的目标向量。
S：第i层的神经元个数。（可以省略输出层的神经元个数不写，因为输出层的神经元个数已经取决于T）

​ 句法2：net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)（提供了可选择的参数）
TF：相关层的传递函数，默认隐含层使用tansig函数，输出层使用purelin函数。
BTF：BP神经网络学习训练函数，默认值为trainlm函数。
BLF：权重学习函数，默认值为learngdm。
PF：性能函数，默认值为mse。
PF，OPF，DDF均为默认值即可。
常用的传递函数:
purelin：线性传递函数
tansig：正切 S 型传递函数
logsig： 对数 S 型传递函数
(ps：隐含层和输出层函数的选择对BP神经网络预测精度有较大影响，一般隐含层节点传递函数选用tansig函数或logsig函数，输出层节点转移函数选用tansig函数或purelin函数。）

train函数
功能：训练一个神经网络(我们这里使用的是梯度下降算法)
句法：[net2,tr] = train(net1,X,T)
net1：待训练的网络
X: 输入数据矩阵
T：目标数据矩阵
net2：训练得到的网络tr：存放有关训练过程的数据的结构体