U-Net: Convolutional Networks for Biomedical Image Segmentation
Abstract
人们普遍认为,成功训练深度网络需要数千个带注释的训练样本。在本文中,我们提出了一种网络和训练策略,该策略依赖于数据增强的强大使用来更有效地使用可用的注释样本。该架构由一个用于捕获上下文的收缩路径和一个能够实现精确定位的对称扩展路径组成。我们表明,这样的网络可以从很少的图像进行端到端训练,并且在ISBI挑战赛中优于先前的最佳方法(滑动窗口卷积网络),用于分割电子显微镜堆栈中的神经元结构。使用在透射光显微镜图像(相差和DIC)上训练的相同网络,我们在这些类别中大幅赢得了2015年ISBI细胞跟踪挑战赛。此外,网络速度很快。在最近的GPU上分割512x512图像只需不到一秒的时间。完整的实现(基于Caffe)和经过训练的网络可在http://lmb.informatik.uni-freiburg.de/people/ronneber/u-net获得。
1 Introduction
在过去的两年里,深度卷积网络在许多视觉识别任务中的表现都超过了最先进的水平,例如[7,3]。虽然卷积网络已经存在了很长时间[8],但由于可用训练集的大小和所考虑网络的大小,它们的成功受到限制。 Krizhevsky等人[7]的突破是由于在具有100万张训练图像的ImageNet数据集上对具有8层和数百万个参数的大型网络进行监督训练。从那时起,已经训练了更大更深的网络[12]。
卷积网络的典型用途是分类任务,其中图像的输出是单个类标签。然而,在许多视觉任务中,尤其是在生物医学图像处理中,所需的输出应该包括定位,即应该为每个像素分配一个类标签。此外,数以千计的训练图像在生物医学任务中通常是遥不可及的。因此,Ciresan等人[1]在滑动窗口设置中训练了一个网络,通过在该像素周围提供一个局部区域(patch)来预测每个像素的类别标签作为输入。首先,这个网络可以局部化。其次,就patch而言,训练数据远大于训练图像的数量。由此产生的网络在ISBI 2012的EM分割挑战中大获全胜。
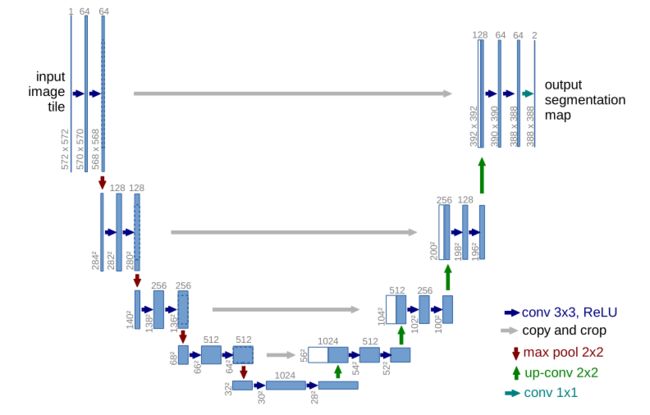
图 1. U-net架构(最低分辨率下的32x32像素示例)。每个蓝色框对应一个多通道特征图。通道数显示在框的顶部。 x-y-size位于框的左下边缘。白框代表复制的特征图。箭头表示不同的操作。
显然,Ciresan 等人 [1] 的策略有两个缺点。首先,它非常慢,因为每个patch都必须单独运行网络,并且由于patch重叠而存在大量冗余。其次,在定位准确性和上下文使用之间存在权衡。较大的patch需要更多的最大池层,这会降低定位精度,而小patch允许网络只能看到很少的上下文。最近的方法[11,4]提出了一个分类器输出,它考虑了来自多个层的特征。良好的本地化和上下文的使用是可能的。
在本文中,我们建立在一个更优雅的架构上,即所谓的“全卷积网络”[9]。我们修改和扩展了这种架构,使其适用于很少的训练图像并产生更精确的分割;参见图1。[9]中的主要思想是通过连续层来补充通常的contracting网络,其中池化操作被上采样操作取代。因此,这些层提高了输出的分辨率。为了进行局部化,将来自收缩路径的高分辨率特征与上采样输出相结合。然后一个连续的卷积层可以学习根据这些信息组装一个更精确的输出。
我们架构中的一个重要修改是,在上采样部分,我们还有大量特征通道,这允许网络将上下文信息传播到更高分辨率的层。因此,扩展路径或多或少与收缩路径对称,并产生u形架构。网络没有任何全连接层,只使用每个卷积的有效部分,即分割图只包含输入图像中完整上下文可用的像素。该策略允许任意大的无缝分割重叠平铺策略的图像(参见图 2)。为了预测图像边界区域的像素,通过镜像输入图像来推断缺失的上下文。这种平铺策略对于将网络应用于大图像很重要,因为否则分辨率将受到GPU内存的限制。
至于我们的任务,可用的训练数据非常少,我们通过对可用的训练图像应用弹性变形来使用过多的数据增强。这允许网络学习对此类变形的不变性,而无需在带注释的图像语料库中查看这些转换。这在生物医学分割中尤为重要,因为变形曾经是组织中最常见的变化,并且可以有效地模拟真实的变形。 Dosovitskiy等人[2]在无监督特征学习的范围内显示了数据增强对学习不变性的价值。
许多细胞分割任务中的另一个挑战是同类接触物体的分离;参见图3。为此,我们建议使用加权损失,其中接触细胞之间的分离背景标签在损失函数中获得大的权重。
所得到的网络适用于各种生物医学分割问题。在本文中,我们展示了在EM堆栈中分割神经元结构的结果(这是一项始于ISBI 2012年的持续竞赛),在这方面,我们优于Ciresan等人的网络[1]。此外,我们展示了2015年ISBI细胞追踪挑战赛的光学显微镜图像中的细胞分割结果。在这里,我们在两个最具挑战性的2D透射光数据集上以较大优势获胜。
图 2. 任意大图像无缝分割的重叠平铺策略(这里是EM堆栈中神经元结构的分割)。黄色区域的分割预测,需要蓝色区域内的图像数据作为输入。通过镜像推断丢失的输入数据
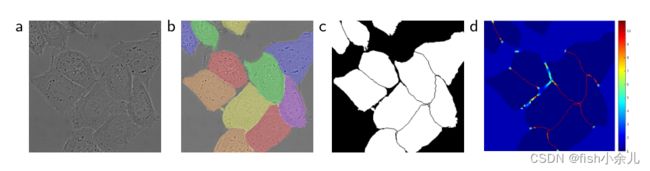
图 3. 用 DIC(微分干涉对比)显微镜记录的玻璃上的HeLa细胞。 (a) 原始图像。 (b) 与ground
truth分割叠加。不同的颜色表示HeLa细胞的不同实例。 (c ) 生成的分割掩码(白色:前景,黑色:背景)。 (d)使用逐像素损失权重进行映射,以强制网络学习边界像素
。
2 Network Architecture
网络架构如图1所示。它由收缩路径(左侧)和扩展路径(右侧)组成。收缩路径遵循卷积网络的典型架构。它由两个3x3卷积(未填充卷积)的重复应用组成,每个卷积后跟一个整流线性单元 (ReLU) 和一个2x2最大池化操作,步幅为2,用于下采样。在每个下采样步骤中,我们将特征通道的数量加倍。扩展路径中的每一步都包括对特征图进行上采样,然后是将特征通道数量减半的2x2卷积(“上卷积”),与收缩路径中相应裁剪的特征图的连接,以及两个3x3卷积,每个后跟一个ReLU。由于在每个卷积中都会丢失边界像素,因此裁剪是必要的。在最后一层,使用1x1卷积将每个64分量特征向量映射到所需数量的类。该网络总共有23个卷积层。
要实现输出分割图的无缝分块(见图2),选择输入分块大小很重要,这样所有2x2 max-pooling操作都可以应用到x和y大小相等的层。
3 Training
输入图像及其相应的分割图用于通过Caffe[6]的随机梯度下降实现来训练网络。由于无填充卷积,输出图像比输入图像小一个恒定的边界宽度。为了最大限度地减少开销并最大限度地利用GPU内存,我们倾向于使用较大的输入图块而不是较大的批处理大小,因此将批处理减少到单个图像。因此,我们使用高动量(0.99),使得大量先前看到的训练样本确定当前优化步骤中的更新。
能量函数是通过最终特征图上的像素级soft-max结合交叉熵损失函数来计算的。soft-max定义为 p k ( x ) = exp ( a k ( x ) ) / ( ∑ k ′ = 1 K exp ( a k ′ ( x ) ) ) p_{k}(\mathbf{x})=\exp \left(a_{k}(\mathbf{x})\right) /\left(\sum_{k^{\prime}=1}^{K} \exp \left(a_{k^{\prime}}(\mathbf{x})\right)\right) pk(x)=exp(ak(x))/(∑k′=1Kexp(ak′(x))),其中 a k ( x ) a_{k}(\mathbf{x}) ak(x)表示特征通道 k k k在像素位置 x ∈ Ω \mathbf{x} \in \Omega x∈Ω处的激活,其中 Ω ⊂ Z 2 \Omega \subset \mathbb{Z}^{2} Ω⊂Z2。 K K K是类数, p k ( x ) p_{k}(\mathbf{x}) pk(x)是近似的最大函数。即对于具有最大激活 a k ( x ) a_{k}(\mathbf{x}) ak(x)的 k k k, p k ( x ) ≈ 1 p_{k}(\mathbf{x}) \approx 1 pk(x)≈1,对于所有其他 k k k, p k ( x ) ≈ 0 p_{k}(\mathbf{x}) \approx 0 pk(x)≈0。然后交叉熵在每个位置惩罚 p ℓ ( x ) ( x ) p_{\ell(\mathbf{x})}(\mathbf{x}) pℓ(x)(x)与1的偏差,使用
E = ∑ x ∈ Ω w ( x ) log ( p ℓ ( x ) ( x ) ) (1) E=\sum_{\mathbf{x} \in \Omega} w(\mathbf{x}) \log \left(p_{\ell(\mathbf{x})}(\mathbf{x})\right) \tag{1} E=x∈Ω∑w(x)log(pℓ(x)(x))(1)
其中 ℓ : Ω → { 1 , … , K } \ell: \Omega \rightarrow\{1, \ldots, K\} ℓ:Ω→{1,…,K}是每个像素的真实标签, w : Ω → R w: \Omega \rightarrow \mathbb{R} w:Ω→R是我们引入的权重图,以便在训练中赋予一些像素更多的重要性。
我们预先计算每个ground truth分割的权重图,以补偿训练数据集中某个类别的像素的不同频率,并强制网络学习我们在接触单元之间引入的小分离边界(见图3c和d)。
使用形态学运算计算分离边界。然后将权重图计算为
w ( x ) = w c ( x ) + w 0 ⋅ exp ( − ( d 1 ( x ) + d 2 ( x ) ) 2 2 σ 2 ) (2) w(\mathbf{x})=w_{c}(\mathbf{x})+w_{0} \cdot \exp \left(-\frac{\left(d_{1}(\mathbf{x})+d_{2}(\mathbf{x})\right)^{2}}{2 \sigma^{2}}\right) \tag{2} w(x)=wc(x)+w0⋅exp(−2σ2(d1(x)+d2(x))2)(2)
其中 w c : Ω → R w_{c}: \Omega \rightarrow \mathbb{R} wc:Ω→R是平衡类频率的权重图, d 1 : Ω → R d_{1}: \Omega \rightarrow \mathbb{R} d1:Ω→R表示到最近单元格边界的距离, d 2 : Ω → R d_{2}: \Omega \rightarrow \mathbb{R} d2:Ω→R表示到第二最近单元格边界的距离。在我们的实验中,我们设置 w 0 = 10 w_{0}=10 w0=10和 σ ≈ 5 \sigma \approx 5 σ≈5个像素。
在具有许多卷积层和通过网络的不同路径的深度网络中,良好的权重初始化非常重要。否则,网络的某些部分可能会提供过多的激活,而其他部分则永远不会做出贡献。理想情况下,应该调整初始权重,使得网络中的每个特征图都具有近似单位方差。对于具有我们架构的网络(交替卷积和ReLU层),这可以通过从标准差为 2 / N \sqrt{2 / N} 2/N的高斯分布中提取初始权重来实现,其中 N N N表示一个神经元的传入节点数[5]。例如,对于前一层中的3x3卷积和64个特征通道, N = 9 ⋅ 64 = 576 N=9 \cdot 64=576 N=9⋅64=576。
3.1 Data Augmentation
当只有很少的训练样本可用时,数据增强对于教会网络所需的不变性和鲁棒性是必不可少的。在显微图像的情况下,我们主要需要移位和旋转不变性以及对变形和灰度值变化的鲁棒性。特别是训练样本的随机弹性变形似乎是训练带有很少注释图像的分割网络的关键概念。我们使用粗略的3 x 3网格上的随机位移矢量生成平滑变形。位移是从具有 10 像素标准偏差的高斯分布中采样的。然后使用双三次插值计算每像素位移。收缩路径末端的 drop-out 层执行进一步的隐式数据增强。
5 Conclusion
u-net架构在非常不同的生物医学分割应用程序上实现了非常好的性能。由于具有弹性变形的数据增强,它只需要很少的注释图像,并且在 NVidia Titan GPU (6 GB)上的训练时间非常合理,只有10小时。我们提供完整的基于Caffe[6]的实现和训练有素的网络。我们确信u-net架构可以轻松应用于更多任务。
原文链接:https://arxiv.org/pdf/1505.04597.pdf