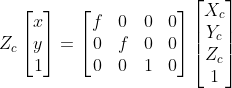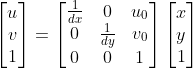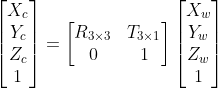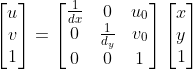标定学习笔记（一）-- 单目相机的标定
一文图解单目相机标定算法 (qq.com)
一、什么是相机标定？
任何传感器都存在一定的误差，从狭义上来说，标定就是去校正这部分的误差，让传感器尽量准确一点。
相机要进行标定的参数，跟相机实际的光圈、焦距大小有关，而这两个参数，在一般的工业相机中都是可调节的，所以需要我们针对实际情况进行标定。
常说的标定不光指纠正传感器的误差，当涉及到两个或者多个传感器的标定的时候，往往还包括计算出这些传感器间的相互位置关系。比如说在机器人系统中，我们经常需要在不同坐标系下转换位置关系，那么我们所说的一些标定还包括标定出这些关节、传感器之间的相互位置关系。再比如说我们双目相机的标定，就包括左相机、右相机的传感器误差标定，还包括它们之间相互位置关系的这么一个标定。
概括一下，常说的标定包括两部分的内容：传感器误差的校正、传感器相互之间的位置关系。而单目相机的标定主要是指前者：传感器误差的校正，常用的方法是张正友标定法。
常见的单目相机标定方法是张正友标定法，这在很多软件，比如MATLAB、或者OpenCV中都有相应的实现。至于相机标定，需要标定哪些参数，还需要先来了解下单目相机的成像模型。
二、理想单目相机成像模型
在介绍高斯光学时，我们介绍了小孔成像与针孔相机模型的基础。实际上，小孔成像的模型其实可以看作是针孔相机模型的基础：
进一步地，针孔相机模型可以简化为下面这个模型：
上图中，P点是物点，p'是前者在CCD上成像的像点，
是相机的光心，
是成像平面到光心的距离，我们称之为焦距。
实际上，焦距的定义会更复杂，可以参考我们之前在机器视觉学习笔记相机中的描述。
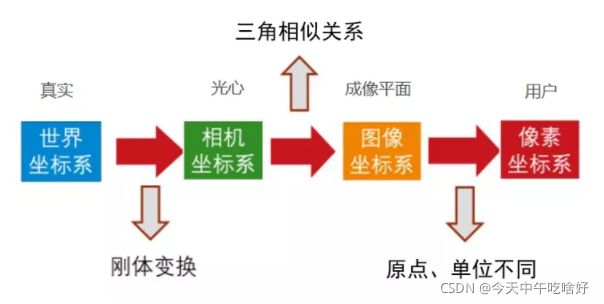
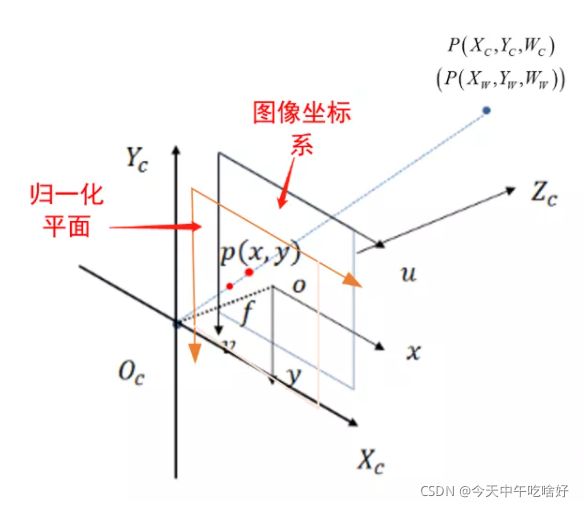
这里先把模型简化一下，下面我们来讲解整个成像过程，在相机成像模型中，主要有四大坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系。
其中：
1）世界坐标系
（3D）：世界坐标系就是以外界某个参考点建立的坐标系，单位为mm，或者m。
2）相机坐标系
（3D）：以光心建立相机坐标系，其中轴指向相机的正前方。
3）图像坐标系
（2D）：光心在成像平面的投影，光心为图像中点o点，以o点建立另一坐标系，称为图像坐标系，单位为mm。
4）像素坐标系
（2D）：像素坐标系是我们最终用户所看到的，也就是坐标系的原点在图像左上角，单位为像素。
为了建立实际物理点（世界坐标系）到图像上点（像素坐标系）的一一映射，我们需要三步转换，也就是：
世界坐标系 
相机坐标系 图像坐标系 像素坐标系
2.1 世界坐标系 相机坐标系
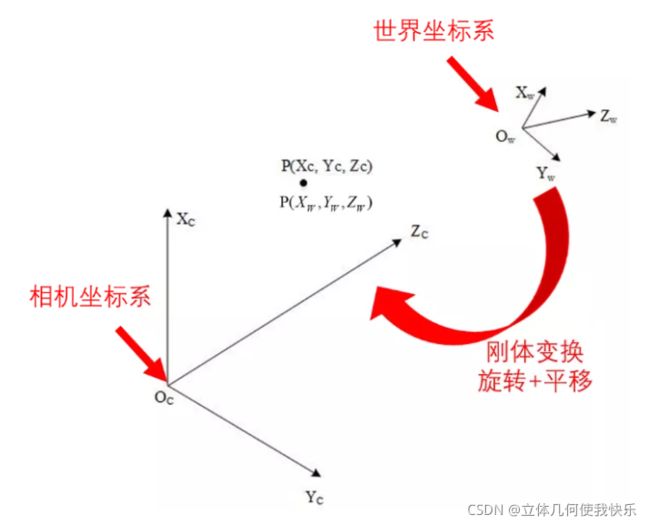
首先，我们知道，世界坐标系是以外界某个参考点建立的坐标系，而相机坐标系则是以相机的光心为坐标原点，光轴的正方向作为Z轴建立的坐标系，两者属于刚体变换，只需要进行旋转和平移，如下所示：
我们假设物点在世界坐标系下的坐标为
，那么转换到相机坐标系下坐标
的变换如下：
(为了统一旋转和平移，我们将其写为齐次形式)
2.2 相机坐标系 图像坐标系
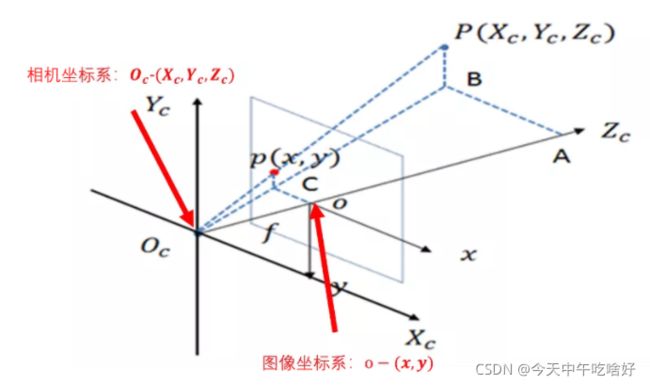
在完成了世界坐标系 相机坐标系的转换后，我们再从相机坐标系转换到图像坐标系。为了方便描述，我们将针孔相机模型对称翻转过来，如下图所示，从数学的角度，它们是等价的：
如我们之前所说的，P点是物点、P'点是像点，现在我们将它反转过来了，记作小写的p，其中：
相机坐标系：以光心建立相机坐标系
，其中
轴指向相机的正前方。
图像坐标系：光心在成像平面的投影，也就是
点建立另一坐标系，称为图像坐标系。
物点P在相机坐标系下的坐标，记为
，而像点p可以记为
，根据简单的相似三角形的关系，很容易可以得到：
与之前俺的公式进行统一，写为齐次形式：
2.3 图像坐标系 像素坐标系
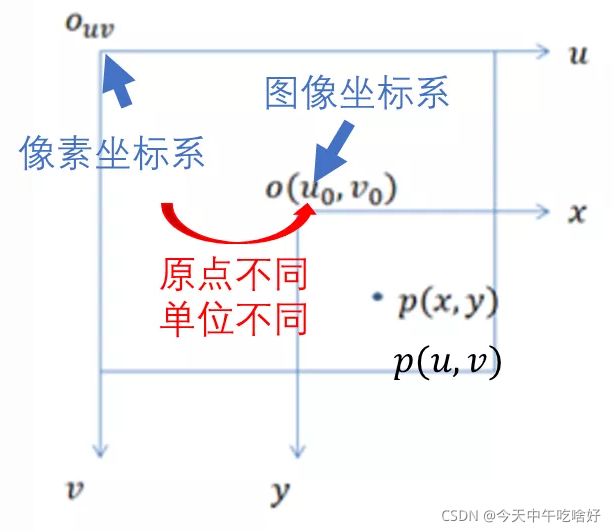
在图像坐标系中，坐标的原点在图像中间，而我们平时处理图像时用的坐标系，称为像素坐标系，坐标系的原点在图像的左上角，此外它们的度量单位也不同，前者的单位是mm，而后者的单位是像素。
总结一下，图像坐标系和像素坐标系主要有两点不同：原点不同、单位不同。
我们用
来记录像素的列数与行数，那么：
1）图像坐标系下坐标系原点，在像素坐标系
下记为：
；
2）像点p，在坐标系下记为：
；
此外，再分别记dx、dy为每个像素在x轴、y轴所代表的物理尺寸，我们很容易可以从上图中推导出下列关系：
将其进行移项，并写为齐次的形式，有：
2.4 汇总
总结一下之前所说的四大坐标系的关系：
它们的公式如下：
1）世界坐标系 相机坐标系
（刚体变换）
2）相机坐标系 图像坐标系
（相似三角形）
3）图像坐标系 像素坐标系
将上述的式子进行联立，最终可以得到：
进一步化简：
这个公式就是整个单目相机在理想情况下的成像公式，可以建立世界坐标系到像素坐标系的一一映射。
补充一点：
归一化平面，其实际是图像坐标系的等比缩放，也就是当焦距
的情况，主要是便于公式的推导，它与图像坐标系是等比缩放关系，只需要乘以焦距就可完成相互转换。
