自学神经网络系列—— 10 循环神经网络 RNN
循环神经网络
- 1 简单循环神经网络
- 2 循环神经网络的常见应用
-
- 2.1 序列标注任务
- 2.2 分类预测任务
- 2.3 机器翻译
- 3 循环神经网络的参数学习
-
- 3.1 实时循环学习RTRL
- 3.2 随时间反向传播 BPTT
- 3.3 梯度爆炸和梯度消失
- 4 其他循环神经网络
-
- 4.1 深度循环神经网络
- 4.1双向循环神经网络
- 循环神经网络是一种动态建模方法,常用于序列分析,比如本文序列建模、时间序列预测等等。本篇文章主要参考了邱锡鹏老师的《神经网络与深度学习》。
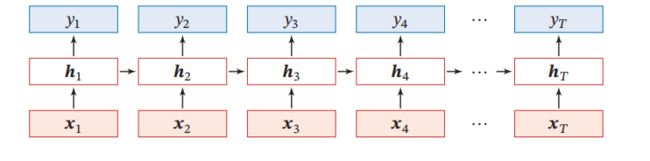
- 循环神经网络可以看作前馈神经网络(全连接神经网络和卷积神经网络)在时序上的展开,即对序列 { X t } \{X_t\} {Xt}在每个时点上的随机变量 x t x_t xt建立前馈神经网络。循环神经网络不仅可以接受输入变量 x t + 1 x_{t+1} xt+1而且能够将上一时点前馈神经网络的隐藏状态传递到下时点上的前馈神经网络中,类似于时间序列分析中的ARDL模型 h t = f ( h t − 1 , h t − 2 , . . . , h t − m , x t , x t − 1 , x t − 2 , . . . , x t − n ) h_t = f(h_{t-1},h_{t-2},...,h_{t-m},x_{t},x_{t-1},x_{t-2},...,x_{t-n}) ht=f(ht−1,ht−2,...,ht−m,xt,xt−1,xt−2,...,xt−n)。循环神经网络具体结构如下:
1 简单循环神经网络
- 最简单的循环神经网络每个时点使用只有一个隐藏层的前馈神经网络,然后将不同时点的前馈神经网络连接起来,结构如下:
-
当 t = 1 t=1 t=1时,训练一个单隐藏层的前馈神经网络
-
当 t > 1 t>1 t>1时,相当于每一个隐藏层将上一时刻隐藏层大小的向量 h t − 1 h_{t-1} ht−1和输入 x t {x_t} xt拼接起来输入隐藏层进行训练,并且将各个时刻的隐藏状态序列 h t {h_t} ht、输出序列 { y t } \{y_t\} {yt}保存下来。
h t = R e l u ( U h t − 1 + W x t + b ) y t = V h t h_t = Relu(Uh_{t-1}+Wx_t+b) \\ y_t = Vh_t ht=Relu(Uht−1+Wxt+b)yt=Vht -
从公式可以看出循环神经网络的参数是共享权重的
2 循环神经网络的常见应用
2.1 序列标注任务
循环神经网络非常适合序列标注任务,比如比较常见的词性标注任务需要为每一个词生成词性标签,所以可以使用训练循环神经网络时,保存的输出序列 { y t } \{y_t\} {yt}预测当前时刻输入词的词性。
2.2 分类预测任务
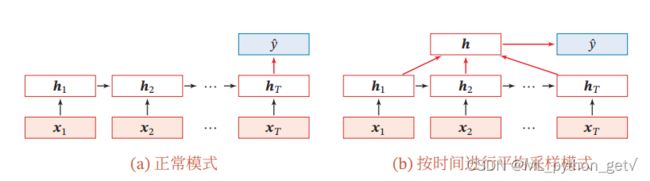
在时间序列分析中,我们比较关心的是下一个时刻发生的事情,所以需要对某一时刻的变量进行预测。通常情况下,我们通常选用下一个时刻的值输出 y t + 1 y_{t+1} yt+1进行预测。但是在某些情况下,我们需要对整个序列的属性进行分析,比如在情感分析中通常使用平均采样法对句子属性进行预测。
- 最后时刻法: 将最后时刻的状态 h T h_T hT作为整个序列的表示
- 平均采样法:将保存的 { h t } \{h_t\} {ht}在时间上取平均得到整个序列的表示
- 最后将序列表示输入sigmoid或者softmax函数进行分类
2.3 机器翻译
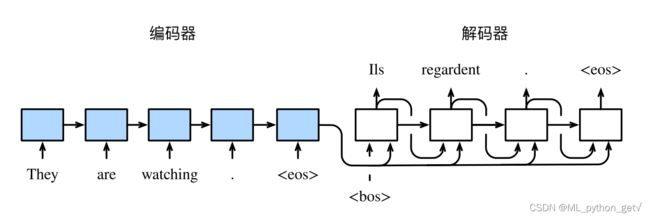
在机器翻译任务中,不同语言翻译内容长度有很大差异,输入序列和输出序列通常不等长,使用传统的RNN进行建模,不像分类和标注任务那么容易选择合适的输出序列。机器翻译领域较为著名的Seq2Seq模型在编码器-解码器架构下使用了两个RNN进行建模。
- 编码器负责将输入序列 { x t } \{x_t\} {xt}转化为隐藏状态序列 { h t } \{h_t\} {ht}
- embeding向量通常取最后时刻的隐藏状态 h T h_T hT
- 解码器负责将embdedding向量 h T h_T hT转化为隐藏状态序列 { h T + t } \{h_{T+t}\} {hT+t}
- 编码器输入被翻译的序列 { x t } \{x_t\} {xt},输出隐藏状态序列 { h t } \{h_t\} {ht}
- 训练时:解码器输入embeding向量 h T h_T hT和真实翻译序列 { s T + t } \{s_{T+t}\} {sT+t}
- 预测时:解码器输入embeding向量 h T h_T hT和解码器上一时刻隐藏状态 { h T + t } \{h_{T+t}\} {hT+t}进行预测
- 解码器输出隐藏状态序列 { h T + t } \{h_{T+t}\} {hT+t}作为翻译结果
3 循环神经网络的参数学习
不同于前馈神经网络,循环神经网络在每一时刻都有一个预测值和一个标签,那么就可以在每一时刻计算损失进行梯度下降,基于这种思想循环神经网络可以使用两种学习算法进行参数更新。公式推导可参考邱锡鹏老师的《神经网络与深度学习》。
- 循环神经网络:共享权重
- 实时循环学习 RTRL:针对每一时刻的损失函数进行学习,
- 随时间反向传播 BPTT:针对所有时刻的损失函数进行学习,类似于普通反向传播,根据t+1和t时刻的迭代公式,反求梯度。
3.1 实时循环学习RTRL
- t时刻前向传播
h t = R e l u ( U h t − 1 + W x t + b ) y t = V h t h_t = Relu(Uh_{t-1}+Wx_t+b) \\ y_t = Vh_t ht=Relu(Uht−1+Wxt+b)yt=Vht - t时刻损失函数
L t = ( y t , y ^ t ) L_t = (y_t,\hat y_t) Lt=(yt,y^t) - t时刻梯度
- 实时循环算法认为 h t − 1 、 h t h_{t-1}、h_t ht−1、ht都是U、W、b的函数
∂ L t ∂ u i j = ∂ L t ∂ h t ∂ h t ∂ u i j {\partial L_t \over \partial u_{ij}} = {\partial L_t \over \partial h_t}{\partial h_t \over \partial u_{ij}} ∂uij∂Lt=∂ht∂Lt∂uij∂ht - 令 Z t = U h t − 1 + W x t + b 令Z_t = Uh_{t-1}+Wx_t+b 令Zt=Uht−1+Wxt+b
∂ h t ∂ u i j = ∂ h t ∂ Z t ∂ Z t ∂ u i j = ∂ h t ∂ Z t ( ∂ U ∂ u i j h t − 1 + ∂ h t − 1 ∂ u i j U ′ ) {\partial h_t \over \partial u_{ij}} = {\partial h_t \over \partial Z_{t}}{\partial Z_t \over \partial u_{ij}} ={\partial h_t \over \partial Z_{t}} ({\partial U \over \partial u_{ij}}h_{t-1}+ {\partial h_{t-1} \over \partial u_{ij}}U') ∂uij∂ht=∂Zt∂ht∂uij∂Zt=∂Zt∂ht(∂uij∂Uht−1+∂uij∂ht−1U′)
∂ h t ∂ w i j = ∂ h t ∂ Z t ∂ Z t ∂ w i j = ∂ h t ∂ Z t ( ∂ h t − 1 ∂ w i j U ′ + x t ) {\partial h_t \over \partial w_{ij}} = {\partial h_t \over \partial Z_{t}}{\partial Z_t \over \partial w_{ij}} ={\partial h_t \over \partial Z_{t}} ( {\partial h_{t-1} \over \partial w_{ij}}U'+x_t) ∂wij∂ht=∂Zt∂ht∂wij∂Zt=∂Zt∂ht(∂wij∂ht−1U′+xt)
∂ h t ∂ b i = ∂ h t ∂ Z t ∂ Z t ∂ b i = ∂ h t ∂ Z t ( ∂ h t − 1 ∂ b i U ′ + 1 ) {\partial h_t \over \partial b_{i}} = {\partial h_t \over \partial Z_{t}}{\partial Z_t \over \partial b_{i}} ={\partial h_t \over \partial Z_{t}} ( {\partial h_{t-1} \over \partial b_{i}}U'+1) ∂bi∂ht=∂Zt∂ht∂bi∂Zt=∂Zt∂ht(∂bi∂ht−1U′+1)- 前向计算的递推公式 ∂ h t − 1 ∂ u i j {\partial h_{t-1} \over \partial u_{ij}} ∂uij∂ht−1推导 ∂ h t ∂ u i j {\partial h_t \over \partial u_{ij}} ∂uij∂ht
- ∂ h t ∂ Z t {\partial h_t \over \partial Z_{t}} ∂Zt∂ht 为激活函数的导数,实时计算
- ∂ U ∂ u i j h t − 1 {\partial U \over \partial u_{ij}}h_{t-1} ∂uij∂Uht−1 需要保存上一层隐藏状态
- ∂ h t − 1 ∂ u i j {\partial h_{t-1} \over \partial u_{ij}} ∂uij∂ht−1 需要保存上一层隐藏状态对系数的梯度
- 实时循环算法认为 h t − 1 、 h t h_{t-1}、h_t ht−1、ht都是U、W、b的函数
3.2 随时间反向传播 BPTT
考虑到所有时刻累积的损失,类似普通的反向传播算法,考察某一时刻k的系数对T时刻损失的影响。

- 与实时循环算法不同的是:BPTT算法在计算梯度时认为k-1时刻的隐藏状态 h t − 1 h_{t-1} ht−1不再随U发生变化,所以梯度公式为
∂ L t ∂ u i j = ∑ k = 1 t ∂ L t ∂ z k ∂ z k ∂ u i j = ∑ k = 1 t ∂ L t ∂ z k h k − 1 j {\partial L_t \over \partial u_{ij}} = \sum_{k=1}^t {\partial L_t \over \partial z_{k}} {\partial z_k \over \partial u_{ij}} = \sum_{k=1}^t {\partial L_t \over \partial z_{k}} h_{k-1_j} ∂uij∂Lt=k=1∑t∂zk∂Lt∂uij∂zk=k=1∑t∂zk∂Lthk−1j - 任意时刻t的反向传播算法
δ t ( k ) = ∂ L t ∂ z k = ∂ L t ∂ z k + 1 ∂ z k + 1 ∂ h k ∂ h k ∂ z k = δ t ( k + 1 ) U ′ ∂ h k ∂ z k \delta_t(k) = {\partial L_t \over \partial z_{k}} = {\partial L_t \over \partial z_{k+1}} {\partial z_{k+1} \over \partial h_{k}}{\partial h_k \over \partial z_{k}} = \delta_t(k+1)U'{\partial h_k \over \partial z_{k}} δt(k)=∂zk∂Lt=∂zk+1∂Lt∂hk∂zk+1∂zk∂hk=δt(k+1)U′∂zk∂hk- 类似普通反向传播算法,误差可以在时刻k+1传导到时刻k上
- 并没有对 h k − 1 h_{k-1} hk−1 进行求导
- 递推公式是反向传播形式
- 将所有时刻的梯度累加即可得到最终损失函数对参数的梯度
∂ L T ∂ u = ∑ t = 1 T ∑ k = 1 t ∂ L t ∂ z k ∂ z k ∂ u i j = ∑ t = 1 T ∑ k = 1 t ∂ L t ∂ z k h k − 1 {\partial L_T\over \partial u} = \sum _{t=1}^T \sum_{k=1}^t {\partial L_t \over \partial z_{k}} {\partial z_k \over \partial u_{ij}} = \sum _{t=1}^T \sum_{k=1}^t {\partial L_t \over \partial z_{k}} h_{k-1} ∂u∂LT=t=1∑Tk=1∑t∂zk∂Lt∂uij∂zk=t=1∑Tk=1∑t∂zk∂Lthk−1
∂ L T ∂ w = ∑ t = 1 T ∑ k = 1 t ∂ L t ∂ z k ∂ z k ∂ w = ∑ t = 1 T ∑ k = 1 t ∂ L t ∂ z k x k ′ {\partial L_T\over \partial w} = \sum _{t=1}^T \sum_{k=1}^t {\partial L_t \over \partial z_{k}} {\partial z_k \over \partial w} = \sum _{t=1}^T \sum_{k=1}^t {\partial L_t \over \partial z_{k}} x_k' ∂w∂LT=t=1∑Tk=1∑t∂zk∂Lt∂w∂zk=t=1∑Tk=1∑t∂zk∂Ltxk′
∂ L T ∂ b = ∑ t = 1 T ∑ k = 1 t ∂ L t ∂ z k ∂ z k ∂ b = ∑ t = 1 T ∑ k = 1 t ∂ L t ∂ z k {\partial L_T\over \partial b} = \sum _{t=1}^T \sum_{k=1}^t {\partial L_t \over \partial z_{k}} {\partial z_k \over \partial b} = \sum _{t=1}^T \sum_{k=1}^t {\partial L_t \over \partial z_{k}} ∂b∂LT=t=1∑Tk=1∑t∂zk∂Lt∂b∂zk=t=1∑Tk=1∑t∂zk∂Lt- 两者都是基于梯度下降的算法
- RTRL是前向算法,BPTT是后向算法
- RTRL在时刻t上进行梯度下降,需要考虑到前一层隐藏状态的优化,所以是一种“实时”和“循环”的算法,即计算认为隐藏状态 h t − 1 h_{t-1} ht−1随U发生变化,需要对 h t − 1 h_{t-1} ht−1计算梯度。
- BPTT在整个序列上进行梯度下降,不需要考虑到前一层隐藏状态的局部优化,类似于普通的反向传播算法,计算认为隐藏状态 h t − 1 h_{t-1} ht−1已经固定,不需要对 h t − 1 h_{t-1} ht−1计算梯度。
- RTRL需要保存所有时刻的中间梯度,但是可以实时计算梯度,牺牲了空间复杂度,适合在线计算。
- BPTT需要反传后面时刻的误差,牺牲了时间复杂度。但是在输出维度较小的情况下,又提高了计算效率,适合大规模训练。
3.3 梯度爆炸和梯度消失
-
对于任意时刻k的反向传播算法
δ t ( k ) = ∂ L t ∂ z k = ∂ L t ∂ z k + 1 ∂ z k + 1 ∂ h k ∂ h k ∂ z k = δ t ( k + 1 ) U ′ ∂ h k ∂ z k \delta_t(k) = {\partial L_t \over \partial z_{k}} = {\partial L_t \over \partial z_{k+1}} {\partial z_{k+1} \over \partial h_{k}}{\partial h_k \over \partial z_{k}} = \delta_t(k+1)U'{\partial h_k \over \partial z_{k}} δt(k)=∂zk∂Lt=∂zk+1∂Lt∂hk∂zk+1∂zk∂hk=δt(k+1)U′∂zk∂hk
不同于传统的反向传播算法,RNN中的反向传播是依赖于时间间隔t-k的,即 δ t ( k ) = ( U ′ ∂ h k ∂ z k ) t − k δ t ( t ) \delta_t(k) = (U'{\partial h_k \over \partial z_{k}})^{t-k}\delta_t(t) δt(k)=(U′∂zk∂hk)t−kδt(t) -
梯度爆炸:当 ( U ′ ∂ h k ∂ z k ) (U'{\partial h_k \over \partial z_{k}}) (U′∂zk∂hk)>1时会产生梯度爆炸问题:激活函数虽然小于1但是参数U可能很大
- 参数更新幅度变得很大,难以达到最优点
- 可能会超出计算机允许的范围
-
梯度消失:当 ( U ′ ∂ h k ∂ z k ) (U'{\partial h_k \over \partial z_{k}}) (U′∂zk∂hk)<1时会产生梯度消失问题:激活函数小于1,起主导作用。
- 梯度消失的是 ∂ L t ∂ z k {\partial L_t \over \partial z_{k}} ∂zk∂Lt部分;梯度 ∂ L t ∂ U {\partial L_t \over \partial U} ∂U∂Lt是要通过时间累加的,一般不会消失
- 参数停止更新,训练效率低
-
长序列建模问题: ∂ L t ∂ z k {\partial L_t \over \partial z_{k}} ∂zk∂Lt会趋于0,导致距离时间长的冲击对时刻t影响几乎为0,导致RNN难以对长序列进行建模。
-
改进方法
- 梯度爆炸:比较容易解决,正则化参数、梯度截断
- 梯度消失:循环神经网络的主要问题,引入线性项 h t = h t − 1 + g ( h t − 1 , x ) h_t = h_{t-1}+g(h_{t-1},x) ht=ht−1+g(ht−1,x)
- 引入线性项同样会引发梯度爆炸问题:在原来的梯度上+1
- 一直累加 h t − 1 h_{t-1} ht−1 会使得激活函数达到饱和,仍然不能对长序列进行建模
4 其他循环神经网络
4.1 深度循环神经网络
为了获得更多的非线性性,每一个时刻不再是单隐藏层的前馈神经网络,而是多隐藏层的前馈神经网络,其结构如图所示:
- 略微修改循环神经网络模型即可
- 简单循环神经网络
h t = R e l u ( U h t − 1 + W x t + b ) y t = V h t h_t = Relu(Uh_{t-1}+Wx_t+b) \\ y_t = Vh_t ht=Relu(Uht−1+Wxt+b)yt=Vht - 深度循环神经网络
h t 1 = R e l u ( U 1 h t − 1 1 + W 1 x t + b 1 ) h t 2 = R e l u ( U 2 h t − 1 2 + W 2 h t 1 + b 2 ) . . . h t j = R e l u ( U j h t − 1 j + W j h t j − 1 + b j ) . . . y t = V h t L h_t^1 = Relu(U^1h_{t-1}^1+W^1x_t+b^1) \\ h_t^2 = Relu(U^2h_{t-1}^2+W^2h_{t}^1+b^2)\\...\\h_t^j = Relu(U^jh_{t-1}^j+W^jh_{t}^{j-1}+b^j) \\...\\ y_t = Vh_t^L ht1=Relu(U1ht−11+W1xt+b1)ht2=Relu(U2ht−12+W2ht1+b2)...htj=Relu(Ujht−1j+Wjhtj−1+bj)...yt=VhtL
4.1双向循环神经网络
为了获得整个时序信息,每一个时刻不再是只获得过去信息,而是建立两个RNN,一个正向RNN,一个反向RNN,反向RNN将序列翻转即可实现,反向RNN隐藏状态反向后,将两个隐藏状态concat在一起通过最后一层分类器即可。其结构如图所示:
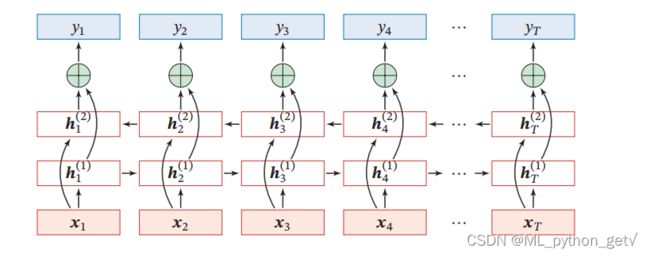
- 双向循环神经网络
h t f = R e l u ( U f h t − 1 f + W f x t f + b f ) h t b = R e l u ( U b h t + 1 b + W b x t b + b b ) h t = c o n c a t ( h t f , h t b ) y t = V h t h_t^f = Relu(U^fh_{t-1}^f+W^fx_t^f+b^f) \\ h_t^b = Relu(U^bh_{t+1}^b+W^bx_{t}^b+b^b)\\ h_t = concat(h_t^f,h_t^b)\\ y_t = Vh_t htf=Relu(Ufht−1f+Wfxtf+bf)htb=Relu(Ubht+1b+Wbxtb+bb)ht=concat(htf,htb)yt=Vht - 预测时无未来信息
- 一般用来抽取句子信息
- 不能用来预测