【人工智能与机器学习】——朴素贝叶斯与支持向量机（学习笔记）

前言：朴素贝叶斯（Naive Bayes）和支持向量机（Support Vector Machine，SVM）是两种不同的机器学习算法，它们都用于分类。朴素贝叶斯算法基于贝叶斯定理来进行分类，它是一种生成模型，它预测一个样本属于某个类别的概率。相比之下，支持向量机是一种判别模型，它用于寻找数据空间的最大边界来进行分类。

---

1. 概率知识回顾

贝叶斯公式：
$$P(C\mid X)=\frac{P(X\mid C)\ast P(C)}{P(X)}$$

下面来了解各个成分的含义：

• P（C | X），是给定某个对象X，它属于类别C的后验概率。
• P（C），是类别C的先验概率。
• P（X | C），是给定类别C的条件下，它是对象X的条件概率。
• P（X），是对象X的先验概率。

例如，在新冠病毒诊断中，X表示各个症状的情况，C表示诊断的结果，它有两个值，分别是有病和没病。P(C | X）就表示给定当前症状情况的诊断结果，有病和没病的概率分别是多少，对其预测是一件非常困难的事情，于是可以利用一些先验概率来计算和比较。P(X)表示症状发生的先验概率。P©表示有病或没病的先验概率，比如1000个人里面，100个人有病，900个人没病，那么P(C=有病)=0.1，P(C=没病)=0.9。P(X | C)表示在有病或者没病的情况下，具有症状情况X的概率是多少。此外，根据症状程度，我们也可以划分为轻微、中度、严重

$\begin{array}{ccccccc}\text{ 发热 }& \text{ 干咳 }& \text{ 乏力 }& \text{ 鼻塞流涕 }& \text{ 咽痛 }& \text{ 腹泻 }& \text{ 诊断 }\\ \text{ 轻微 }& \text{ 严重 }& \text{ 轻微 }& \text{ 中度 }& \text{ 无 }& \text{ 无 }& \text{ 否 }\\ \text{ 中度 }& \text{ 轻微 }& \text{ 中度 }& \text{ 中度 }& \text{ 轻微 }& \text{ 无 }& \text{ 是 }\\ \text{ 无 }& \text{ 轻微 }& \text{ 无 }& \text{ 轻微 }& \text{ 无 }& \text{ 无 }& \text{ 否 }\\ \text{ 严重 }& \text{ 无 }& \text{ 严重 }& \text{ 中度 }& \text{ 轻微 }& \text{ 无 }& \text{ 是 }\\ \text{ 轻微 }& \text{ 无 }& \text{ 中度 }& \text{ 无 }& \text{ 中度 }& \text{ 轻微 }& \text{ 否 }\end{array}$

我们可以把每个症状都单独计算一遍，但实际并不需要这么做
$$P(X)=\sum _{Z}P(X,Z)=\sum _{Z}P(X\mid Z)\ast P(Z)$$
$$P(C\mid X)=\frac{P(X\mid C)\ast P(C)}{P(X)}$$
$$\text{ posterior }=\frac{\text{ likelihood }\ast \text{ prior }}{\text{ evidence }}$$

2. 训练贝叶斯

给定特征向量()，计算其属于每个类别（C）的概率
$P(C\mid X)=P(X\mid C)\ast P(C)$
很难计算所有特征的联合概率
$$\begin{gathered} P(C\mid X)=P\left(X_1,X_2,\dots ,X_n\mid C\right)\ast P(C) \\ =P\left(X_1\mid X_2,\dots ,X_n,C\right)\ast P\left(X_2,\dots ,X_n\mid C\right)\ast P(C) \end{gathered}$$
解决方案：假设给定类别，所有特征相互独立
$P(C\mid X)=P\left(X_1\mid C\right)\ast P\left(X_2\mid C\right)\ast P\left(X_n\mid C\right)\ast P(C)$
这就是“朴素”的假设
$P(C\mid X)=P(C){\prod }_{i=1}^{n}P\left(X_i\mid C\right)$
按照最大后验概率规则，把X分入概率最大的类别
$\frac{\mathrm{argmax}}{k\in \{1,\dots K\}}P\left(C_k\right){\prod }_{i=1}^{n}P\left(X_i\mid C_k\right)$
很多概率值连乘，容易造成浮点计算下界溢出
取对数把乘法转化成加法
$\log \left(P\left(C_k\right)\right){\sum }_{i=1}^n\log \left(P\left(X_i\mid C_k\right)\right)$

3. 朴素贝叶斯分类器

接下来，我们用预测打网球这个案例展开讲解

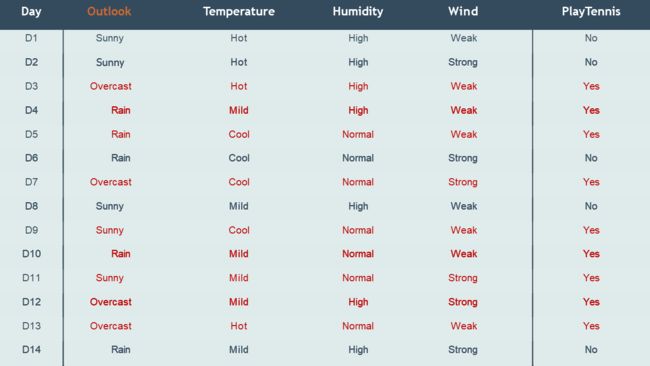
使用训练数据构建概率查找表

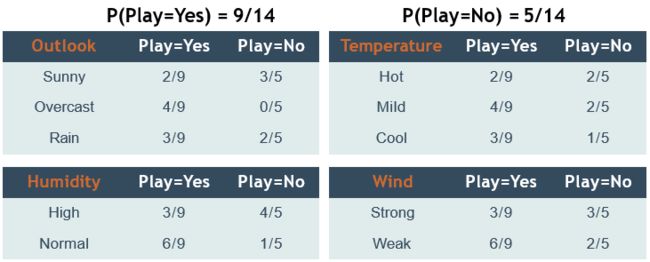
预测下面情境下是否打网球：
x’=(Outlook=Sunny, Temperature=Cool, Humidity=High, Wind=Strong)

$$\begin{gathered} P(\text{ yes | sunny, cool, high, strong })=P(\text{ sunny | yes })\times P(\text{ cool | yes })\times P(\text{ high | yes })\times P(\text{ strong | yes })\times P(\text{ yes }) \\ P(\text{ no | sunny, cool, high, strong })=P(\text{ sunny | no })\times P(\text{ cool | no })\times (\text{ high | no })\times P(\text{ strong | no })\times P(\text{ no }) \end{gathered}$$

结果是否

3.1 优缺点

优点：
（1）原理简单，容易实现。
（2）很容易进行模型训练,适合各种规模的数据集。
（3）运行速度快，除二分类问题之外，它在多分类问题上也表现良好。由于运行速度快，可以利用朴素贝叶斯分类器进行实时预测，这在需要实时处理的场景中是非常有用的。
（4）如果各变量之间确实是相互独立的，那么朴素贝叶斯分类器和其他分类器如逻辑回归模型相比，有时候分类的准确性更好，而且需要更少的训练数据。
（5）即便模型包含无关的输人变量，模型的表现（分类准确性）也很好。

缺点：
（1）它假设变量之间是相互独立的，而这在实际中往往不成立。
（2）如果某个类别变量的取值在测试数据集中出现，但是在训练集中没有出现过（比如身高值是个线性值），那么分类器给一个为0的概率，导致整个计算结果是0，就无法进行正确预测了。零概率问题可以通过平滑技术来处理，拉普拉斯平滑技术是常见的一种方法。
（3）对于数值型变量，一般假设是正态分布，这是一个较强的假设，有时候实际情况并非如此。

3.2 拉普拉斯平滑技术

零概率问题：在计算事件的概率时，如果某个事件在观察样本库（训练集）中没有出现过，会导致该事件的概率结果是0。这是不合理的，不能因为一个事件没有观察到，就被认为该事件一定不可能发生（即该事件的概率为0）。

拉普拉斯平滑（Laplacian smoothing）就是为了解决零概率的问题而产生。方法是在这些条件概率的分子和分母上各加$\alpha$和$\alpha \ast Count(X_i)$（α-拉普拉斯平滑系数，常取1，Count(X_i)为特征X_i的不同取值数，比如X₁有3个选项，那么Count(X₁)为3，$n_c$即类别数目）

$$P(C\mid X)=P\left(X_1\mid C\right)\ast P\left(X_2\mid C\right)\ast P(C)$$
假设$P(X_1\mid C)$的值为0，那么公式应该如下：
$P\left(X_1\mid C\right)=\frac{0+1}{\mathrm{Count}(X_1)+n_c}$
$P\left(X_2\mid C\right)=\frac{X_2+1}{\mathrm{Count}(X_2)+n_c}$

3.3 朴素贝叶斯模型的类型

$\begin{array}{ll}朴素贝叶斯模型& 数据类型\\ 伯努利模型& 二值(T/F)\\ 多项式模型& 离散值(如,计数)\\ 高斯模型& 连续值\end{array}$

不同朴素贝叶斯模型的区别，主要在于它们对概率分布$P(X_i|C)$所做的不同假设。

下面是相关类型的介绍，了解即可（来源：普通高中教科书 粤教版 信息技术 选择性必修4 人工智能初步 P60）

❗ 转载请注明出处
作者：HinsCoder
博客链接： 作者博客主页

3.4 结合不同的特征类型

问题：模型特征包含不同的数据类型（连续的和类别的）

解决方案：
方案1：将连续特征离散化成类别变量，然后应用多项式模型
方案2：用高斯模型拟合连续特征，用多项式模型拟合分类变量，然后再结合成一个“元模型”（后面章节会讲到）
(如特征$X_i$取连续值，假设p(X_i | C)~N($\mu ,{\sigma }^2$),根据训练样本数据估算$\mu ,{\sigma }^2$)

3.5 语法

导入包含朴素贝叶斯分类方法的类：

from sklearn.naive_bayes import BernoulliNB
# BernoulliNB：假设所有特征都符合BernoulliNB分布，其他还有MultinomialNB，GaussianNB(适用于特征值连续)等

创建该类的一个对象：

BNB = BernoulliNB(alpha=1.0) # 拉普拉斯平滑参数

拟合训练数据，并预测：

BNB = BNB.fit(X_train, y_train)  
y_predict = BNB.predict(X_test)

在线文档： 朴素贝叶斯的文档

BernoulliNB：假设所有特征都符合BernoulliNB分布，其他还有MultinomialNB，GaussianNB(适用于特征值连续)等

4. 支持向量机概述

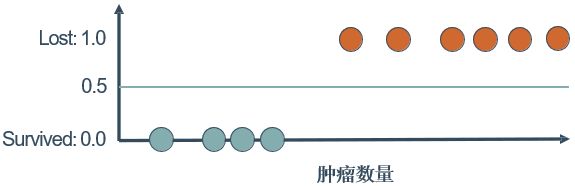
在逻辑回归那一篇中，我们提到过癌症病人治疗5年之后的状况的例子

从样本点数据（含N个特征x，标签y）的几何分布看，假如N维特征样本空间可以用线性平面（隐函数形式为$\omega x+b=0$，显函数形式$f(x)=\omega x+b$）分隔成两部分：

• $f(x)<0$，其中样本$i$均为负类（类别$y_i=-1$）
• $f(x)>0$，其中样本$i$均为正类（类别$y_i=1$）

则该平面称为分类超平面，分类任务即可描述为求该超平面（函数参数）问题，为线性可分问题。

而这个例子的特征向量为一维（样本点有1个特征），超平面可用隐函数$x+b=0$（(显函数形式$x=b$，形状为一个点）定义

如样本点有两个特征，则超平面可用隐函数${\omega }_1{x}_1+{\omega }_2{x}_2+b=0$（显函数形式$f(x)=w_1{x}_1+b$）定义。

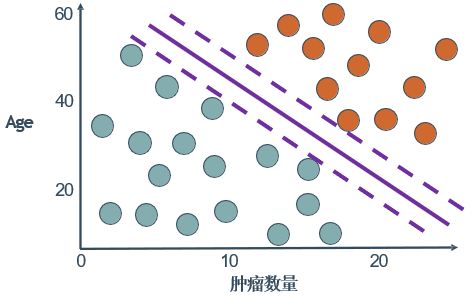
回到上面的例子，其中第③幅图无分类错误，但是否是最佳的分类位置？

可以看到结果未必，如果以后有新的样本加入，判断也会出问题。

那么这个分类边界应该怎么划分，才比较可靠呢？

答案就是：最大化类别之间的区域

Margin（间隔）r：定义为N个样本点到分类超平面的最小距离。根据平面几何知识可推得$X_i$到$f(x)=\omega x+b$的距离为$Margin(x_i)=\frac{f(x_i)}{(||\omega |{|}_2)}$，其中$||\omega |{|}_2$为向量$\omega$的L2长度（L2长度就是之前讲过的欧氏距离）。为了使得分类置信度高，间隔应最大，分类超平面应在两类正中间。离超平面最近的样本点称为支持向量，故分类器称为支持向量机。而其他样本点称为非支持向量。直观上，Margin越大，即“分类安全距离“越大，根据超平面分类结果越可靠。

我们将其推广到一般，假设分类超平面$f(x)={\omega }^{T}x+b$，样本空间中任意点$a$到超平面$(\omega ,b)$的距离可写为：
$$r=\frac{|{\omega }^{T}x+b|}{||\omega ||}$$
假设超平面$(\omega ,b)$能将训练样本正确分类，即对于$x_i,y_i\in D$，若$y_i+1$，则${\omega }^T{x}_i+b>0$；若$y_i=-1$，则有${\omega }^T{x}_i+b<0$。令
$\begin{array}{l}\{\begin{array}{l}{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩾+1,y_i=+1\\ {\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b⩽-1,y_i=-1\end{array}\end{array}$
两个异类支持向量到超平面的距离之和为：
$$\gamma =\frac{2}{\Vert \mathbf{w}\Vert }$$
它就是间隔，欲找到具有“最大间隔”(maximum margin)的划分超平面，也就是要找到能满足定义式中约束的参数$\omega$和$b$，使得$\gamma$最大，即
$$\begin{gathered} \underset{\mathbf{w},b}{\max }\frac{2}{\Vert \mathbf{w}\Vert } \\ \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m \end{gathered}$$
显然，为了最大化间隔，仅需最大化$\Vert \mathbf{w}{\Vert }^{-1}$，这等价于最小化$\Vert \mathbf{w}{\Vert }^2$。于是，式子可重写为
$$\begin{gathered} \underset{\mathbf{w},b}{\min }\frac{1}{2}\Vert \mathbf{w}{\Vert }^2 \\ \text{ s.t. }{y}_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩾1,i=1,2,\dots ,m \end{gathered}$$
这就是支持向量机的基本型。

求解分类平面参数的问题即为求约束条件下的极小值问题。先后采用拉格朗日乘法子和对偶算法，可将上述问题可转为非约束条件下的极值问题和对偶问题。

至于其中数学原理，大脑已宕机，不愿再展开~~

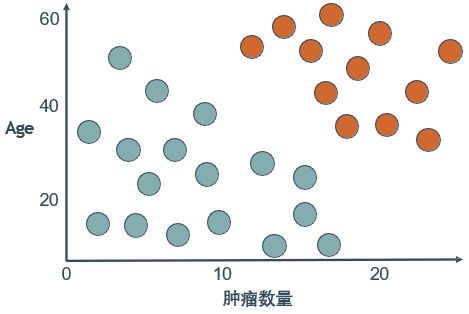
5. SVM分类

两个特征(nodes, age)
两类标签(survived, lost)

划分过程和前面类似

5.1 SVM对离群值的敏感性

实际应用中，这个划分边界可能并非这么好找，万一出现了离群点（outliers），那就变成下面这么划分吗？

显然是错误的，原来的划分线仍然是最优的选择

我们引入松弛因子（slack variables）这个概念，简单点说，就是让目标函数的约束不用那么强，即这个离群点不能套用正常的目标函数，其惩罚代价应该更大。

5.2 语法

导入包含分类方法的类：

from sklearn.svm import LinearSVC

创建该类的一个对象：

linSVC = LinearSVC(penalty='l2', C=10.0)	# 正则化参数，可用交叉验证调节

拟合训练数据，并预测测试数据：

linSVC = linSVC.fit(X_train, y_train)
y_predict = linSVC.predict(X_test)

在线文档： 线性SVM的语法

6. 核函数

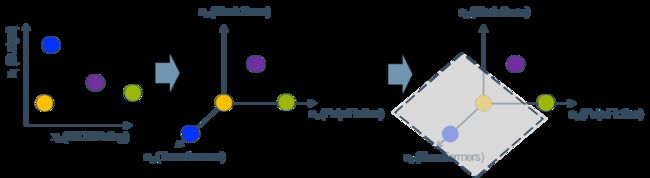
在前面的讨论中，我们假设训练样本是线性可分的，即存在一个划分超平面能将训练样本正确分类，然而在现实任务中，原始样本空间内也许并不存在一个能正确划分两类样本的超平面，我们就需要进行转化。方法是：将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分

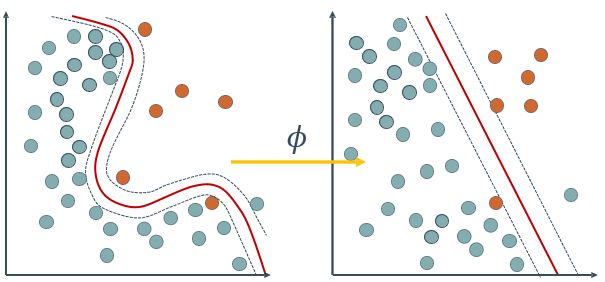
如下图，将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面。幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。

上面的处理方法称为核函数技巧（kernel trick）将数据从低维空间映射到高维空间的过程非常耗时，计算量很大。对低维空间的每个数据点（向量）进行这样的转换代价太大，需要寻找更加简单的处理办法。

举个具体的例子：

例如样本有特征$x_1,x_2$，非线性可分（决策边界为圆形），但升维$z=x_1^2+x_2^2$后，可用平面$Z=4$线性可分。

支持向量机模型，并不需要高维空间里的实际向量来进行最优平面的寻找，实际上，它仅仅需要向量之间的点积。这样就可以避免对数据进行实际的升维，想办法计算两个向量在高维空间中的点积即可。

核函数定义：对任意$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$，如$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)=<\Phi (x_i),\Phi (y_j)>$（向量积）算，则$\kappa ({\mathbf{x}}_i,{\mathbf{x}}_j)$为核函数。

6.1 常用核函数

$\begin{array}{lll}\text{ 名称 }& \text{ 表达式 }& \text{ 参数 }\\ \text{ 线性核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j& \\ \text{ 多项式核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left({\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j\right)}^d& d⩾1\text{ 为多项式的次数 }\\ \text{ 高斯核（RBF核） }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }^2}{2{\sigma }^2}\right)& \sigma >0\text{ 为高斯核的带宽(width) }\\ \text{ 拉普拉斯核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert }{\sigma }\right)& \sigma >0\\ \text{ Sigmoid 核 }& \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\tanh \left(\beta {\mathbf{x}}_i^{\mathrm{T}}{\mathbf{x}}_j+\theta \right)& \tanh \text{ 为双曲正切函数, }\beta >0,\theta <0\end{array}$

6.2 案例分析

金棕榈奖（Golden Palm Award）是法国戛纳国际电影节的最高奖项，创立于1957年，每年颁发一次。接下来我们需要根据样本分析金棕榈奖得主。

6.2.1 多项式核函数

通过提取一些高阶特征来转换数据.
Budget² + Rating² +Budget * Rating +…

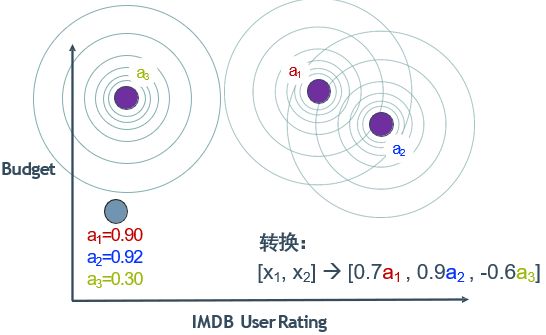
6.2.2 升维再分类

方法：使用高斯分布函数将样本空间（原特征2个）映射到新空间坐标系（新特征3个，原特征舍弃不用）。

6.2.3 高斯核函数

高斯（Radial Basis Function，RBF，又叫径向基）核函数

6.3 语法

6.3.1 使用核函数的SVM

导入包含分类方法的类：

from sklearn.svm import SVC

创建该类的一个对象：

rbfSVC = SVC(kernel='rbf', gamma=1.0, C=10.0)	# 设置核函数，及其相应参数(gamma)，C是错误项的惩罚力度

其中$\gamma =\frac{1}{2{\sigma }^2}$，$\gamma$越大，帽子越窄，决策平面附近影响决策平面的向量越少(或者说每个样本点仅产生较近距离的影响)，其权重越大，决策边界越崎岖曲折，模型越复杂，过大易过拟合。

拟合训练数据，并预测：

rbfSVC = rbfSVC.fit(X_train, y_train)
y_predict = rbfSVC.predict(X_test)

在线文档： 使用核函数的SVM的语法

用交叉验证调节核函数及其参数

6.3.2 快速核转换（了解）

问题：使用RBF核函数的SVM，在大量特征或数据时，训练速度非常慢，也就是特征过载。

解决：使用Nystroem或RBF sampler构建近似核映射，拟合一个线性分类器

Nystroem：
导入包含分类方法的类：

from sklearn.kernel_approximation import Nystroem

创建该类的一个对象：

nystroemSVC = Nystroem(kernel='rbf', gamma=1.0, n_components=100)	# 可以使用多种非线性核函数，kernel和gamma与SVC相同，n_components是样本量

拟合训练数据，并转换：

X_train = nystroemSVC.fit_transform(X_train)
X_test = nystroemSVC.transform(X_test)

使用交叉检验调节核参数和n_components

在线文档： Nystroem构建核映射的语法

RBF sampler：
导入包含分类方法的类：

from sklearn.kernel_approximation import RBFsampler

创建该类的一个对象：

rbfsample = RBFsampler(gamma=1.0, n_components=100)	# RBF 是唯一可用的核函数，参数名与前面的相同

拟合训练数据，并转换：

X_train = rbfsample.fit_transform(X_train)
X_test = rbfsample.transform(X_test)

使用交叉检验调节核参数和n_components
在线文档： RBFsampler构建核映射的语法

❗ 转载请注明出处
作者：HinsCoder
博客链接： 作者博客主页

7. SVM的参数优化

7.1 正则化参数C

正则化参数C，是错误项的惩罚系数，即对误差的宽容度。C越大，说明越不能容忍出现误差，容易过拟合；C越小，越容易欠拟合。C过大或过小，泛化能力均变差。选取恰当的C值，会对决策边界的平滑度和分类器对数据点分类的正确性进行折中平衡。

当采用更大的C时，分类器能够对更多的数据点进行正确分类，也就是对数据点的拟合程度更好，当然分类的决策边界也越来越曲里拐弯了，不是那么平滑。

所以需要对参数C进行选择，以便在平滑的决策边界和分类正确性之间折中。可以通过实验，在现有的数据集上获得更平滑的分类决策边界，避免过拟合，同时又达到较高的分类正确率。

7.2 gamma参数

gamma是选择径向基核函数之后，该函数自带的一个参数，隐含地决定了数据映射到新的特征空间后的分布。gamma值越大，支持向量越少；gamma值越小，支持向量越多。

gamma参数定义了在确定决策边界时，各个数据点的影响力到底有多远。如果gamma参数的值较小，则意味着每个数据点产生较远的影响，如果 gamma参数的值较大，意味着每个数据点产生较近距离的影响。

换句话说，如果gamma的值较大，那么决策边界依赖于决策边界附近的数据点，距离较远的数据点的影响力降低，甚至被直接忽略掉。由于更接近决策边界的数据点的权重更大，导致决策边界表现出曲里拐弯的特点。如果gamma参数的值较小，那么在确定决策边界的时候，把较远的数据点也考虑进来，分类的决策边界变得更加平滑。

参数gamma和C：

8. 综合案例：垃圾邮件识别

导入

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, confusion_matrix, f1_score

读取csv文件，把csv文件读到一个Pandas 的 DataFrame对象里。然后对数据里面的NULL值，用空字符串，即’ '来代替。

原始csv文件如下：

df1=pd.read_csv("spamham.csv")
df=df1.where((pd.notnull(df1)), '')

对Category列进行变换，将取值ham（垃圾邮件）和 spam（非垃圾邮件）分别改成1或者0，以便进行后续机器学习模型的训练。

df.loc[df["Category"] == 'ham', "Category"]=1
df.loc[df["Category"] == 'spam', "Category"]=0

把Message列作为x，Category 列作为y。

df_x=df['Message']
df_y=df['Category']

把x和y划分成训练集和测试集，分别占原有数据集的80%和20%。

x_train, x_test, y_train, y_test=train_test_split(df_x, df_y, test_size=0.2)

把 Message数据列，也就是x的文本转换成机器学习的特征值。在这里采用文本的TF-IDF特征，TF表示单个文档里的某个词项的频率，IDF表示整个文集中词项的逆文档频率。IDF把在很多文档中都出现的但对于文档的类别划分没有太多贡献的词项的重要性降低。

tfvec=TfidfVectorizer(min_df=1, stop_words='english', lowercase=True)	# 最小是一个单词、文本是英文、全部转为小写
x_trainFeat=tfvec.fit_transform(x_train)
x_testFeat=tfvec.transform(x_test)

创建朴素贝叶斯分类模型，对其进行训练，并且利用模型对测试集进行预测。

# 多项式模型，x_trainFeat中特征(词)元素值表示词频信息，假设其满足多项式分布
y_trainGnb=y_train.astype('int')
classifierModel=MultinomialNB()
classifierModel.fit(x_trainFeat, y_trainGnb)
y_pred=classifierModel.predict(x_testFeat)

把测试集的y转换成整数形式，对上述模型的预测值进行比较，显示分类器的精度、F1分数，以及混淆矩阵。

y_test=y_test.astype('int')
print("Accuracy Score: {0:.4f}".format(accuracy_score(y_test, y_pred)*100))
print("F1 Score:{0: .4f}".format(f1_score(y_test, y_pred, average='macro')*100))
print("Confusion matrix:")
print(confusion_matrix(y_test, y_pred))

$$\begin{gathered} \text{Accuracy Score}：97.2197 \\ \text{F1 Score}:93.2741 \\ \text{Confusion matrix}: \\ [[11531] \\ [0969]] \end{gathered}$$

可以从两个方面改善上述模型，进一步提高分类器的分类准确率：
（1）词形还原。把一个单词的不同词形还原为基本形式。比如election，elections，elected 等，应该还原成elect，从而把它们看作相同的单词，有利于文本的正确分析。
（2）使用N-Gram作为文本分类的特征（分类器的输入)。连在一起的两个单词称为2-Gram；连在一起的三个单词称为3-Gram，它们携带了语句中单词的前后关系。可以使用连在一起的两个单词，比如“clean match”"close election”的频率作为文档特征。

我们可以再试一下高斯模型

# 高斯模型，与多项式模型比较，结果相同
from sklearn.naive_bayes import GaussianNB
classifierModel2=GaussianNB()
classifierModel2.fit(x_trainFeat.toarray),y_trainGnb)
# GaussianNB(priors=None)
y _pred2=classifierModel.predict(x_testFeat)
print("Accuracy Score: {0:.4f}".format(accuracy_score(y_test，y _pred2)*100))
print("F1 Score:{0:.4f}".format(fl_score(y_test,y _pred2,average='macro')*100))
print("Confusion matrix:")
print (confusion_matrix(y_test,y_pred2))

$$\begin{gathered} \text{Accuracy Score}：97.2197 \\ \text{F1 Score}:93.7645 \\ \text{Confusion matrix}: \\ [[12731] \\ [0957]] \end{gathered}$$

为了把文本进行向量化，首先建立一个字典表，字典表的大小为N。然后针对每个文本，把它转换成N维向量，向量的每个分量根据文本里出现单词的频率来决定。出现某个单词，相应的分量就记为单词的频率；如果不出现，相应的分量就记为0。这种方法把每个文本看作a Bag of Words(称为BOW方法)，对于每个出现的单词，都看作文本的一个特征，每个特征的具体取值为单词的频率。比如，对于句子“AlImonkeys are primates but not all primates are monkeys”，单词monkeys出现的频率为2/10，单词but出现的频率为1/10。

使用词频表示每个单词会带来一系列问题，更为合理的是TF-IDF表示法，即不仅考虑单词在文档中出现的频率，还用逆文档频率来衡量每个单词的重要程度。

为了提高分类器的正确率、召回率等关键指标，有时候需要对文本进行预处理，包括剔除停用词、词干分析、词根分析、使用n-gram特征等，更加详细的信息请参考相关资料。

现在每个文本被转换成一个向量，这个向量具有成千甚至上万个分量，每个分量表示文本中出现某个单词的频率。一系列的文本经过这种转换后，形成了一系列的样本，加上文本的标注信息，比如文本是否垃圾邮件、文本是正面情感还是负面情感等，就可以用来训练支持向量机分类模型。

创建支持向量机模型，对其进行训练，并且利用模型对测试集进行预测。

from sklearn.svm import LinearSVC
y_trainSvm=y_train.astype('int')
classifierModel=LinearSVC()
classifierModel.fit(x_trainFeat, y_trainSvm)
predResult=classifierModel.predict(x_testFeat)

把测试集的y转换成整数形式，对上述模型的预测值进行比较，显示分类器的精度、F1，以及混淆矩阵。

y_test=y_test.astype('int')
print("Accuracy Score:{0:.4f}".format(accuracy_score(y_test, predResult)*100))

print("F1 Score:{0: .4f}".format(f1_score(y_test, predResult, average='macro')*100))
cmMNb=confusion_matrix(y_test, predResult)
print("Confusion matrix:")
print(cmMNb)

$$\begin{gathered} \text{Accuracy Score}：98.2960 \\ \text{F1 Score}:95.7351 \\ \text{Confusion matrix}: \\ [[11613] \\ [6980]] \end{gathered}$$

可以看到，在这个垃圾邮件识别任务中，支持向量机模型获得了比朴素贝叶斯模型更好的预测效果。

9. 逻辑回归VS支持向量机

联系：

• 都是监督的分类算法。
• 都是线性分类方法 (不考虑核函数时）。
• 都是判别模型。

区别：

• 损失函数的不同，LR是对数损失函数，SVM是hinge损失函数。
• SVM不能产生概率，LR可以产生概率。
• SVM自带结构风险最小化，LR则是经验风险最小化。
• SVM可以用核函数，而LR一般不用核函数。

• 判别模型：由数据直接学习决策函数Y=f(X)，或者由条件概率分布P(Y|X)作为预测模型。判别方法关心的是给定输入X，应该预测出什么样的输出Y。SVM、LR、KNN、决策树都是判别模型。
• 生成模型：由数据学习联合概率密度分布P(X,Y)，然后求出条件概率分布P(Y|X)。生成方法关心的是给定输入X产生输出Y的生成关系。朴素贝叶斯、隐马尔可夫模型等是生成模型。
• 经验风险：对所有训练样本都求一次损失函数，再累加求平均。即模型对训练样本中所有样本的预测能力。
• 期望风险：对所有样本（包含未知样本和已知的训练样本）的预测能力，是全局概念。（经验风险则是局部概念，仅表示决策函数对训练数据集里样本的预测能力。）
• 结构风险：对经验风险和期望风险的折中。结构风险在经验风险的基础上加上表示模型复杂度的正则化项或惩罚项。

9.1 选用策略

$\begin{array}{lll}\text{ 特征 }& \text{ 数据 }& \text{ 选择模型 }\\ \text{ 大量 ( 10K特征) }& \text{ 少量 (1K 行) }& \text{ 简单, 逻辑回归或LinearSVC }\\ \text{ 少量 }(<100\text{ 特征 })& \text{ 中等 }(\sim 10\mathrm{k}\text{ 行 })& \text{ 带RBF核函数的SVC }\\ \text{ 少量 }(<100\text{ 特征) }& \text{ 大量 ( }>100\mathrm{K}\text{ 行) }& \text{ 增加特征, 逻辑回归, LinearSVC 或者核近似 }\end{array}$

10. 课后习题

1. 【单选题】关于朴素贝叶斯分类器的说法，以下说法错误的是（）
   A. 朴素贝叶斯分类器需假设特征变量间相互独立(即样本的所有特征之间相互不相关)。
   B. 如某测试样本的特征变量的取值未在训练集中出现，依朴素贝叶斯算法所有可能分类的概率均为0。对此类零概率问题，朴素贝叶斯分类器一般通过平滑技术(如拉普拉斯平滑技术)加以处理。
   C. 朴素贝叶斯分类器无法对含有连续数值型特征的样本数据进行分类。
   D. 朴素贝叶斯分类器是基于贝叶斯定理的机器学习算法。贝叶斯定理：$P(C|X)=P(X|C)P(C)/P(X)$，在实际应用中，对输入样本$X$，要比较$X$对每一个可能类型$C_i$的后验概率$P_i$，取其中$P_i$最大的类型$C_i$为其预测结果。

2. 【单选题】有一批训练样本数据如下，从训练样本训练朴素贝叶斯分类器，分类器学习采用了拉普拉斯平滑技术（拉普拉斯平滑系数=1）。
   $\begin{array}{ccccc}\text{ 肤色 }& \text{ 脸型 }& \text{ 身高 }& \text{ 体重 }& \text{ 入选 }\\ \text{ 白 }& \text{ 长条 }& \text{ 高 }& \text{ 中等 }& \text{ 否 }\\ \text{ 较白 }& \text{ 方形 }& \text{ 较高 }& \text{ 重 }& \text{ 否 }\\ 黑& 圆形& 较矮& 较重& 是\\ \text{ 白 }& \text{ 鹅蛋形 }& \text{ 中等 }& \text{ 重 }& \text{ 否 }\\ 较黑& 圆形& 矮& 较重& 是\\ \text{ 白 }& \text{ 圆形 }& \text{ 高 }& \text{ 重 }& \text{ 否 }\\ \text{ 黄 }& \text{ 方形 }& \text{ 较高 }& \text{ 较轻 }& \text{ 否 }\\ 白& 圆形& 较矮& 重& 是\\ \text{ 较黄 }& \text{ 鹅蛋形 }& \text{ 中等 }& \text{ 轻 }& \text{ 否 }\end{array}$
   现根据某待测样本的特征（肤色=较黑，脸型=圆形，身高=中等，体重=重）预测该样本是否能入选，以下对分类器预测该样本入选结果的描述，正确的是( )
   A. 入选=是
   B. 入选=否
   C. 入选=是与入选=否的可能性均不为0，无法判定哪个可能性更大
   D. 入选=是与入选=否的可能性均为0

3. 【单选题】收集到一批(共1000个)水果样本数据，每个样本数据包括水果类型(香蕉、橘子、其他水果)和水果特征(是否长条、味道是否甜、颜色是否黄色)信息。现将这1000个样本的数据分特征和类别统计汇总，记录如下：
   $\begin{array}{ccccc}\text{ 水果类型 }& \text{ 总个数 }& \text{ 形状为长条（个，L） }& \text{ 味道甜（个，S） }& \text{ 颜色为黄色（个，Y） }\\ \text{ 香蕉（B） }& 500& 400& 350& 450\\ \text{ 橘子（O） }& 300& 0& 150& 250\\ \text{ 其他（T） }& 200& 100& 150& 50\\ \text{ 合计 }& 1000& 500& 650& 750\end{array}$
   以该批数据训练一个朴素贝叶斯分类器对水果分类。现有一个水果，形状为非长条、味道甜且颜色为非黄色，如用以上训练出的朴素贝叶斯分类器预测其类别，预测结果应为( )
   A. 香蕉
   B. 橘子
   C. 其他水果
   D. 无法判定

1.C（解析：如高斯模型） 2.A（解析：$P(是)=\frac{1+1}{6+3}\times \frac{3+1}{4+3}\times \frac{0+1}{5+3}\times \frac{1+1}{5+3}=\frac{1}{252}\approx 0.00397$；$P(否)=\frac{0+1}{6+6}\times \frac{1+1}{4+6}\times \frac{2+1}{5+6}\times \frac{3+1}{5+6}=\frac{1}{605}\approx 0.00165$，因此，结果是入选）
3.C（解析：参考上面的打网球案例计算$\begin{array}{ccccc}& \text{ 非长条 }& \text{ 甜 }& \text{ 非黄色 }& \text{ 概率 }\\ \text{ 香蕉（B） }& 100& 350& 50& 0.014\\ \text{ 橘子（O） }& 300& 150& 50& 0.083333\\ \text{ 其他（T） }& 100& 150& 150& 0.28125\end{array}$）

---

OK，以上就是本期知识点“朴素贝叶斯与支持向量机”的知识啦~~ ，感谢友友们的阅读。后续还会继续更新，欢迎持续关注哟~
如果有错误❌，欢迎批评指正呀~让我们一起相互进步
如果觉得收获满满，可以点点赞支持一下哟~

❗ 转载请注明出处
作者：HinsCoder
博客链接： 作者博客主页