R语言聚类分析——代码解析

+（1）实验数据：iris鸢尾花数据

datd(iris)

head(iris)

  Sepal.Length         Sepal.Width         Petal.Length          Petal.Width                Species
1          5.1                         3.5                  1.4                         0.2                          setosa
2          4.9                         3.0                  1.4                         0.2                          setosa
3          4.7                         3.2                  1.3                         0.2                          setosa
4          4.6                         3.1                  1.5                         0.2                          setosa
5          5.0                         3.6                  1.4                         0.2                          setosa
6          5.4                         3.9                  1.7                         0.4                          setosa

data()函数载入数据集

head()函数查看前几行数据，括号内填前多少行，默认6行

table(iris$Species)

 setosa versicolor  virginica 
        50         50         50 

table()函数查看"Species"三种值出现的次数

set.seed(1234)

kmeansObj <-kmeans(iris[,-5],centers=3)

print(kmeansObj)

K-means clustering with 3 clusters of sizes 50, 62, 38

Cluster means:
  Sepal.Length Sepal.Width Petal.Length Petal.Width
1     5.006000    3.428000     1.462000    0.246000
2     5.901613    2.748387     4.393548    1.433871
3     6.850000    3.073684     5.742105    2.071053

Clustering vector:
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [37] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [73] 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3
[109] 3 3 3 3 3 2 2 3 3 3 3 2 3 2 3 2 3 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3
[145] 3 3 2 3 3 2

Within cluster sum of squares by cluster:
[1] 15.15100 39.82097 23.87947
 (between_SS / total_SS =  88.4 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"    
[5] "tot.withinss" "betweenss"    "size"         "iter"        
[9] "ifault" 

set.seed(1234)：设置随机数种子，使得实验结果可复制。括号内的数值是随意的，就是对抽取的随机数进行标记。在下一次可抽取出相同的样本。

kmeans()：做K均值聚类。

第一个参数，是数据集，这里使用切片的方法来提取数据，这样可以去掉类别Species。

这里讲一下切片吧

df[，]，默认所以，全部，[,]表示  [行,列]

df[1，]，取第一行，所以列

df[，1]，取所有行，第一列

df[-1，]，删取第一行后，再取所有的列

df[，-1]，删除第一列后，再取所有的行

第二个参数centers，表示簇的数量，即多少类，设置为3

其他参数在最后介绍

下面对输出的结果进行解析：

（1）K-means clustering with 3 clusters of sizes 50, 62, 38

表示三组的K-均值聚类的分类情况，第一个类为50个样本，第二个有62个样本，第三有38个样本。

（2）Cluster means:

每个聚类中各个列值生成的最终平均值

（3）Clustering vector:

每行记录所属的聚类(2代表属于第二个聚类，1代表属于第一个聚类，3代表属于第三个聚类)

（4）Within cluster sum of squares by cluster:

每个聚类内部的距离平方和

（5）Available components:

运行kmeans函数返回的对象所包含的各个组成部分

（6）Available components:

运行kmeans函数返回的对象所包含的各个组成部分

部分的含义：

“cluster”是一个整数向量，用于表示记录所属的聚类

“centers”是一个矩阵，表示每聚类中各个变量的中心点

“totss”表示所生成聚类的总体距离平方和

“withinss”表示各个聚类组内的距离平方和

“tot.withinss”表示聚类组内的距离平方和总量

“betweenss”表示聚类组间的聚类平方和总量

“size”表示每个聚类组中成员的数量
 

那我们如何查看呢？

如：

kmeansObj$totss

kmeansObj$betweenss

即可进行查看

还有以上的数值是如何计算的呢？

（查过很多资料，都没有说是如何计算的，只有字面意思解释，那不行啊）

以上的案例数据太大不好介绍

接下来，我使用一个简单的数据集来解释，让字面意思更清晰

> df <- data.frame(x=c(0,0,1.5,5,5),y=c(2,0,0,0,2))
> km <- kmeans(df[,-2],centers=2)
> print(km)

输出：

K-means clustering with 2 clusters of sizes 3, 2

Cluster means:
  [,1]
1  0.5
2  5.0

Clustering vector:
[1] 1 1 1 2 2

Within cluster sum of squares by cluster:
[1] 1.5 0.0
 (between_SS / total_SS =  94.2 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"

> print(df)
    x         y
1  0.0      2
2  0.0      0
3  1.5      0
4  5.0      0
5  5.0      2

解释：

K-means clustering with 2 clusters of sizes 3, 2

使用K-means算法以2为参数，把5个数据对象分为2个聚类，确保聚类具有较高的相似度，而聚类间的相似度较低。

首先使用欧几里得定理来分类：求出5个类的距离

1与2的距离：0

1与3的距离：1.5

1与4的距离：5

1与5的距离：5

2与3的距离：1.5

2与4的距离：5

2与5的距离：5

3与4的距离：3.5

3与5的距离：3.5

4与5的距离：0

要分成两类，所以1与2一类，4和5一类，3到1、2为1.5，到4、5为3.5，所以和1、2、一类

C1（1、2、3），C2（4，5）

Cluster means:
  [,1]
1  0.5
2  5.0

每个聚类中各个列值生成的最终平均值

1:

2:

Within cluster sum of squares by cluster:
[1] 1.5 0.0

每个聚类内部的距离平方和

1.5：什么意思呢？就是1、2相同到3的距离的平方和

0.0：4到5的距离为0

（4）评估k均值聚类结果

table(kmeansObj$cluster,iris$Species)
    setosa versicolor virginica
  1     50          0         0
  2      0         48        14
  3      0          2        36

这个与混淆矩阵差不多，差别是这里真实的是列的，预测的是行的

（5）可视化k均值聚类结果

par(mar=c(4,4,0.1,0.1))

plot(iris[c("Petal.Width","Sepal.Width")],col = kmeansObj$cluster)

points(kmeansObj$centers[,c("Petal.Width","Sepal.Width")],col =1:3,pch=8,cex=2)

par()函数设置绘图参数

mar参数：图形边距参数（下，左，上，右）

plot()函数画散点图

col参数：符号和颜色，这里把聚类放入表示表示三种颜色类型

points()添加点并设置属性

 (6)做层次聚类

set.seed(1234)

 idx <- sample(1:dim(iris)[1],40)

 irisSample <-iris[idx,]

hc <-hclust(dist(irisSample[,-5]),method = "average")

print(hc)

Call:
hclust(d = dist(irisSample[, -5]), method = "average")

Cluster method   : average 
Distance         : euclidean 
Number of objects: 40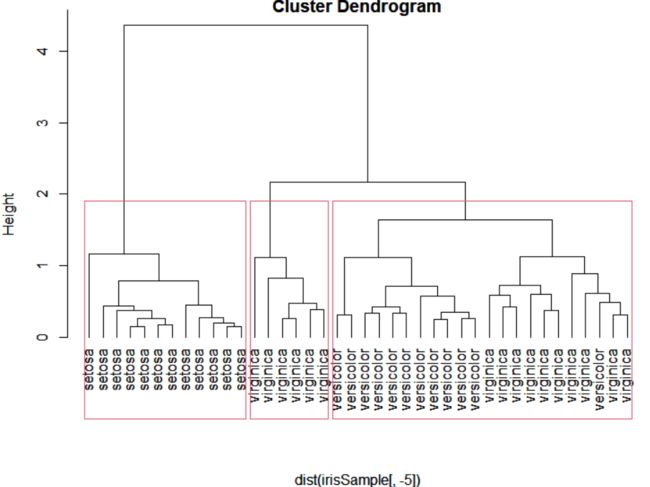 

groups <- cutree(hc,k = 3)

table(groups,iris$Species[idx])

groups setosa versicolor virginica
     1     12          0         0
     2      0         12        10
     3      0           0         6