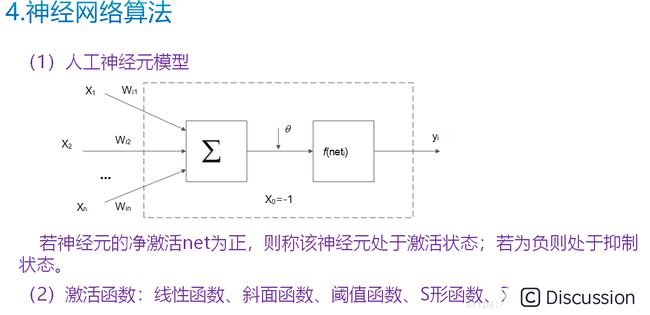
【预测模型】BP神经网络的预测
- 原理
clear; clc; TestSamNum = 20; % 学习样本数量 ForcastSamNum = 2; % 预测样本数量 HiddenUnitNum=8; % 隐含层 InDim = 3; % 输入层 OutDim = 2; % 输出层 % 原始数据 % 人数(单位:万人) sqrs = [20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 ... 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63]; % 机动车数(单位:万辆) sqjdcs = [0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6... 2.7 2.85 2.95 3.1]; % 公路面积(单位:万平方公里) sqglmj = [0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 ... 0.56 0.59 0.59 0.67 0.69 0.79]; % 公路客运量(单位:万人) glkyl = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 ... 22598 25107 33442 36836 40548 42927 43462]; % 公路货运量(单位:万吨) glhyl = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 ... 13320 16762 18673 20724 20803 21804]; p = [sqrs; sqjdcs; sqglmj]; % 输入数据矩阵 t = [glkyl; glhyl]; % 目标数据矩阵 [SamIn, minp, maxp, tn, mint, maxt] = premnmx(p, t); % 原始样本对(输入和输出)初始化 SamOut = tn; % 输出样本 MaxEpochs = 50000; % 最大训练次数 lr = 0.05; % 学习率 E0 = 1e-3; % 目标误差 rng('default'); W1 = rand(HiddenUnitNum, InDim); % 初始化输入层与隐含层之间的权值 B1 = rand(HiddenUnitNum, 1); % 初始化输入层与隐含层之间的阈值 W2 = rand(OutDim, HiddenUnitNum); % 初始化输出层与隐含层之间的权值 B2 = rand(OutDim, 1); % 初始化输出层与隐含层之间的阈值 ErrHistory = zeros(MaxEpochs, 1); for i = 1 : MaxEpochs HiddenOut = logsig(W1*SamIn + repmat(B1, 1, TestSamNum)); % 隐含层网络输出 NetworkOut = W2*HiddenOut + repmat(B2, 1, TestSamNum); % 输出层网络输出 Error = SamOut - NetworkOut; % 实际输出与网络输出之差 SSE = sumsqr(Error); % 能量函数(误差平方和) ErrHistory(i) = SSE; if SSE < E0 break; end % 以下六行是BP网络最核心的程序 % 权值(阈值)依据能量函数负梯度下降原理所作的每一步动态调整量 Delta2 = Error; Delta1 = W2' * Delta2 .* HiddenOut .* (1 - HiddenOut); dW2 = Delta2 * HiddenOut'; dB2 = Delta2 * ones(TestSamNum, 1); dW1 = Delta1 * SamIn'; dB1 = Delta1 * ones(TestSamNum, 1); % 对输出层与隐含层之间的权值和阈值进行修正 W2 = W2 + lr*dW2; B2 = B2 + lr*dB2; % 对输入层与隐含层之间的权值和阈值进行修正 W1 = W1 + lr*dW1; B1 = B1 + lr*dB1; end HiddenOut = logsig(W1*SamIn + repmat(B1, 1, TestSamNum)); % 隐含层输出最终结果 NetworkOut = W2*HiddenOut + repmat(B2, 1, TestSamNum); % 输出层输出最终结果 a = postmnmx(NetworkOut, mint, maxt); % 还原网络输出层的结果 x = 1990 : 2009; % 时间轴刻度 newk = a(1, :); % 网络输出客运量 newh = a(2, :); % 网络输出货运量 subplot(2, 1, 1); plot(x, newk, 'r-o', x, glkyl, 'b--+'); legend('网络输出客运量', '实际客运量'); xlabel('年份'); ylabel('客运量/万人'); subplot(2, 1, 2); plot(x, newh, 'r-o', x, glhyl, 'b--+'); legend('网络输出货运量', '实际货运量'); xlabel('年份'); ylabel('货运量/万吨'); % 利用训练好的网络进行预测 pnew=[73.39 75.55 3.9635 4.0975 0.9880 1.0268]; % 2010年和2011年的相关数据; pnewn = tramnmx(pnew, minp, maxp); HiddenOut = logsig(W1*pnewn + repmat(B1, 1, ForcastSamNum)); % 隐含层输出预测结果 anewn = W2*HiddenOut + repmat(B2, 1, ForcastSamNum); % 输出层输出预测结果 anew = postmnmx(anewn, mint, maxt); disp('预测值d:'); disp(anew);
最近一段时间在研究如何利用预测其销量个数,在网上搜索了一下,发现了很多模型来预测,比如利用回归模型、时间序列模型,GM(1,1)模型,可是自己在结合实际的工作内容,发现这几种模型预测的精度不是很高,于是再在网上进行搜索,发现神经网络模型可以来预测,并且有很多是结合时间序列或者SVM(支持向量机)等组合模型来进行预测,本文结合实际数据,选取了常用的BP神经网络算法,其算法原理,因网上一大堆,所以在此不必一一展示,并参考了bp神经网络进行交通预测的Matlab源代码这篇博文,运用matlab 2016a,给出了下面的代码,并最终进行了预测
clc
clear all
close all
%bp 神经网络的预测代码
%载入输出和输入数据
load C:\Users\amzon\Desktop\p.txt;
load C:\Users\amzon\Desktop\t.txt;
%保存数据到matlab的工作路径里面
save p.mat;
save t.mat;%注意t必须为行向量
%赋值给输出p和输入t
p=p;
t=t;
%数据的归一化处理,利用mapminmax函数,使数值归一化到[-1.1]之间
%该函数使用方法如下:[y,ps] =mapminmax(x,ymin,ymax),x需归化的数据输入,
%ymin,ymax为需归化到的范围,不填默认为归化到[-1,1]
%返回归化后的值y,以及参数ps,ps在结果反归一化中,需要调用
[p1,ps]=mapminmax(p);
[t1,ts]=mapminmax(t);
%确定训练数据,测试数据,一般是随机的从样本中选取70%的数据作为训练数据
%15%的数据作为测试数据,一般是使用函数dividerand,其一般的使用方法如下:
%[trainInd,valInd,testInd] = dividerand(Q,trainRatio,valRatio,testRatio)
[trainsample.p,valsample.p,testsample.p] =dividerand(p,0.7,0.15,0.15);
[trainsample.t,valsample.t,testsample.t] =dividerand(t,0.7,0.15,0.15);
%建立反向传播算法的BP神经网络,使用newff函数,其一般的使用方法如下
%net = newff(minmax(p),[隐层的神经元的个数,输出层的神经元的个数],{隐层神经元的传输函数,输出层的传输函数},'反向传播的训练函数'),其中p为输入数据,t为输出数据
%tf为神经网络的传输函数,默认为'tansig'函数为隐层的传输函数,
%purelin函数为输出层的传输函数
%一般在这里还有其他的传输的函数一般的如下,如果预测出来的效果不是很好,可以调节
%TF1 = 'tansig';TF2 = 'logsig';
%TF1 = 'logsig';TF2 = 'purelin';
%TF1 = 'logsig';TF2 = 'logsig';
%TF1 = 'purelin';TF2 = 'purelin';
TF1='tansig';TF2='purelin';
net=newff(minmax(p),[10,1],{TF1 TF2},'traingdm');%网络创建
%网络参数的设置
net.trainParam.epochs=10000;%训练次数设置
net.trainParam.goal=1e-7;%训练目标设置
net.trainParam.lr=0.01;%学习率设置,应设置为较少值,太大虽然会在开始加快收敛速度,但临近最佳点时,会产生动荡,而致使无法收敛
net.trainParam.mc=0.9;%动量因子的设置,默认为0.9
net.trainParam.show=25;%显示的间隔次数
% 指定训练参数
% net.trainFcn = 'traingd'; % 梯度下降算法
% net.trainFcn = 'traingdm'; % 动量梯度下降算法
% net.trainFcn = 'traingda'; % 变学习率梯度下降算法
% net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法
% (大型网络的首选算法)
% net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小
% 共轭梯度算法
% net.trainFcn = 'traincgf'; %Fletcher-Reeves修正算法
% net.trainFcn = 'traincgp'; %Polak-Ribiere修正算法,内存需求比Fletcher-Reeves修正算法略大
% net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大
% (大型网络的首选算法)
%net.trainFcn = 'trainscg'; % ScaledConjugate Gradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多
% net.trainFcn = 'trainbfg'; %Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快
% net.trainFcn = 'trainoss'; % OneStep Secant Algorithm,计算量和内存需求均比BFGS算法小,比共轭梯度算法略大
% (中型网络的首选算法)
%net.trainFcn = 'trainlm'; %Levenberg-Marquardt算法,内存需求最大,收敛速度最快
% net.trainFcn = 'trainbr'; % 贝叶斯正则化算法
% 有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss', 'trainlm'
%在这里一般是选取'trainlm'函数来训练,其算对对应的是Levenberg-Marquardt算法
net.trainFcn='trainlm';
[net,tr]=train(net,trainsample.p,trainsample.t);
%计算仿真,其一般用sim函数
[normtrainoutput,trainPerf]=sim(net,trainsample.p,[],[],trainsample.t);%训练的数据,根据BP得到的结果
[normvalidateoutput,validatePerf]=sim(net,valsample.p,[],[],valsample.t);%验证的数据,经BP得到的结果
[normtestoutput,testPerf]=sim(net,testsample.p,[],[],testsample.t);%测试数据,经BP得到的结果
%将所得的结果进行反归一化,得到其拟合的数据
trainoutput=mapminmax('reverse',normtrainoutput,ts);
validateoutput=mapminmax('reverse',normvalidateoutput,ts);
testoutput=mapminmax('reverse',normtestoutput,ts);
%正常输入的数据的反归一化的处理,得到其正式值
trainvalue=mapminmax('reverse',trainsample.t,ts);%正常的验证数据
validatevalue=mapminmax('reverse',valsample.t,ts);%正常的验证的数据
testvalue=mapminmax('reverse',testsample.t,ts);%正常的测试数据
%做预测,输入要预测的数据pnew
pnew=[313,256,239]';
pnewn=mapminmax(pnew);
anewn=sim(net,pnewn);
anew=mapminmax('reverse',anewn,ts);
%绝对误差的计算
errors=trainvalue-trainoutput;
%plotregression拟合图
figure,plotregression(trainvalue,trainoutput)
%误差图
figure,plot(1:length(errors),errors,'-b')
title('误差变化图')
%误差值的正态性的检验
figure,hist(errors);%频数直方图
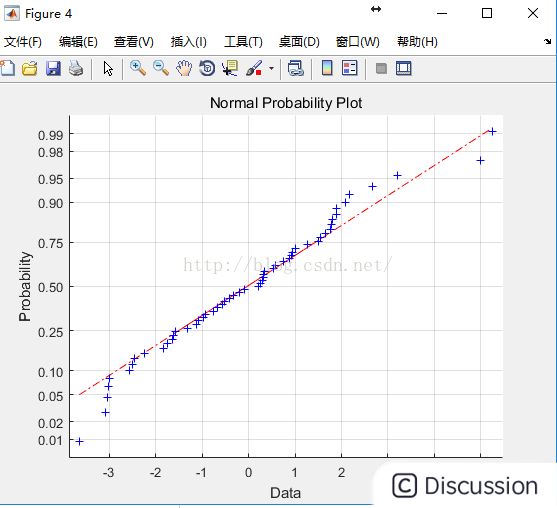
figure,normplot(errors);%Q-Q图
[muhat,sigmahat,muci,sigmaci]=normfit(errors); %参数估计 均值,方差,均值的0.95置信区间,方差的0.95置信区间
[h1,sig,ci]= ttest(errors,muhat);%假设检验
figure, ploterrcorr(errors);%绘制误差的自相关图
figure, parcorr(errors);%绘制偏相关图
运行之后的,结果如下:
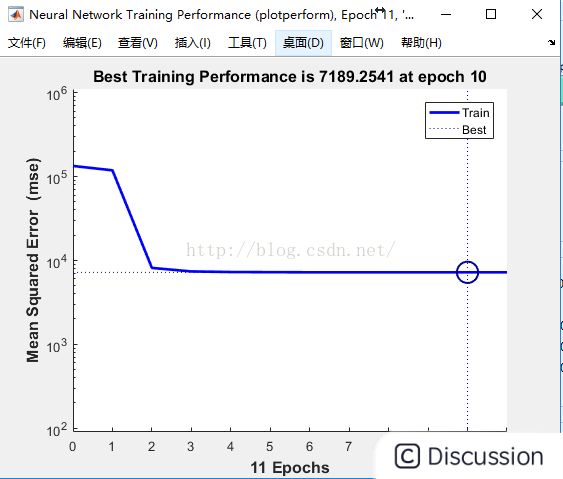
BP神经网络的结果分析图
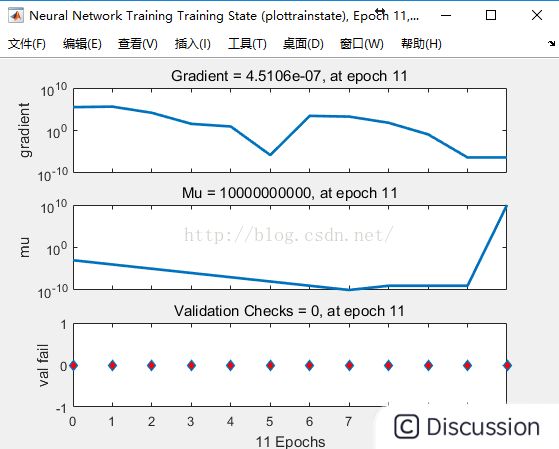
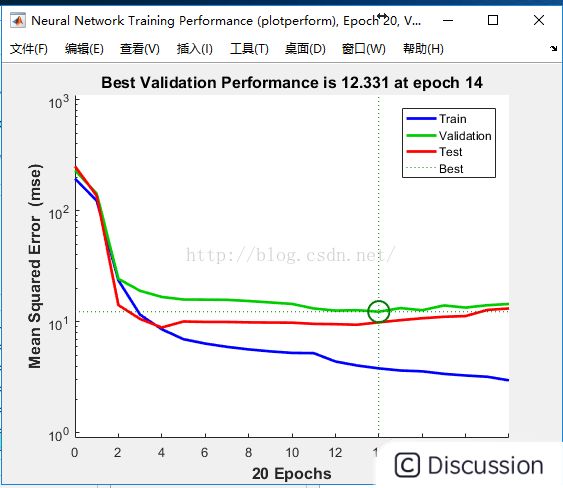
训练数据的梯度和均方误差之间的关系图
验证数据的梯度与学习次数
残差的正态的检验图(Q-Q图)
在网上,发现可以通过神经网络工具箱这个GUI界面来创建神经网络,其一般的操作步骤如下:
1:在输入命令里面输入nntool命令,或者在应用程序这个选项下找到Netrual Net Fitting 这个应用程序,点击打开,就能看见如下界面
2:输入数据和输出数据的导入(在本文中选取了matlab自带的案例数据)
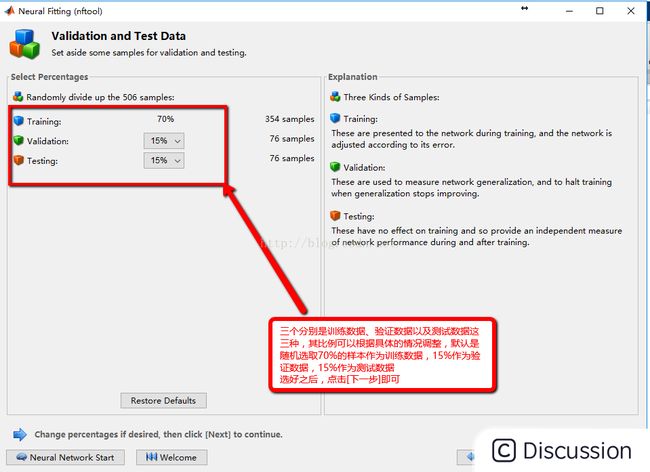
\ 3:随机选择三种类型的数据所占的样本量的比例,一般选取默认即可\
\ \ 4:隐层神经元的确定 \ \ 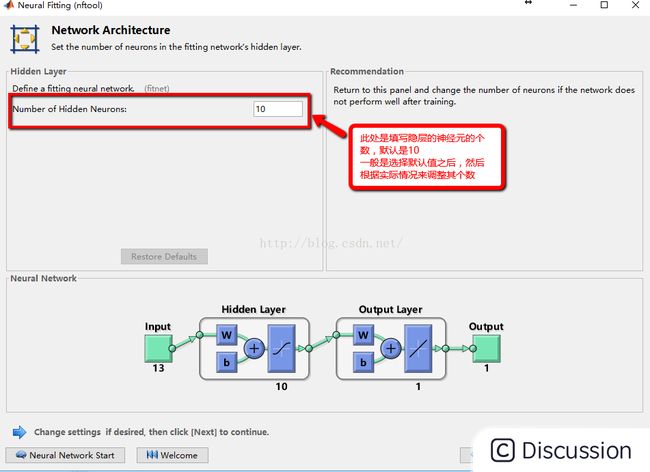 \ \ 5:训练算法的选取,一般是选择默认即可,选择完成后点击\ 按钮即可运行程序 \ \
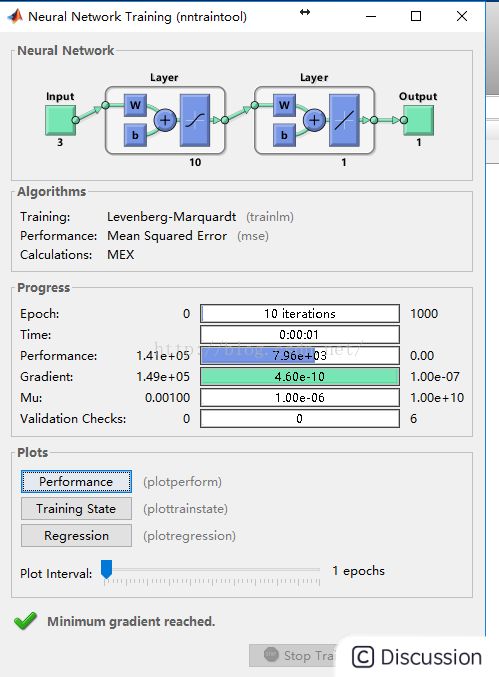
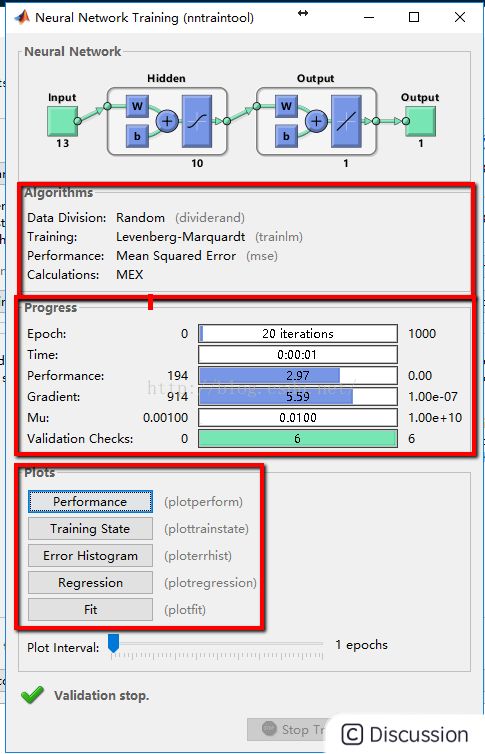
\ \ 5:训练算法的选取,一般是选择默认即可,选择完成后点击\ 按钮即可运行程序 \ \  \ \ \ 6:根据得到的结果,一般是MSE的值越小,R值越接近1,其训练的效果比较,并第二张图给出了神经网络的各参数的设置以及其最终的结果,其拟合图R越接近1,模型拟合的更好\ \
\ \ \ 6:根据得到的结果,一般是MSE的值越小,R值越接近1,其训练的效果比较,并第二张图给出了神经网络的各参数的设置以及其最终的结果,其拟合图R越接近1,模型拟合的更好\ \ 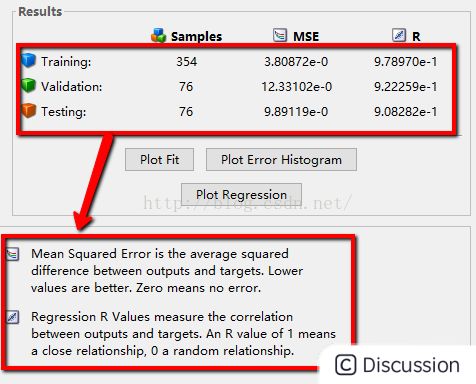 \ \
\ \  \ \
\ \  \ \
\ \ 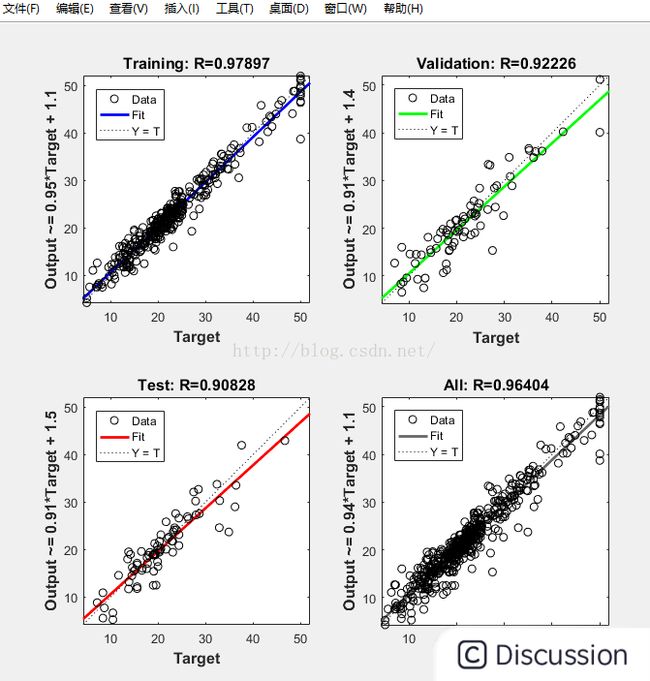 \ 最终的结果图
\ 最终的结果图
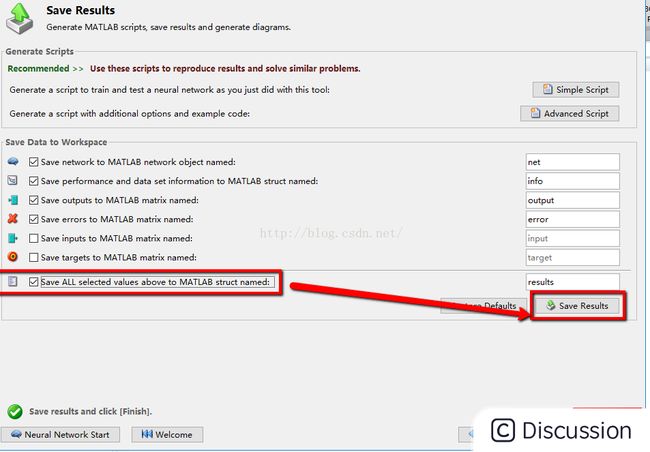
7:如果所得到的模型不能满足你的需求,则需重复上述的步骤直至能够得到你想要的精确度\ \ 8:将最终的得到的各种数据以及其拟合值进行保存,然后查看,就可以得到所要的拟合值\ \
\ \ 最后参考了网上和MATLAB的帮助,给出了一些与神经网络相关的函数,希望能够帮助大家。。\ 图形用户界面功能。 \ nnstart - 神经网络启动GUI \ nctool - 神经网络分类工具 \ nftool - 神经网络的拟合工具 \ nntraintool - 神经网络的训练工具 \ nprtool - 神经网络模式识别工具 \ ntstool - NFTool神经网络时间序列的工具 \ nntool - 神经网络工具箱的图形用户界面。 \ 查看 - 查看一个神经网络。 \ \ 网络的建立功能。 \ cascadeforwardnet - 串级,前馈神经网络。 \ competlayer - 竞争神经层。 \ distdelaynet - 分布时滞的神经网络。 \ elmannet - Elman神经网络。 \ feedforwardnet - 前馈神经网络。 \ fitnet - 函数拟合神经网络。 \ layrecnet - 分层递归神经网络。 \ linearlayer - 线性神经层。 \ lvqnet - 学习矢量量化(LVQ)神经网络。 \ narnet - 非线性自结合的时间序列网络。 \ narxnet - 非线性自结合的时间序列与外部输入网络。 \ newgrnn - 设计一个广义回归神经网络。 \ newhop - 建立经常性的Hopfield网络。 \ newlind - 设计一个线性层。 \ newpnn - 设计概率神经网络。 \ newrb - 径向基网络设计。 \ newrbe - 设计一个确切的径向基网络。 \ patternnet - 神经网络模式识别。 \ 感知 - 感知。 \ selforgmap - 自组织特征映射。 \ timedelaynet - 时滞神经网络。 \ \ 利用网络。 \ 网络 - 创建一个自定义神经网络。 \ SIM卡 - 模拟一个神经网络。 \ 初始化 - 初始化一个神经网络。 \ 适应 - 允许一个神经网络来适应。 \ 火车 - 火车的神经网络。 \ DISP键 - 显示一个神经网络的属性。 \ 显示 - 显示的名称和神经网络属性 \ adddelay - 添加延迟神经网络的反应。 \ closeloop - 神经网络的开放反馈转换到关闭反馈回路。 \ formwb - 表格偏见和成单个向量的权重。 \ getwb - 将它作为一个单一向量中的所有网络权值和偏差。 \ noloop - 删除神经网络的开放和关闭反馈回路。 \ 开环 - 转换神经网络反馈,打开封闭的反馈循环。 \ removedelay - 删除延迟神经网络的反应。 \ separatewb - 独立的偏见和重量/偏置向量的权重。 \ setwb - 将所有与单个矢量网络权值和偏差。 \ \ Simulink的支持。 \ gensim - 生成Simulink模块来模拟神经网络。 \ setsiminit - 集神经网络的Simulink模块的初始条件 \ getsiminit - 获取神经网络Simulink模块的初始条件 \ 神经元 - 神经网络Simulink的模块库。 \ \ 培训职能。 \ trainb - 批具有重量与偏见学习规则的培训。 \ trainbfg - 的BFGS拟牛顿倒传递。 \ trainbr - 贝叶斯规则的BP算法。 \ trainbu - 与重量与偏见一批无监督学习规则的培训。 \ trainbuwb - 与体重无监督学习规则与偏见一批培训。 \ trainc - 循环顺序重量/偏见的培训。 \ traincgb - 共轭鲍威尔比尔重新启动梯度反向传播。 \ traincgf - 共轭弗莱彻-里夫斯更新梯度反向传播。 \ traincgp - 共轭波拉克- Ribiere更新梯度反向传播。 \ traingd - 梯度下降反向传播。 \ traingda - 具有自适应LR的反向传播梯度下降。 \ traingdm - 与动量梯度下降。 \ traingdx - 梯度下降瓦特/惯性与自适应LR的反向传播。 \ trainlm - 采用Levenberg -马奎德倒传递。 \ trainoss - 一步割线倒传递。 \ trainr - 随机重量/偏见的培训。 \ trainrp - RPROP反向传播。 \ trainru - 无监督随机重量/偏见的培训。 \ 火车 - 顺序重量/偏见的培训。 \ trainscg - 规模化共轭梯度BP算法。 \ \ 绘图功能。 \ plotconfusion - 图分类混淆矩阵。 \ ploterrcorr - 误差自相关时间序列图。 \ ploterrhist - 绘制误差直方图。 \ plotfit - 绘图功能适合。 \ plotinerrcorr - 图输入错误的时间序列的互相关。 \ plotperform - 小区网络性能。 \ plotregression - 线性回归情节。 \ plotresponse - 动态网络图的时间序列响应。 \ plotroc - 绘制受试者工作特征。 \ plotsomhits - 小区自组织图来样打。 \ plotsomnc - 小区自组织映射邻居的连接。 \ plotsomnd - 小区自组织映射邻居的距离。 \ plotsomplanes - 小区自组织映射重量的飞机。 \ plotsompos - 小区自组织映射重量立场。 \ plotsomtop - 小区自组织映射的拓扑结构。 \ plottrainstate - 情节训练状态值。 \ plotwb - 图寒春重量和偏差值图。 \ \ 列出其他神经网络实现的功能。 \ nnadapt - 适应职能。 \ nnderivative - 衍生功能。 \ nndistance - 距离函数。 \ nndivision - 除功能。 \ nninitlayer - 初始化层功能。 \ nninitnetwork - 初始化网络功能。 \ nninitweight - 初始化权函数。 \ nnlearn - 学习功能。 \ nnnetinput - 净输入功能。 \ nnperformance - 性能的功能。 \ nnprocess - 处理功能。 \ nnsearch - 线搜索功能。 \ nntopology - 拓扑结构的功能。 \ nntransfer - 传递函数。 \ nnweight - 重量的功能。 \ nndemos - 神经网络工具箱的示威。 \ nndatasets - 神经网络工具箱的数据集。 \ nntextdemos - 神经网络设计教科书的示威。 \ nntextbook - 神经网络设计教科书的资讯。