因果推断学习笔记二

因果推断区别于传统的相关性研究很重要的一点是潜在结果框架, 也就是我们今天的topic所要涵盖的内容。今天的session我们将会cover以下几个话题：

1. 什么是潜在结果

2. 因果推断的核心问题

3. 对于核心问题的讨论和答案

4. 完整的实例

一、潜在结果

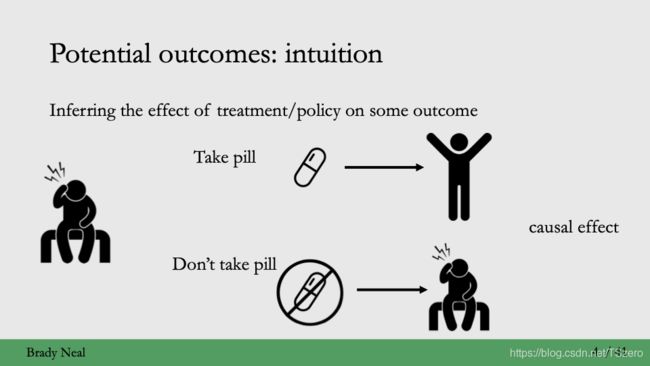
研究treatment对于结果的影响，我们想要同时知道同等条件下，不同treatment下的结果，从而能够得出结论，treatment的改变是否会导致结果的不同

例如
a) 吃药不吃药对于头痛个体(吃药前头痛)的影响

1. 不吃药头痛， 吃药之后不头痛：有因果效应
2. 不吃药不头痛，吃药后不头痛：没有因果效应

1.1 符号说明

我们先约定一下此次课程中所提到的符号，借助这些符号，把上面的因果效应的讨论抽象成数学公式。

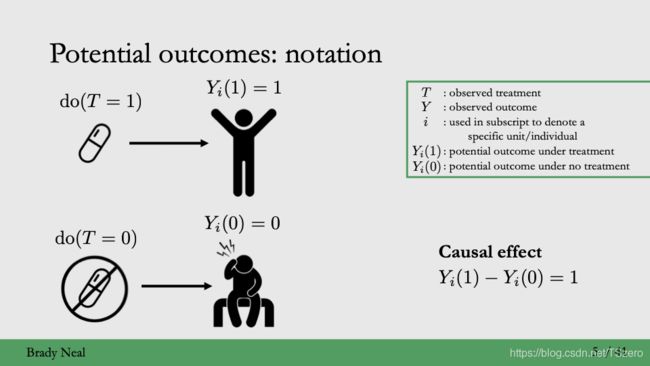
随机变量$X$表示$d$维的协变量(covariate)

$T$表示干预(treatment)
$Y$表示观测到的结果(observed outcome)，我们今天讨论的是二元treatment，也就是$T=0$或者$T=1$

$i$表示第$i$个样本(sample/unit/individual)

$Y_i(T)$表示对于样本$i$来说接受treatment T之后的潜在结果(potential outcome)，比如$Y_i(1),Y_i(0)$

$Y_i(1)-Y_i(0)$表示因果效应

1.2 因果推断的核心问题

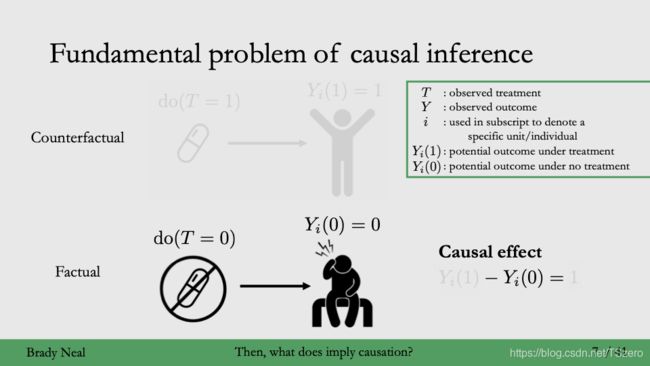
对于潜在结果，$\{Y_i(1),Y_i(0)\}$中只会有一个被观测到，因果效应ground truth缺失。实际观测到的结果，只可能是潜在结果中唯一的一个，被称为factual outcome，另一个观测不到的被称为counterfactual。例如前面的例子中提到的对于一个头痛个体，treatment只能二选一，而不能同时给予两个treatment，

      i.   吃药，factual是吃药的结果

      ii.  不吃药，factual是不吃药带来的结果

再举个例子：

滴滴向用户随机发送推荐短信(干预)，用户要么收到短信，要么收不到，这时候用户的反应，只能是其中一种情形下的结果，而不可能是两个结果。对于此短信的反应的实际结果只能依赖于二选一的干预，而不能看到干预和不干预下的用户分别的反应。


基于潜在结果模型，我们感兴趣的是平均因果效应(Average treatment effect，简记为ATE)

$$ATE:E[Y(1)-Y(0)]=E[Y(1)]–E[Y(0)]$$
在大数据时代和统计学中经典的大数定律，使我们能够利用大样本平均来估计平均因果效应。

但与此同时，如下图表格中所示，对于每个样本来说，$Y(1)$和$Y(0)$是潜在结果，$Y(1)-Y(0)$没有真实的值，分布未可知，无法用统计学方法去估计。

而对于$E[Y(1)]$和$E[Y(0)]$，$Y_i(1)$是潜在结果，它们之间并不是独立同分布的，没有任何假设，利用大样本直接求平均来估计$E[Y(1)]$是不对的（大数定律要求数据是独立同分布的）。

因此为了估计左边的$ATE,$ 需要把它转换成右边随机变量$Y$关于$T$的分布, 给定$T$，也就是右边的$Y$和$T$之间的相关性模型，从而在随机变量$(X,T,Y)$上我们能够定义分布的，可以用大数定律或者统计模型求解。

因此核心在于通过设置合理的假设，在$E[Y(1)]-E[Y(0)]=E[Y|T=1]–E[Y|T=0]$左右两边建立等号，也就是接下来我们课程的重点讨论对象。

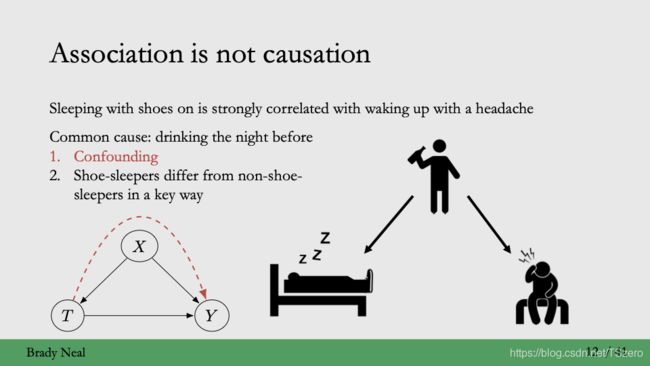
通过上面的讨论，我们了解到，潜在结果决定了相关性关系(右边)并不等价于因果关系(左边)

举个通俗的例子：穿鞋子睡觉和起床头疼有强相关关系，但是不一定会有因果关系，可能真正的原因比如，前一天晚上喝酒，这种情况下喝酒就是混淆变量(confounding)，也就是既会影响treatment，又会影响结果； 再比如，穿鞋子和不穿鞋子的人群不一样，有显著的差别，这两组接受穿鞋子treatment的人群是不可比的(non-overlapping)，比如穿鞋子睡觉的绝大多数可能都是喝醉的人，而不穿鞋子睡觉中绝大多数都是清醒的人，从而两个人群是不一致的。可比的人群应该是：穿鞋子和不穿鞋子的人群里面的喝酒的人以及清醒的人分布是一致的

再举个例子：冰激凌涨价和雪山融化有相关关系，但没有因果关系，冰激凌涨价不会引起雪山融化，但是他们都通过天气变热联系起来。天气变热导致冰激凌涨价(影响treatment)，同时也会导致雪山融化(影响结果)，它就是一个混淆变量。

1.3 两个假设

1.3.1 Ignorability假设

为了从因果性模型转换到相关性模型，从confounding出发，我们考虑如下三个等价的假设

1. Ignorability
2. exchangability
3. unconfoundedness

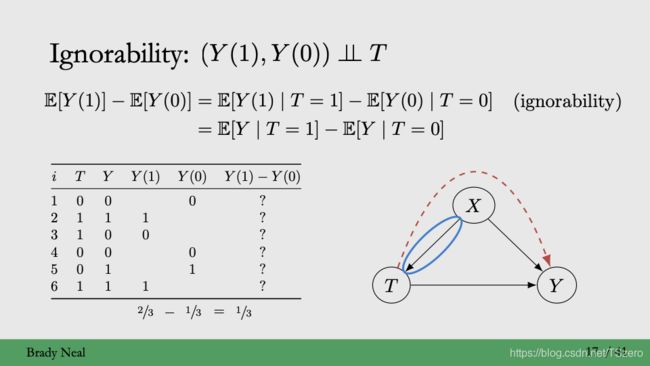
Ignorability名字的由来是加了这个假设之后，潜在结果中的question Marks可以直接忽略，或者说counterfactual outcome可以忽略，从而能够取实际的观测结果来估计。严格来说，Ignorability指潜在结果与实际的treatment的分配无关，如果有confounding的话，即既会影响treatment，又会影响结果，就比如在如下的因果图中所示，潜在结果会和treatment之间有额外的confounding的通道，从而潜在结果和treatment不能保持独立。因此ignorability保证了unconfoundedness。，即没有混淆变量的影响

Exchangeability: 接受treatment和不接受treatment的组别之间是可以交换的

$E[Y(1)]-E[Y(0)]$

$=P(T=1)E[Y(1)|T=1]+P(T=0)E[Y(1)|T=0]-(P(T=0)E[Y(0)|T=0]+P(T=1)E[Y(0)|T=1])$

$=(P(T=1)+P(T=0))\times E[Y(1)|T=1]–(P(T=1)+P(T=0))\times E[Y(0)|T=0]$

$=E[Y(1)|T=1]-E[Y(0)|T=0]$

上述的推导证明了Ignorability 和exchangability 这两种说法是等价的，都能够通过去除confounding来去除掉treatment对于潜在的结果的影响。

1.3.2 consistency假设

除了ignorability, 我们还需要假设：consistency

1. 接受的treatment唯一确定结果
2. T = t 代表观测到的Y就是基于t的潜在结果

Along with consistency, 我们还需要额外的假设

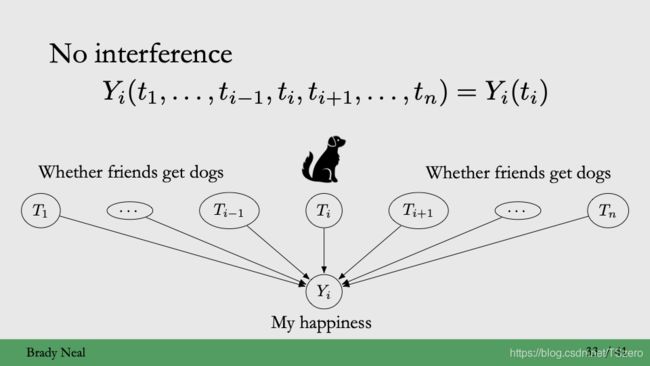
1. 没有干扰(No interference)
2. 对于第i个样本来说，ta自己的treatment唯一的确定了结果，别的样本的treatment对于其最终的结果没有影响，比如在如下狗狗的例子中，我是否快乐其实只与我自己的treatment(自己有狗狗)有关，而与别的treatment(朋友有没有狗狗)无关，样本i不受其他的treatment的干扰。

综合以上ignorability, consistency, no interference假设，我们可以得到ATE的调整公式：

$E[Y(1)]-E[Y(0)]$ (no interference)

$=E[Y(1)|T=1]-E[Y(0)|T=0]$ (Ignorability)

$=E[Y|T=1]-E[Y|T=0]$ (consistenty)
 

一个很自然的问题是，是不是这两个假设总能成立？答案是it depends。

首先我们先讨论ignorability。对于Randomized Control Trial(RCT)， 比如通过抛硬币来决定随机给予treatment(穿鞋子睡觉，不穿鞋子睡觉)，这个假设就是成立的，没有混淆变量喝酒，喝酒和清醒的人在treatment间没有差异，潜在结果和treatment独立。

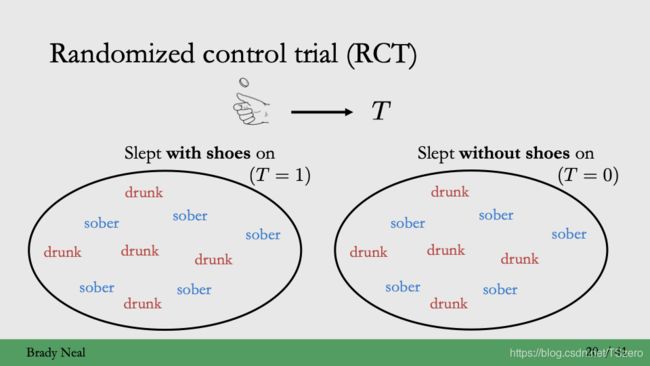
那么什么时候这个假设不成立呢？

举个例子：在滴滴，通过日志拿到的数据是观测数据，用户接受的treatment已经是通过乘客模型和策略调节过的，已经不再满足ignorability。
 
 

接下来我们讨论consistency的假设，它也不总是成立。

举个例子：$T=1$代表有狗狗，那么只要有狗狗，最终个体的结果Y就是基于有狗狗的结果——快乐, 而与狗狗的品类无关。如下图所示，就是一个不满足consistency的例子，最终的结果不只取决于实际接受的treatment，还可能收到别的干扰。

再来一个例子：在滴滴，比如给司机补贴，司机会决定接不接单，这个结果不只取决于给司机本人的treatment，还可能会受到司机周围的司机所受到的补贴的影响，这个时候consistency就不能得到满足。

ignorability和consistency，no interference使我们能够在$ATE$的左右两端建立等号，也就能够通过统计学的方法去估计因果效应，这个过程被称作identifiation。如果一个因果目标，可以通过统计分布估计得到，这个因果quantity就是可识别的(identifiable)，比如ate，以及接下来我们更感兴趣的cate。添加假设建立等式的过程就是identification。

identification：从因果量到统计量，把个体效应的因果模型转换到可估计的相关性模型

二、CATE

通常情况下，考虑异质性的因果效应可以给我们更多的信息，能够从协变量(individual)层面更加细致的区分因果效应, heterogeneous treatment effect(hte)，conditional average treatment effect (cate) 或者等价的 individual treatment effect(ite)

• 定义 E[Y(1)-Y(0)|X]

• identification

  $E[Y(1)-Y(0)|X]$(no interference)

  ? $=E[Y(1)|T=1,X]–E[Y(0)|T=0,X]$ (？假设)

  ? $=E[Y|T=1,X]-E[Y|T=0,X]$(consistency)

2.1 两个假设

2.1.1 conditional ignorability

核心假设：等价的假设

• conditional ignorability
• conditional exchangeability
• unfoundedness

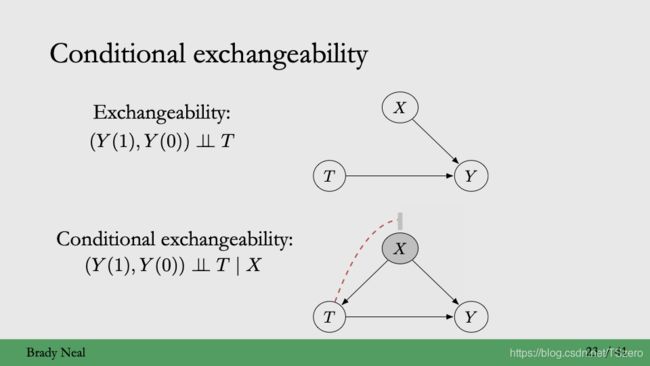
这里的conditional ignorability指的是给定协变量covariate，潜在结果与treatment无关，也就是基于covariate的条件独立，反映在因果图上就是切断给定协变量，outcome和treatment之间由于潜在的confounding而可能存在的的联系。引入conditional ignorability或者conditional exchangability的原因在于，unconfoundedness是没有办法实际中验证的，因为我们不知道是否有未观测到的confounding，而这些很可能会在treatment和outcome之间建立别的通道。

2.1.2 Positivity

不同于$ATE$, $CATE$的估计还需要额外的假设：正定性(Positivity)

正定性(Positivity)定义：

离散treatment: 概率$P(T|X)>0$， 给定协变量之后任意treatment的概率都严格大于0，
也就是通常所说的倾向性评分(propensity score)严格大于0

连续treatment: 更严格的要求generalized propensity score概率密度$p(T|X)>0$

1. Mathematical formulation（数学公式）

从$CATE$的计算公式出发，可以得到propensity score是作为分母中的一项，若为0，则该计算表达式无定义，从而无法计算得到cate或者ate

2. 直观解释：Overlap

Positivity保证了$T=1$和$T=0$的人群是完全重合的。如果有positivity violation(违反)的话，比如说关于第一维协变量人群有50%的重合，这样子随着协变量维数d的增加，重合的部分会逐渐的减小，衰减直至人群几乎无重合$(0.5{)}^d～0$，也就是通常所说的维数灾难(curse of dimensionality)

3. 外推能力：

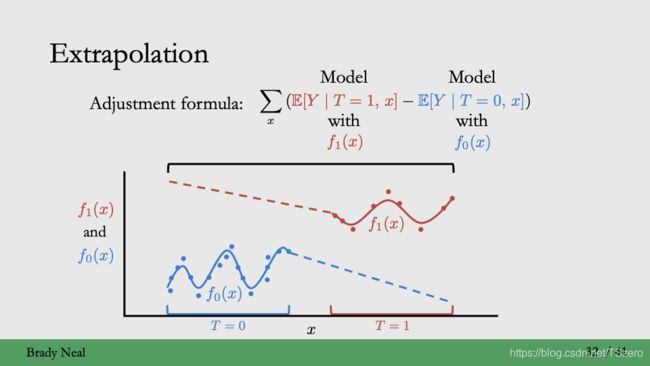
Positivity violation会带来模型外推能力的变差

如下图所示，在identification之后得到的统计估计中，$T=1$建模得到的模型不能迁移到另一个$T=0$，因为数据之间的gap，因此计算得到cate可能是有偏差的

still，有没有不满足positivity的情形呢？

举个例子：

在滴滴，定价策略基础调节，基于城市粒度调节，对于城市的所有人，treatment都是调价，没有不调价的，那么P(T=1|X) = 1, P(T=0|X) = 0, positivy就不满足

2.2 causal quantity和statistical quantity之间的等式

有了这两个假设，就能够如下图所示，建立causal quantity和statistical quantity之间的等式

• cate identification
• by-product: 得到基于个体水平的因果效应$CATE$之后，依据双期望定理(条件期望的期望是无条件期望)，我们依旧可以得到$ATE$，也就是总体水平的因果效应

2.3 总结

2.3.1 假设

因为潜在结果，因果模型推断估计CATE/ATE所需要的假设

• Conditional Ignorability / Ignorability
• Positivity/NA
• Consistency/Consistency
• No interference/No interference

2.3.2 依赖的数学定理

• Linearity of expectation（期望的线形性质）
• The overall expectation can be computed by taking expectation on conditional expectation（重期望定理）
  
  

更加general的统计学名词clarification

Estimand是任何想要去估计的量
Estimate是基于数据的统计量，可作为estimand的估计
Estimation指的是从得到数据，得到统计量去估计estimand的过程

Potential outcome framework决定了causal estimand是不能直接估计的。本次session讨论的以上假设都是在把一个causal estimand转化成一个统计学的estimand，从而可以利用统计学的estimation获取得到相应的estimate，也就是如下所示的identification-estimation flowchart。如何去做有效的estimation，比如减小方差和减小bias，提高模型准确度，是因果推断中的另一重点和算法聚焦。

三、实例

基于potential outcome framework，我们以下面的一个因果推断的实例，展示一个从identification到用estimation来估计$ATE$的链路。

3.1背景

46%的美国人有高血压，高血压和死亡率的增加相关，因此想要研究钠的摄入对于高血压的影响(effect)。

数据主要的notation为:

Y: 血压;
T: 钠的摄入;
X: 年龄和流失的蛋白质。

3.2 估计

Causal Estimand: ATE = E[Y(1)-Y(0)]

Identifiacation: 该实例是仿真数据集，满足conditional ignorability,positivity; consistency, 同时真实的ATE已知，我们可以从中检验模型的准确度

Estimation:

1. outcome对于样本关于treatment和covariate进行线性回归, 得到cate的相关性模型； Ate的计算通过对cate按照样本的分布来估计，通常假设样本是i.i.d.分布的，从而可以通过大数定律来得到ate的估计值(直接取平均得到), 计算得到的ate和真实的ate差别较小
2. 另一种可能的办法：直接outcome关于treatment回归，计算得到ate，但这种方法计算得到的ate和真实值的mape误差很大
3. 从而验证了在因果模型中加入异质性的重要性，也就是如上讨论cate的估计。

$Y=aT+bX$
$Y=aT$

3.3 思考以及展望:

以上具体实例中，estimation采用线性回归的相关性模型，会有一些缺陷，比如说对于所有的个体而言，他们的因果效应都是线性模型中treatmentT的斜率，a是一样的，在很多时候是不符合常理的，不能区分异质水平上的因果效应。更加advanced的拓展方法可参考：

最后，我们在本节课程中主要讨论了二元treatment下的潜在因果，潜在因果模型的框架需要identification，同时也为后面的statistical estimation提供了不一样的评价体系，比如qini score，区别于传统统计学习的mse。更重要的是，同样的逻辑可以轻松的拓展到多元treatment潜在结果模型和连续treatment潜在结果模型，通过添加合理(更强)的假设，也可以完成identification，转换到statistical estimation，通过更加复杂的算法来得到相应的estimate。