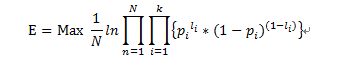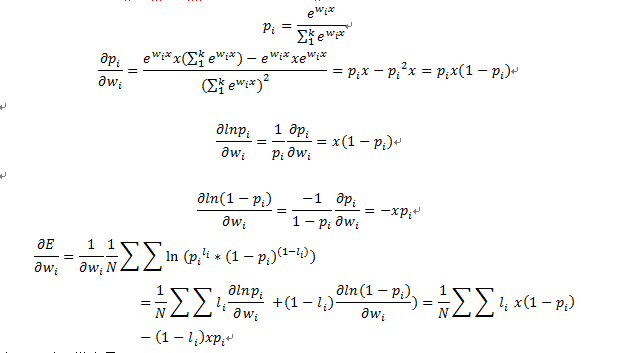原理
语言模型用来在给定上下文的前提下预测下一个词出现概率。具体的讲就是,在给定词组 wi wi+1 … wn-1的情况下,预测下一个词是wn的概率,即p(wn|wi wi+1 … wn-1)。传统的语言模型训练采用最大似然的方法训练参数,例如
P(wn| wi wi+1 … wn-1) = Count(wi wi+1 … wn-1 wn)/Count(wi wi+1 … wn-1).
这种训练方法简单直观但是缺点也非常明显,对于三元组
p(wi|wi-2 wi-1)=Count(wi-2 wi-1 wi)/Count(wi-2 wi-1)
如果词汇表的大小为N,那么必须要预测N^3个参数,需要预测的参数太多,会有大量的三元组从未在训练语料中出现。为了解决上述的数据稀疏问题,各种平滑算法应运而生,最简单的就是加一平滑算法。目前效果最好的是Modified KN平滑算法。但是平滑算法从理论上并不能完美的证明其正确性,在实际训练过程中需要添加较多的trick,并且传统语言模型的可扩展性不高,高阶的语言模型很难用最大似然的方法训练。
而用神经网络训练语言模型可以很好的解决上述问题。我们采用四层神经网络构建语言模型,如图所示:
假设一个训练实例w1w2w3w4, 也就是求p(w4|w1w2w3)。首先查找w1,w2,w3词的词向量,设词向量的长度为dim,并将三个词的向量按照顺序首位拼接成大的向量(3*dim)作为隐藏层1的输入向量。
设隐藏层1有n个结点,每个结点用一个向量表示,这个向量的长度是3*dim, 用输入向量和输入层的每一个结点的向量做点乘,作为结点的初始输出。再对每一个结点的输出结果做一个“激活”,这就是所谓的激活函数。输入层每个结点的结果再经过激活函数,输出结果是长度为n的向量,将这个向量作为隐藏层2的输入向量。
隐藏层2有outdim个结点,每个结点用一个长度为n的向量表示,同理,将隐藏层2的输入的向量和其每一个结点点乘,对结果进行激活之后,就是隐藏层2的输出向量,作为输出层的输入向量传入输出层。
设有k个词,那么输出层有k个结点,每个结点用一个长度为outdim的向量表示。在输出层用输入向量与每个结点点乘,最后对每个结点进行softmax, ,si是经过softmax之后的输出层的输出向量的分量,pi可以理解为预测w1 w2 w3后面是wi的概率。输出层在经过softmax之后,结果就是一个长度为k的向量,这个向量的大部分分量的值等于或者接近0,其中一个分量的值等于或者接近1。设共有10个词,那么w4就可以表示为L4=[0,0,0,1,0,0,0,0,0,0],我们希望w1w2w3在经过神经网络计算之后的输出的向量和w4的向量比较接近,越接近说明模型计算的越准。
设一共有N个训练实例,目标函数可以写为:
Pi可以看做是输出向量在i分量上的标签为1的概率,1-pi就可以看做是在i分量上的标签为0的概率,li是输出层的正确输出向量的分量,。最大化E就是让神经网络的输出层的结果和正确结果的匹配程度越大,即让标签为1的分量的概率越大,让标签为0的分量的概率越小。
输出层的初始结果si = wi*x, wi表示输出层结点i的向量。
当li=1时,梯度是x(1-pi)
当li=0时,梯度是-xpi=x(0-pi)
可以总结为x(li-pi)
li作为正确标注,pi是系统的实际输出,那么梯度就是 “错误*x”,这也符合我们对参数更新的一般印象,就是通过系统输出的错误调整参数。
分布式训练
神经网络训练速度很慢,主要的瓶颈在于大矩阵相乘。有两种解决方案,一是分布式训练,让每台机器训练的数据减少,进而减少整体数据的训练时间;二是优化矩阵相乘,相比第一种方法减少通信代价。
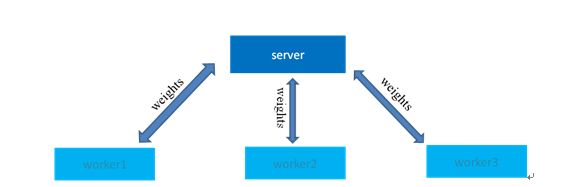
为了获得较高的训练速度,我们采用异步的分布式训练架构。首先将训练数据按照worker数量进行划分,每个worker负责各自的数据片,worker按照一定的频率异步的和server交换训练的参数。参考平均感知机(一层的神经网络)的训练方法,server端每收到任一worker的参数,就和本身的参数做一次平均,将这次平均的结果作为最新的参数,并发送给这个worker,worker收到新的参数之后,就在新参数上继续训练。
分布式训练可以显著的提高训练速度,并且模型效果也不会有明显的下降,但是由于训练过程中多台机器涉及到大量的数据通信,系统稳定性受到较大影响。
GPU
加速训练的另一个思路是运算操作的加速。目前通常使用intel出品的MKL数学函数库和多线程技术实现运算的加速,但是限于CPU运算的核数和浮点数运算速度,目前的速度还是不能较为快速的训练模型。
一般用于计算平台的GPU通常拥有两千多个计算核,每秒浮点数运算次数是普通CPU的几百倍, CUDA是基于GPU的并行运算平台,并提供了多种应用开发库。通过上文的公式可以看出,神经网络模型在训练过程中的大部分操作都可以用矩阵运算表示,输入层和输出层可以用稀疏矩阵相乘表示,隐藏层用密集矩阵相乘表示,分别对应CUSPARSE和CUBLAS库。对于隐藏层的运算可以直接调用CUBLAS库进行运算,而对于输入输出层的稀疏矩阵运算,将数据格式转换为CUSPARSE需要的格式所花费的时间远远大于调用稀疏矩阵函数的时间。对于这种情况,我们采用直接编写kernel函数的方法解决。对于输入层的前向传播操作,直接的写法是:
而GPU的kernel函数是:
仅从函数分析时间复杂度,可以看出,从O(n^3)降低为O(1)。但是实际上GPU要处理内存寄存器的加载,线程的协调等,耗时的上限是O(n^3)/2496,其中2496是我们所用nvidia tesla k20 GPU的核数。
相比GPU的计算能力,对显存的分配,以及内存拷贝到显存,这两种操作的时间消耗非常大,所以程序只是在开始的时候先分配好显存,内存和显存之间的相互拷贝在训练过程中也要尽可能的少。显存相比内存要小很多,k20的显存只有5G,我们采用两级拷贝的策略,减少训练过程中的IO操作。先从硬盘上加载较多的训练数据,在训练过程中,再从内存中批量拷贝到显存。
运行同样的数据,基于MKL的程序,一轮需要35000秒到45000秒之间,GPU需要7000秒左右,从总时间上看,GPU比MKL快了5到6倍。
在训练10轮的情况下,GPU耗时19个小时,比分布式的训练方法快了4个小时。
实验结果
•训练数据:10623066句,250422725五元实例
•训练语料130623066句,20亿的4元实例
总结
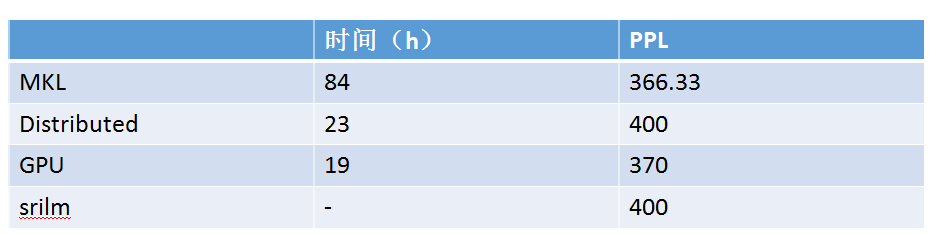
在神经网络模型不调优的情况下,千万级别数据训练出来的模型优于ngram语言模型,但是在10亿级别数据下,神经网络模型要差于ngram模型。Ngram模型可以理解为是一个规则系统,每个词组都对应一个概率,如果我们的训练语料非常大,从理论上讲可以统计出几乎所有词组的概率,那么计算词组的概率就可以看做是一个查表的过程。神经网络语言对于出现过的词组和没出现过的词组都是通过计算得出的,如果测试语料有限,那么ngram语言模型可能表现会更好。
神经网络或者深度学习在图像和语言领域都取得了突破性的进展,在自然语言处理领域应用神经网络模型还处于探索阶段,神经网络的潜力还需要进一步的挖掘。