pytorch learn 05 多层神经网络,Sequential 和 Module
From: https://github.com/L1aoXingyu/code-of-learn-deep-learning-with-pytorch
在前面的线性回归中,我们的公式是 y = w x + b y = w x + b y=wx+b,而在 Logistic 回归中,我们的公式是 y = S i g m o i d ( w x + b ) y = Sigmoid(w x + b) y=Sigmoid(wx+b),其实它们都可以看成单层神经网络,其中 Sigmoid 被称为激活函数。
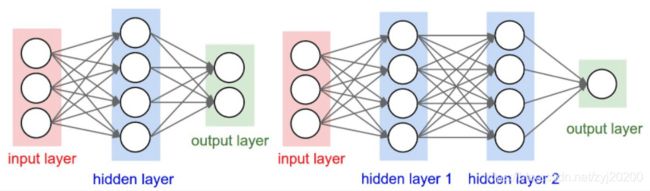
神经网络就是很多个神经元堆在一起形成一层神经网络,那么多个层堆叠在一起就是深层神经网络,我们可以通过下面的图展示一个两层的神经网络和三层的神经网络。
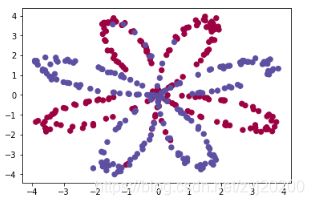
数据
m = 400 # 样本数
N = int(m/2) # 每类样本数
D = 2 # 维度
x = np.zeros((m, D))
y = np.zeros((m, 1), dtype='uint8')
a = 4
for j in range(2):
ix = range(N*j, N*(j+1))
t = np.linspace(j*3.12, (j+1)*3.12, N) + np.random.randn(N)*0.2 # theta
r = a * np.sin(4*t) + np.random.randn(N)*0.2
x[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
y[ix] = j
plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)
使用logistic进行训练
x_train = torch.from_numpy(x).float()
y_train = torch.from_numpy(y).float()
w = nn.Parameter(torch.randn(2, 1))
b = nn.Parameter(torch.zeros(1))
optimizer = torch.optim.SGD([w, b], 1e-1)
def logistic_regression(x):
return torch.mm(x, w) + b
criterion = nn.BCEWithLogitsLoss()
for i in range(100):
out = logistic_regression(Variable(x_train))
loss = criterion(out, Variable(y_train))
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (1+i) % 20 == 0:
print('epoch: {}, loss: {}'.format(i+1, loss.data.numpy()))
def plot_logistic(x):
x = Variable(torch.from_numpy(x).float())
out = F.sigmoid(logistic_regression(x))
out = (out > 0.5) * 1
return out.data.numpy()
plot_decision_boundary(lambda x_train: plot_logistic(x_train), x_train.numpy(), y_train.numpy())
plt.title('logistic regression')
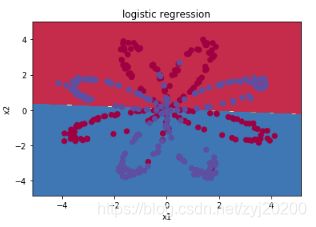
可以看到,logistic 回归并不能很好的区分开这个复杂的数据集,如果你还记得前面的内容,你就知道 logistic 回归是一个线性分类器,这个时候就该我们的神经网络登场了!
neural network
w1 = nn.Parameter(torch.randn(2, 4)*0.01)
b1 = nn.Parameter(torch.zeros(4))
w2 = nn.Parameter(torch.randn(4, 1)*0.01)
b2 = nn.Parameter(torch.zeros(1))
def two_network(x):
x1 = torch.mm(x, w1) + b1
x1 = F.tanh(x1)
x2 = torch.mm(x1, w2) + b2
return x2
optimizer = torch.optim.SGD([w1, w2, b1, b2], 1.0)
criterion = nn.BCEWithLogitsLoss()
for i in range(1000):
out = two_network(Variable(x_train))
loss = criterion(out, Variable(y_train))
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1) % 200 == 0:
print('epoch: {}, loss: {}'.format(i+1, loss.data.numpy()))
def plot_network(x):
x = Variable(torch.from_numpy(x).float())
x1 = torch.mm(x, w1) + b1
x1 = F.tanh(x1)
x2 = torch.mm(x1, w2) + b2
out = F.sigmoid(x2)
out = (out > 0.5) * 1
return out.data.numpy()
plot_decision_boundary(lambda x_train: plot_network(x_train), x_train.numpy(), y_train.numpy())
plt.title('2 layer network')
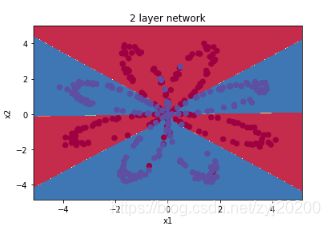
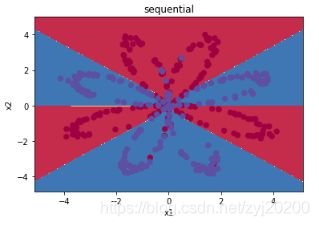
可以看到神经网络能够非常好地分类这个复杂的数据,和前面的 logistic 回归相比,神经网络因为有了激活函数的存在,成了一个非线性分类器,所以神经网络分类的边界更加复杂。
Sequential 和 Module
Sequential 允许我们构建序列化的模块,而 Module 是一种更加灵活的模型定义方式
Sequential
seq_net = nn.Sequential(
nn.Linear(2, 4),
nn.Tanh(),
nn.Linear(4, 1)
)
params = seq_net.parameters()
optim = torch.optim.SGD(params, 1.0)
criterion = nn.BCEWithLogitsLoss()
for i in range(1000):
out = seq_net(Variable(x_train))
loss = criterion(out, Variable(y_train))
optim.zero_grad()
loss.backward()
optim.step()
if (i+1)%200 == 0:
print('epoch: {}, loss: {}'.format(i+1, loss.data.numpy()))
def plot_seq(x):
out = F.sigmoid(seq_net(Variable(torch.from_numpy(x).float()))).data.numpy()
out = (out > 0.5) * 1
return out
plot_decision_boundary(lambda x_train: plot_seq(x_train), x_train.numpy(), y_train.numpy())
plt.title('sequential')
Module
模板
class 网络名字(nn.Module):
def __init__(self, 一些定义的参数):
super(网络名字, self).__init__()
self.layer1 = nn.Linear(num_input, num_hidden)
self.layer2 = nn.Sequential(...)
...
定义需要用的网络层
def forward(self, x): # 定义前向传播
x1 = self.layer1(x)
x2 = self.layer2(x)
x = x1 + x2
...
return x
class module_net(nn.Module):
def __init__(self, num_input, num_hidden, num_output):
super(module_net, self).__init__()
self.layer1 = nn.Linear(num_input, num_hidden)
self.layer2 = nn.Tanh()
self.layer3 = nn.Linear(num_hidden, num_output)
def forward(self, x):
x1 = self.layer1(x)
x2 = self.layer2(x1)
x3 = self.layer3(x2)
return x3
mo_net = module_net(2, 4, 1)
optimizer = torch.optim.SGD(mo_net.parameters(), 1.0)
criterion = nn.BCEWithLogitsLoss()
for i in range(1000):
out = mo_net(Variable(x_train))
loss = criterion(out, Variable(y_train))
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1)%200 == 0:
print('epoch: {}, loss: {}'.format(i+1, loss.data.numpy()))
epoch: 200, loss: 0.2764633595943451
epoch: 400, loss: 0.2612650990486145
epoch: 600, loss: 0.24757547676563263
epoch: 800, loss: 0.2373933643102646
epoch: 1000, loss: 0.2298329472541809
模型存储&加载
Sequential 存储参数和模型结构
torch.save(seq_net, 'module/sample_seq_net.pth')
seq_net1 = torch.load('module/sample_seq_net.pth')
Sequential 存储模型参数
如果要重新读入模型的参数,首先我们需要重新定义一次模型,接着重新读入参数
torch.save(seq_net.state_dict(), 'module/sample_seq_net_params.pth')
seq_net2 = nn.Sequential(
nn.Linear(2, 4),
nn.Tanh(),
nn.Linear(4, 1)
)
seq_net2.load_state_dict(torch.load('module/sample_seq_net_params.pth'))
Module 模型存储加载
# 模型存储
torch.save(mo_net, 'module/module_net.pth')
# 加载模型
mo_net2 = torch.load('module/module_net.pth')