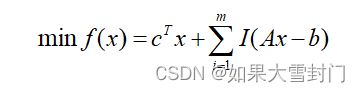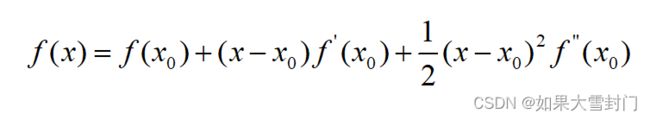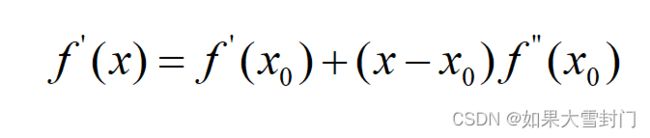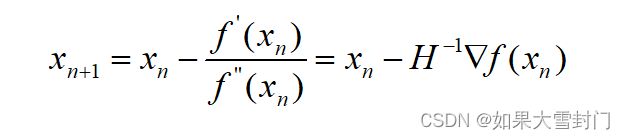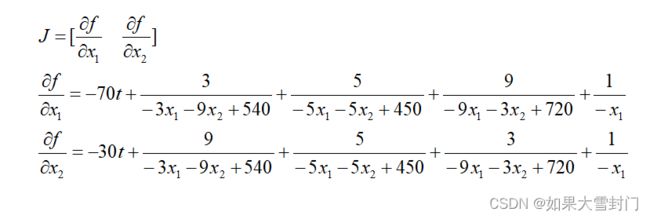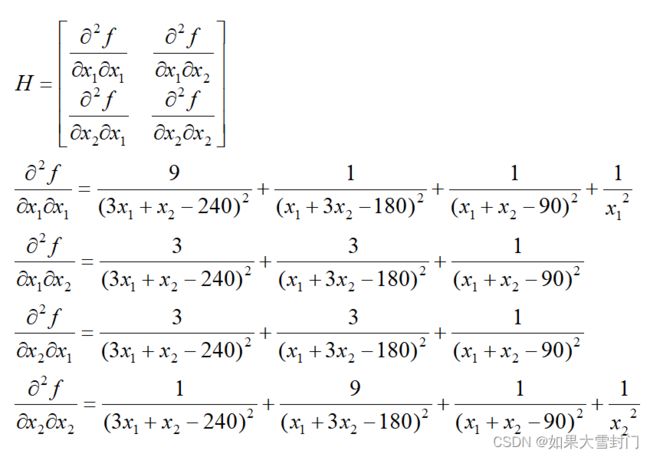python最优化算法实战---线性规划之内点法
1.内点法概述
内点法是求解线性规划的一个方法,是求解不等式约束最优化问题的一种十分有效的方法,但不能处理等式约束。内点法在大规模线性优化,二次优化,非线性规划方面都有比较好的表现,内点法是多项式算法,随着问题规模的增大,计算的复杂度却不会急剧增大。
本文主要介绍使用障碍函数思想的内点法,该思想的内点法的主要思想是在可行域的边界筑起一道很高的"围墙",当迭代点靠近边界时,目标函数陡然增大,以示惩罚,阻止迭代点穿越边界,这样就可以将最优解挡在可行域的范围之内了。此类内点法的求解思路同拉格朗日松弛法类似,将约束问题转化为无约束问题,通过无约束函数的梯度下降进行迭代直至得到最优解。
2.内点法过程
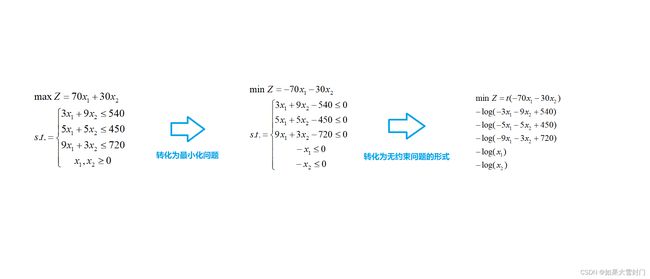
内点法第一步便是将约束问题转换为非约束问题,对于一个最小化线性规划问题,如下图所示
借鉴拉格朗么松弛法的思路,这个线性规划问题可以表示成如下函数 。
其中m是约束方程的个数,I是指示函数,一般定义如下:
通过指示函数可以将约束方程直接写到目标函数中,然后对目标函数求极小值。但是这个指示函数I(u)是不可导的,通常用如下的函数替代:
由于指数函数I_(u)是凸函数,所以新的目标函数也是凸函数,因此可以用凸优化中的方法来求解该函数的最小值,下文将使用经典的牛顿法讲解如何求函数最小化问题。
目标函数f(x)在x0做二阶泰勒公式展开得到
针对上述等式继续进行运算, 上面等式两边同时对(x-x0)求导,并令导数为0,得到如下结果
继续对上述等式进行变换,可以得到
这样就得到了下一点的位置,,从x0走到x1。重复这个过程,直到到达导数为0的点,由此可以得到达牛顿法的迭代公式如下
其中H^-1表示二阶导数矩阵(海塞矩阵)的逆,所以如果使用牛顿法求解目标函数的最优值,需要知道目标函数的一阶导数和二阶导数。
在问题中目标函数一阶导数和二阶导数分别如下:
3.内点法代码
可以使用python符号计算库sympy计算目标函数的一阶导数和二阶导数,计算出相应的表达式,其结果如代码中所示。
"""
内点法
python库sympy中集成了许多用于计算一阶导数和二阶导数的函数
"""
from sympy import diff,symbols,exp,log
# 定义变量
x1,x2,t = symbols('x1 x2 t')
# 定义目标函数
func = t*(-70*x1-30*x2)-log(-3*x1-9*x2+540)-log(-5*x1-5*x2+450)-log(-9*x1-3*x2+720)-log(x1)-log(x2)
# 求导
de_x1 = diff(func,x1,1) # 对x1求一阶导
de_x2 = diff(func,x2,1) # 对x2求一阶导
de_x1_x1 = diff(func,x1,x1) # 对x1和x1求二阶导
de_x1_x2 = diff(func,x1,x2) # 对x1和x2求二阶导
de_x2_x1 = diff(func,x2,x1) # 对x2和x1求二阶导
de_x2_x2 = diff(func,x2,x2) # 对x2和x2求二阶导
"""
得到的结果:
de_x1 = -70*t + 3/(-3*x1 - 9*x2 + 540) + 5/(-5*x1 - 5*x2 + 450) + 9/(-9*x1 - 3*x2 + 720) - 1/x1
de_x2 = -30*t + 9/(-3*x1 - 9*x2 + 540) + 5/(-5*x1 - 5*x2 + 450) + 3/(-9*x1 - 3*x2 + 720) - 1/x2
de_x1_x1 = 9/(3*x1 + x2 - 240)**2 + (x1 + 3*x2 - 180)**(-2) + (x1 + x2 - 90)**(-2) + x1**(-2)
de_x1_x2 = 3/(3*x1 + x2 - 240)**2 + 3/(x1 + 3*x2 - 180)**2 + (x1 + x2 - 90)**(-2)
de_x2_x1 = 3/(3*x1 + x2 - 240)**2 + 3/(x1 + 3*x2 - 180)**2 + (x1 + x2 - 90)**(-2)
de_x2_x2 = (3*x1 + x2 - 240)**(-2) + 9/(x1 + 3*x2 - 180)**2 + (x1 + x2 - 90)**(-2) + x2**(-2)
"""牛顿迭代过程代码
"""
内点法实现代码
"""
import numpy as np
# 计算目标函数在x处的一阶导数
def gradient(x1, x2, t):
j1 = -70*t + 3/(-3*x1 - 9*x2 + 540) + 5/(-5*x1 - 5*x2 + 450) + 9/(-9*x1 - 3*x2 + 720) - 1/x1
j2 = -30*t + 9/(-3*x1 - 9*x2 + 540) + 5/(-5*x1 - 5*x2 + 450) + 3/(-9*x1 - 3*x2 + 720) - 1/x2
return np.asmatrix([j1, j2]).T
# 求二阶导数矩阵(海塞矩阵)的逆矩阵
def inv_hessian(x1, x2):
x1, x2 = float(x1), float(x2)
h11 = 9/(3*x1 + x2 - 240)**2 + (x1 + 3*x2 - 180)**(-2) + (x1 + x2 - 90)**(-2) + x1**(-2)
h12 = 3/(3*x1 + x2 - 240)**2 + 3/(x1 + 3*x2 - 180)**2 + (x1 + x2 - 90)**(-2)
h21 = 3/(3*x1 + x2 - 240)**2 + 3/(x1 + 3*x2 - 180)**2 + (x1 + x2 - 90)**(-2)
h22 = (3*x1 + x2 - 240)**(-2) + 9/(x1 + 3*x2 - 180)**2 + (x1 + x2 - 90)**(-2) + x2**(-2)
H = np.asmatrix([[h11,h12],[h21,h22]])
H_1 = np.linalg.inv(H)
return H_1
# 明确目标函数
x = np.array([[10], [10]]) # x是牛顿法的初始迭代值
t = 0.00001 # t是值函数中的t
# 迭代停止的控制条件
eps = 0.01 # 迭代停止的误差
iter_cnt = 0 # 记录迭代的次数
while iter_cnt < 20:
iter_cnt += 1
J = gradient(x[0,0], x[1,0], t)
H_1 = inv_hessian(x[0,0], x[1,0])
x_new = x - H_1*J # 牛顿法公式
error = np.linalg.norm(x_new - x) # 求二范数,判断迭代效果
print('迭代次数是:%d, x1=%.2f, x2=%.2f, 误差是:%.2f'%(iter_cnt,x_new[0,0],x_new[1,0],error))
x = x_new
if error < eps:
break
# 输出最终结果
print("目标函数的值是:%.2f"%float(70*x[0,0]+30*x[1,0]))
"""
最终的运行结果:
迭代次数是:1, x1=15.91, x2=15.34, 误差是:7.96
迭代次数是:2, x1=20.13, x2=18.19, 误差是:5.09
迭代次数是:3, x1=21.00, x2=18.33, 误差是:0.88
迭代次数是:4, x1=21.02, x2=18.32, 误差是:0.03
迭代次数是:5, x1=21.02, x2=18.32, 误差是:0.00
目标函数的值是:2021.17
"""4.总结
内点法和单纯形法的结果(上一篇博客中最终的结果为5700,而内点法只有2021.27)相差较大,这是因为内点法的搜索路径在可行域的内部,而不可能在可行域的边上,这也是内点法的局限性。