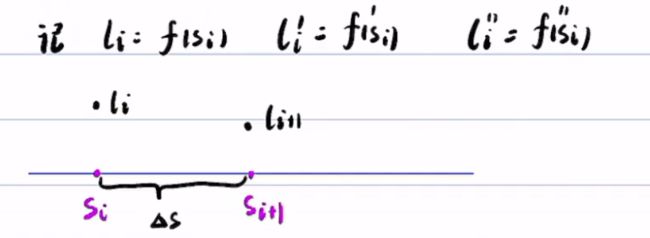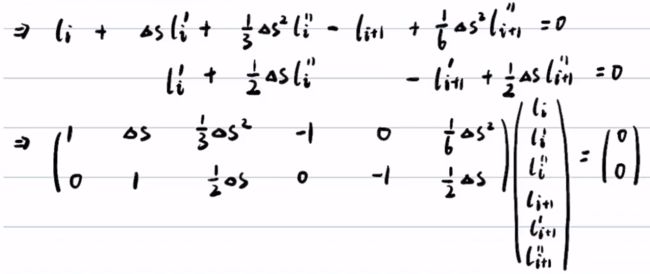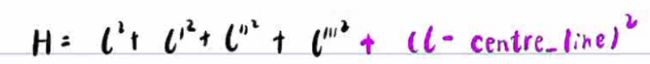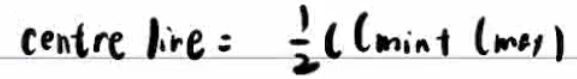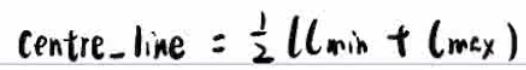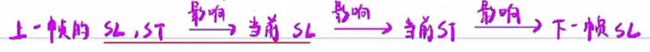自动驾驶决策规划算法第二章——Apollo EM Planner实践篇
前置学习内容:自动驾驶控制算法
【自动驾驶】【零基础】基础自动驾驶控制算法笔记_免费教学录影带的博客-CSDN博客
自动驾驶决策规划第一章
自动驾驶决策规划算法第一章_免费教学录影带的博客-CSDN博客_自动驾驶五次多项式
自动驾驶决策规划第二章——理论篇
自动驾驶决策规划算法第二章——Apollo EM Planner理论篇_免费教学录影带的博客-CSDN博客
4、代码实践部分
(1)感知模块搭建
首先是感知模块的搭建。由于要避障,所以需要感知,需要看到障碍物
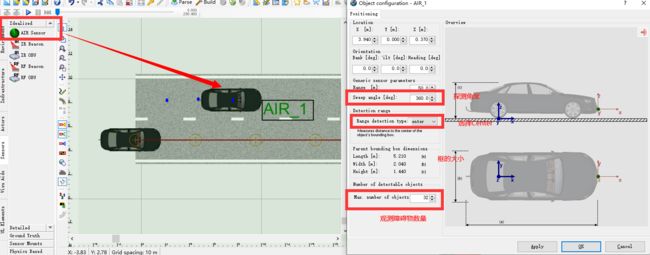
首先来到prescan加传感器,这里选择AIR理想传感器,注意这里还要把范围改成60m
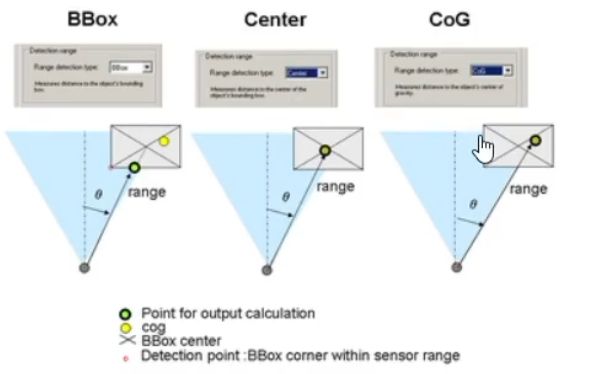
Prescan探测到障碍物会将其用矩形框框出来,没办法给出障碍物准确位置,是一种简化计算。矩形框中心和障碍物中心不一定一致,BBox输出框的外围信息,Center输出框中心,CoG输出重心,这里选择Center。
Prescan处理动态障碍物的坐标系与我们的不一样,它以北为正坐标轴,以北为0°,而世界坐标系是以东为0°,下面代码要进行转换
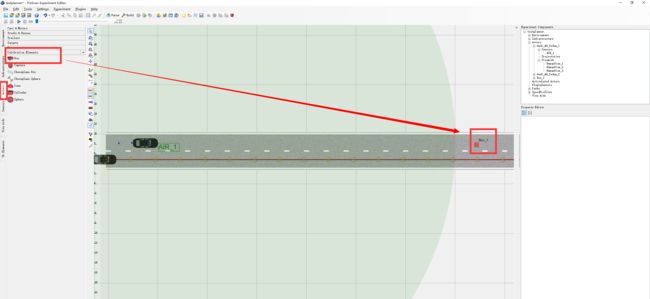
接下来放置障碍物,在探测范围外面
确定传感器与车的相对位置 ,拖放一个box在车上
其x为11.6,车的坐标为9.48。
车的位置和传感器相对位置大概是2.16,因此需要在判断障碍物的坐标时要加上2.16。(个人理解,这里把车原点绕着2.16半径的圆,保证圆内无障碍物)
接下来build然后regenerate回到matlab
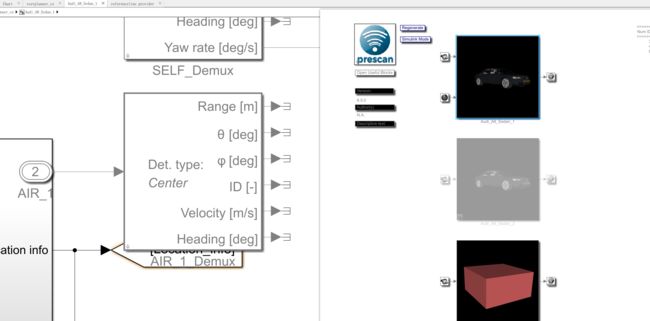
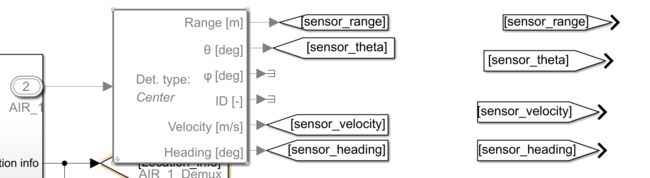
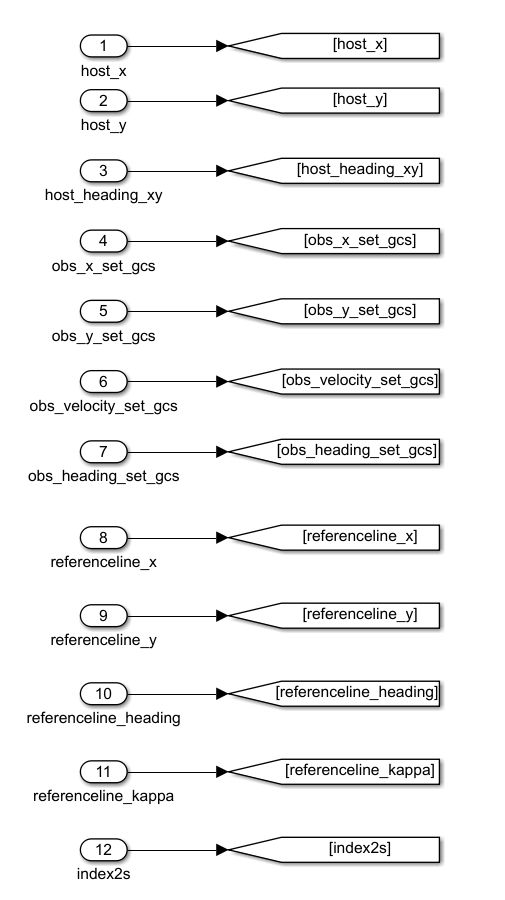
首先可以看到上面设置的AIR传感器的输出,先处理输出数据(障碍物在传感器坐标系下的极坐标range,theta,障碍物的速度大小velocity,障碍物的速度方向与x轴的夹角heading)
先把输出的数据拉出来,准备进行坐标转换
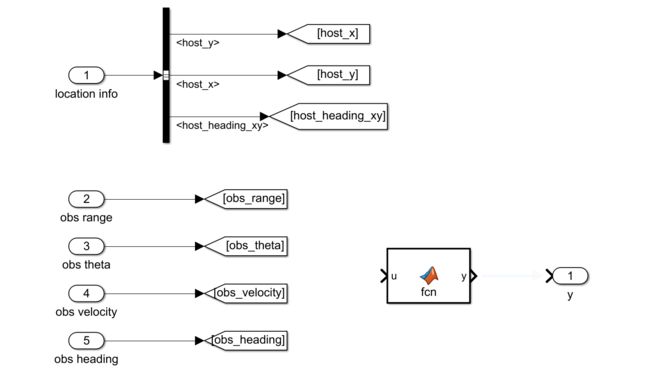
新建一个子模块来处理,输入定位信息,当前车的位置xy以及方向heading
去外面把线都连进来,输入为location info和传感器信息
接下来写一个函数来处理传感器信息,输出障碍物的位置速度以及方向
function [obs_x_set_gcs,obs_y_set_gcs,obs_velocity_set_gcs,obs_heading_set_gcs] = ...
fcn(host_x,host_y,host_heading_xy,obs_range,obs_theta,obs_velocity,obs_velocity_heading)
%gcs 全局坐标系global coordinate system
%该函数是感知模块,输出障碍物的位置,速度大小,速度方向与世界坐标系x轴的夹角
% 输入:定位信息host_x, host_y, host_heading_xy 世界坐标系
% 障碍物在传感器坐标系下的极坐标range,theta
% 障碍物的速度大小velocity
% 障碍物的速度方向与x轴的夹角heading
% 输出:障碍物在世界坐标系下的坐标x y v v与x轴的夹角heading
% 注意输出的heading是障碍物的速度heading,不是障碍物的几何heading。是障碍物速度方向不是障碍物几何方向
% 几何heading并不重要,因为prescan会用一个框表示
%传感器最多输出32个障碍物信息,但是事先不知道有多少个障碍物,所以要做个缓冲
% %输出初始化
obs_x_set_gcs = ones(32,1) * nan;
obs_y_set_gcs = ones(32,1) * nan;
obs_velocity_set_gcs = ones(32,1) * nan;
obs_heading_set_gcs = ones(32,1) * nan;
% %传感器极坐标的角度顺时针为正,世界坐标是逆时针为正
theta_transfer = -obs_theta * pi/180; %再加上角度转弧度
% %速度的方向以北为0°,世界坐标系是以东为0°
heading_transfer = (-obs_velocity_heading + 90 * ones(32,1)) * pi/180;
% % 世界坐标系下障碍物距离车的x和y距离
x_transfer = obs_range .* cos(theta_transfer + host_heading_xy);
y_transfer = obs_range .* sin(theta_transfer + host_heading_xy);
%计算障碍物的世界坐标
for i = 1:32
if obs_range(i) ~= 0
obs_x_set_gcs(i) = x_transfer(i) + host_x + 2.16*cos(host_heading_xy);
obs_y_set_gcs(i) = y_transfer(i) + host_y + 2.16*sin(host_heading_xy);
obs_heading_set_gcs(i) = heading_transfer(i);
obs_velocity_set_gcs(i) = obs_velocity(i);
end
end
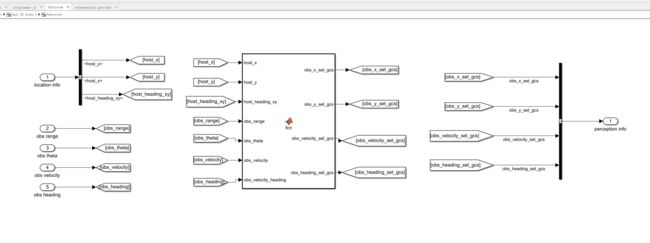
这样感知模块就写完了,我们现在获得了障碍物在全局坐标系下的位置,速度以及方向,将他们打包输出出去,作为perception info
(2)规划信号前处理
接下来进行规划模块预处理
定位模块加入加速度
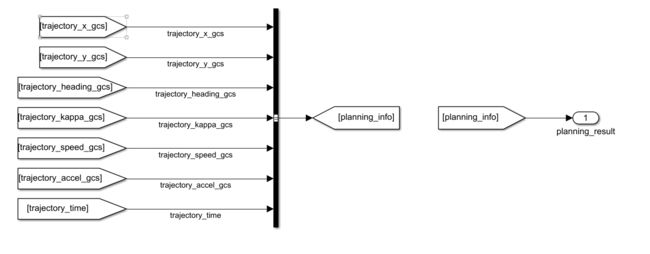
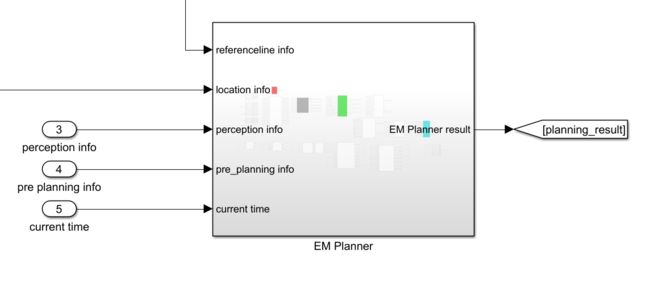
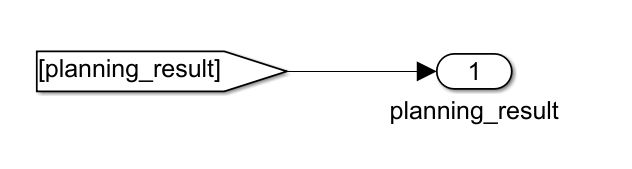
进入planning模块,增加planning_result输出
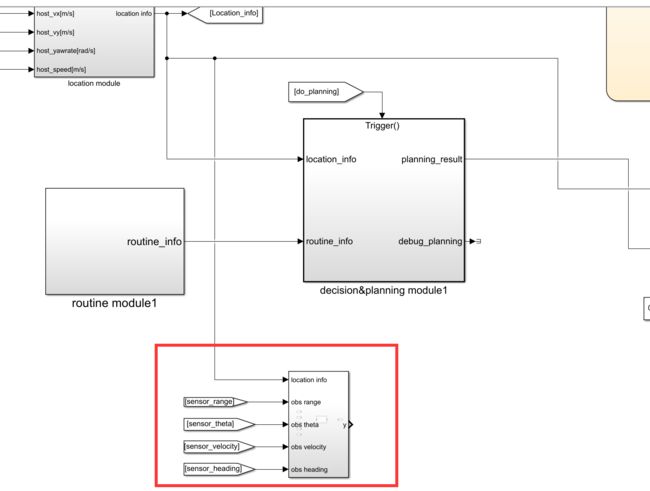
决策规划模块增加三个输入,感知信息,上次规划信息以及当前时间,
当前时间使用time模块
![]()
将输出的result加延迟1s作为上个处理结果输入给决策规划模块
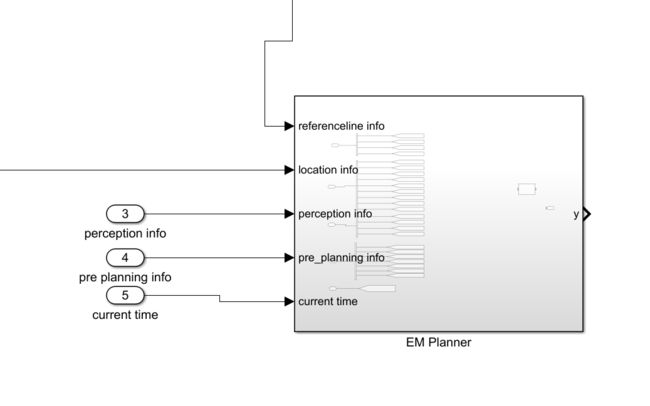
然后新建EM Planner模块,把输入信息加进去
将该有的输入输入进去整理好
至此,规划信号前处理完毕
(3)规划起点算法
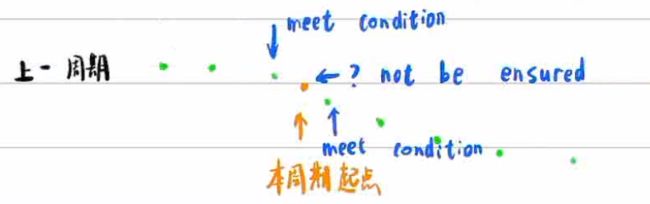
决策规划的第一步是确立规划起点,根据上一节的结论,分为第一次运行和不是第一次运行,第一次运行的时候以当前车位置为起点,后面再运行的时候以上次规划的结果,本周期的规划起点为
新建一个函数确定起点并拼接上一段规划的轨迹
接下来写一下函数,算法运行流程如下:如果是第一次运行,获取当前车辆的信息作为规划起点,然后设置规划时间为0+100ms;如果不是第一次运行,说明我们已经有上个周期的轨迹了,这个轨迹是带有时间戳信息的,根据当前时间可以查到车辆根据上个轨迹应该所处的位置(pre_x_desire,pre_y_desire),然后计算当前位置和上个周期该时间对应位置之间的横纵向误差lon_err和lat_err,如果纵向误差大于2.5,横向误差大于0.5,则认为控制没跟上,这种情况我们使用车辆动力学模型推出规划起点(这里使用质点模型外推)(注意:这里推出来的是当前时间往后100ms的位置作为规划起点)。如果误差合理,我们认为上个周期该时间对应位置作为规划起点,接下来计算拼接轨迹,假设pre_trajectory_time的第j个等于当前周期后100ms,如果j大于20,就把j-19到j这20个轨迹点提取出来作为拼接轨迹,如果j小于20,就从起点开始能拼多少就多少个。
最终可以得到规划起点以及拼接轨迹。
function [plan_start_x,plan_start_y,plan_start_heading,plan_start_kappa,plan_start_vx,plan_start_vy,plan_start_ax,plan_start_ay,...
plan_start_time,stitch_x,stitch_y,stitch_heading,stitch_kappa,stitch_speed,stitch_accel,stitch_time] = ...
fcn(pre_trajectory_x,pre_trajectory_y,pre_trajectory_heading,pre_trajectory_kappa,pre_trajectory_velocity,...
pre_trajectory_accel,pre_trajectory_time,current_time,host_x,host_y,host_heading_xy,host_vx,host_vy,host_ax,host_ay)
% 该函数将计算规划的起点以及拼接轨迹的信息
% 输入 上一周期的规划结果信息pre_trajectory x , y, heading, kappa,velocity, accel,time
% 本周期的绝对时间current_time
% 定位信息host x, y, heading, kappa,vx,vy, ax, ay
% 输出 规划起点信息plan_start x, y, heading, kappa, vx,vy, ax, ay(vx, vy, ax, ay)是世界坐标系的
% 待拼接的轨迹信息,一般在上一周期的轨迹中的current_time+100ms,往前取20个点。
% 当规划完成后,本周期的规划结果和stitch_trajectory一起拼好发给控制
%输出初始化
stitch_x = zeros(20,1);
stitch_y = zeros(20,1);
stitch_heading = zeros(20,1);
stitch_kappa = zeros(20,1);
stitch_speed = zeros(20,1);
stitch_accel = zeros(20,1);
% 时间为负代表没有对应的拼接轨迹
stitch_time = zeros(20,1)*-1;
%声明全局变量
persistent is_first_run;
if isempty(is_first_run)
%代表代码首次运行
is_first_run = 0;
% 按照轨迹拼接算法,应该用车辆动力学递推,但是首次运行车辆的速度都是0,所以没必要递推了
plan_start_x = host_x;
plan_start_y = host_y;
plan_start_heading = host_heading_xy;
plan_start_kappa = 0;
plan_start_vx = 0;
plan_start_vy = 0;
plan_start_ax = 0;
plan_start_ay = 0;
%规划的起点的时间应该是当前的时间+100ms
plan_start_time = current_time + 0.1;
else
%该函数不是首次运行
x_cur = host_x;
y_cur = host_y;
heading_cur = host_heading_xy;
kappa_cur = 0;
%vx vy ax ay 要转换成世界坐标系
vx_cur = host_vx * cos(heading_cur) - host_vy * sin(heading_cur);
vy_cur = host_vx * sin(heading_cur) + host_vy * cos(heading_cur);
ax_cur = host_ax * cos(heading_cur) - host_ay * sin(heading_cur);
ay_cur = host_ax * sin(heading_cur) + host_ay * cos(heading_cur);
% 规划周期
dt = 0.1;
%由于不是首次运行,有上个时刻的轨迹了,找到上一周期轨迹规划的本周期车辆应该在的位置
for i = 1: length(pre_trajectory_time)
if(pre_trajectory_time(i) <= current_time && pre_trajectory_time(i+1)>current_time)
break;
end
end
%上一周期规划的本周期的车应该在的位置
pre_x_desire = pre_trajectory_x(i);
pre_y_desire = pre_trajectory_y(i);
pre_heading_desire = pre_trajectory_heading(i);
%计算横纵向误差
% 切向量
tor = [cos(pre_heading_desire);sin(pre_heading_desire)];
%法向量
nor = [-sin(pre_heading_desire);cos(pre_heading_desire)];
%误差向量
d_err = [host_x;host_y] - [pre_x_desire;pre_y_desire];
%纵向误差
lon_err = abs(d_err' * tor);
%横向误差
lat_err =abs(d_err' * nor);
%纵向误差大于2.5,横向误差大于0.5,认为控制没跟上
if(lon_err>2.5 || lat_err > 2.5)
%此分支处理控制未跟上的情况:规划起点使用运动学(质点模型)外推
plan_start_x = x_cur + vx_cur * dt + 0.5 * ax_cur * dt *dt;
plan_start_y = y_cur + vy_cur * dt + 0.5 * ay_cur * dt *dt;
plan_start_vx = vx_cur + ax_cur*dt;
plan_start_vy = vy_cur + ay_cur*dt;
plan_start_ax = ax_cur;
plan_start_ay = ay_cur;
plan_start_kappa = kappa_cur;
plan_start_time = current_time + 0.1;
else
% 此分支表示控制能跟的上的规划,开始拼接
for j = 1:length(pre_trajectory_time)
if(pre_trajectory_time(j) <= current_time +0.1 && pre_trajectory_time(j+1)>current_time +0.1)
break;
end
end
%注:此算法要能运行需要trajectory的点有很高的密度
plan_start_x = pre_trajectory_x(j);
plan_start_y = pre_trajectory_y(j);
plan_start_heading = pre_trajectory_heading(j);
plan_start_kappa = pre_trajectory_kappa(j);
% 这里的pre_trajectory的速度和加速度是指轨迹的切向速度,切向加速度
plan_start_vx = pre_trajectory_velocity(j) * cos(plan_start_heading);
plan_start_vy = pre_trajectory_velocity(j) * sin(plan_start_heading);
%pre_trajectory的加速度是切向加速度,要想计算ax,ay还要计算法向加速度
%计算轨迹在current_time+100ms这个点的切向量法向量
tor = [cos(plan_start_heading);sin(plan_start_heading)];
nor = [-sin(plan_start_heading);cos(plan_start_heading)];
a_tor = pre_trajectory_accel(j) * tor;
a_nor = pre_trajectory_velocity(j)^2 * plan_start_kappa * nor;
plan_start_ax = a_tor(1) + a_nor(1);
plan_start_ay = a_tor(2) + a_nor(2);
plan_start_time = pre_trajectory_time(j);
% 计算拼接轨迹
%j 表示 current_time + 0.1的时间点在 pre_trajectory_time的编号
%拼接是往从j开始,往前拼接20个,也就是pre_trajectory(j-1),j-2,j-3,... .j-19
%分两种情况,如果j小于20,意味着前面的轨迹点不够20个
%如果j >= 20,意味着前面的点多于20个
%还有一个细节需要考虑,pre_trajectory x(j) y(j) ....是规划的起点,那么在轨迹拼接时
%需不需要在stitch_trajectory中把pre_trajectory x(j) y(j) ....包含进去
%答案是否定的,不应该包进去,因为规划的起点会在规划模块计算完成后的结果中包含,如果在拼接的时候
%还要包含,那就等于规划起点包含了两次
%除非本周期计算的轨迹不包含规划起点,那么stitch_trajectory可以包含规划起点。
%如果本周期计算的轨迹包含规划起点,那么stitch_trajectory就不可以包含规划起点。
%我们选择规划包含起点,拼接不包含起点的做法
%把起点去掉
j = j - 1;
if j >= 20
stitch_x = pre_trajectory_x(j-19:j);
stitch_y = pre_trajectory_y(j-19:j);
stitch_heading = pre_trajectory_heading(j-19:j);
stitch_kappa = pre_trajectory_kappa(j-19:j);
stitch_speed = pre_trajectory_velocity(j-19:j);
stitch_accel = pre_trajectory_accel(j-19:j);
stitch_time = pre_trajectory_time(j-19:j);
else %能拼多少就拼多少个
stitch_x(20-j+1:20) = pre_trajectory_x(1:j);
stitch_y(20-j+1:20) = pre_trajectory_y(1:j);
stitch_heading(20-j+1:20) = pre_trajectory_heading(1:j);
stitch_kappa(20-j+1:20) = pre_trajectory_kappa(1:j);
stitch_speed(20-j+1:20) = pre_trajectory_velocity(1:j);
stitch_accel(20-j+1:20) = pre_trajectory_accel(1:j);
stitch_time(20-j+1:20) = pre_trajectory_time(1:j);
end
end
end
接下来连接输入输出
(4)index2s算法
接下来做的是把直角坐标转化为自然坐标,规划起点和障碍物都是以世界坐标给定的,都需要投影到参考线上(自然坐标),坐标转换之前已经讲过了,直接套公式即可,比较麻烦的是求s,因为需要不停叠加,如果有10个障碍物,每个障碍物的s都需要叠加,希望找到一种快速计算s的方法。因为参考线referenceline是一堆离散点,所以可以实现找到离散点编号对应的s,比如1号点对应s=0,2号点s对应0.1之类的,三号点s对应0.3。有了这个对应关系,算s就比较简单了,因为障碍物要计算匹配点,前面已经求过了匹配点的编号,所以一旦有了匹配点的编号可以立刻得到s是什么,有了匹配点的s再计算投影点的s就比较简单了,对于障碍物越多的情况越显著。
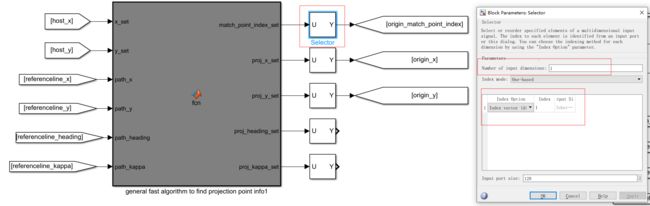
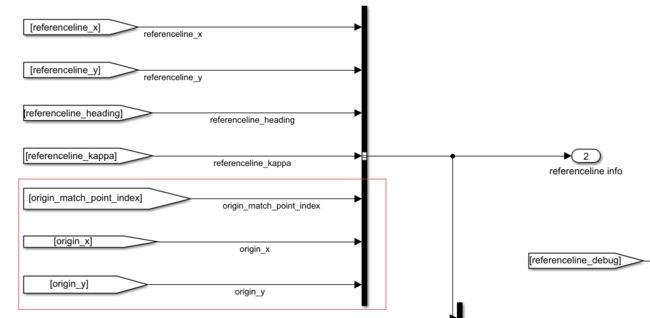
所以我们要做这个表,命名为:index2s表。在制作之前,首先要确定自然坐标系的坐标原点的x,y。因为一般来说自然坐标系的原点不是以referenceline的第一个点为坐标原点,一般是以车辆定位投影到referenceline上的投影点作为坐标原点,这样的话index是负数,我们要先计算坐标原点的x和y,然后再去计算index和s的对应表。
打开referenceline provider模块,把批量处理投影点模块复制一份,然后把车辆当前位置以及参考线信息输入进去,输出接上一个选择第一个index的selector,获取第一个元素。
然后使用bus输出出去
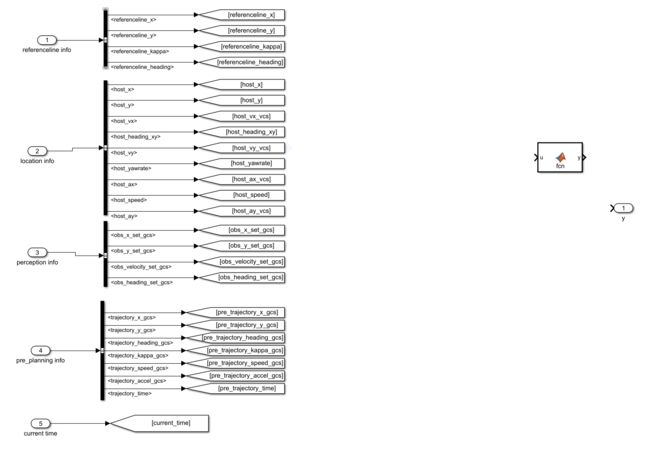
回到EM Planner模块,处理一下info
接下来新建一个function来写index2s函数
function index2s = fcn(path_x, path_y, origin_x, origin_y, origin_match_point_index)
%该算法将计算出index与s的转换关系,index2s(i)表示当编号为i时,对应的弧长s
n = 181; %参考线有180个点,所以index2s也是180
index2s = zeros(n,1);
%这个循环计算的是以轨迹起点为坐标原点的index2s的转换关系
for i = 2:181
index2s(i) = sqrt((path_x(i) - path_x(i-1))^2 + (path_y(i) - path_y(i-1))^2) + index2s(i-1);
end
% 在计算起点到坐标原点的弧长s0,减去s0,就得到了以给定坐标原点为起点的index2s的关系
s0 = CalcSFromIndex2S(index2s,path_x, path_y,origin_x, origin_y, origin_match_point_index);
%计算完s0再用原index2s减去s0
index2s = index2s - ones(n,1) * s0;
end
function s = CalcSFromIndex2S(index2s,path_x, path_y,proj_x, proj_y, proj_match_point_index)
%该函数将计算给定index2s的映射关系后,计算点(proj_x, proj_y)所对应的弧长
%判断投影点在匹配点的前面还是后面,向量的内积可以判断前后
vector_1 = [proj_x; proj_y] - [path_x(proj_match_point_index);path_y(proj_match_point_index)];% 投影点和匹配点之间的误差的向量
% 匹配点的切线的方向向量vector_2,使用匹配点和匹配点前面的一个点之间的向量做近似
if proj_match_point_index < length(path_x) % 说明不是最后一个点
vector_2 = [path_x(proj_match_point_index+1);path_y(proj_match_point_index+1)] - ...
[path_x(proj_match_point_index);path_y(proj_match_point_index)];
else % 如果是最后一个点,就拿这个点减去前面那个点
vector_2 = [path_x(proj_match_point_index);path_y(proj_match_point_index)] - ...
[path_x(proj_match_point_index-1);path_y(proj_match_point_index-1)];
end
%使用向量内积判断投影点在匹配点的前面还是后面
if vector_1' * vector_2 > 0
% 投影点在匹配点的前面
s = index2s(proj_match_point_index) + sqrt(vector_1' * vector_1);
else
% 投影点在匹配点的后面
s = index2s(proj_match_point_index) - sqrt(vector_1' * vector_1);
end
end有了这个模块,就不需要每次去加载,只需要查表就可以获取s
![]()
(5)规划起点的坐标转换
接下来要把规划起点转换到SL坐标系
首先求投影点,之前写过了,直接复制过来用
![]()
接下来进行坐标转换
新建一个函数,创建子系统
对于静态障碍物,只需要s和l即可,对于\dot{s},\dot{l}这些不关心。如果对于动态障碍物来说,需要输出\dot{s},\dot{l}这些,而对于规划起点,还需要加速度信息,不仅要\dot{s},\dot{l},还需要\ddot{s},\ddot{l},不同的变量对于坐标转换的要求不同,我们写一个通用的算法
首先设置输入
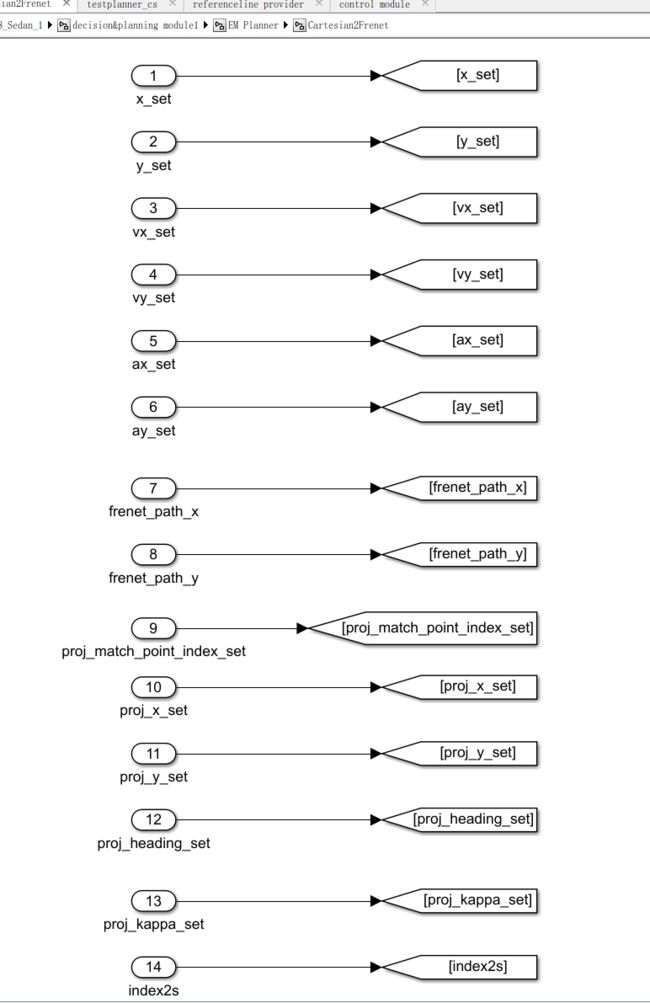
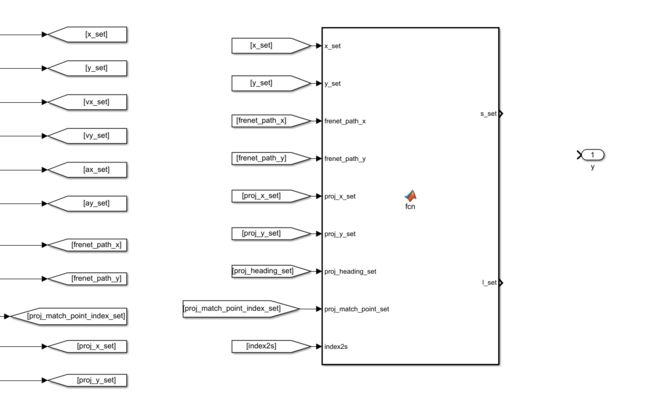
然后先写转s和l的算法
function [s_set,l_set] = fcn(x_set,y_set,frenet_path_x,frenet_path_y,...
proj_x_set, proj_y_set, proj_heading_set, proj_match_point_set,index2s)
% 该函数将计算世界坐标系下的x_set,y_set上的点在frenet_path下的坐标s 1
% 输入x_set, y_set待坐标转换的点
% frenet_path_x,frenet_path_y frenet坐标轴
% proj_x, y, heading, kappa,proj_match_point_index待坐标转换的点的投影点的信息
% index2s frenet_path的index与s的转换表
%由于不知道有多少个点需要做坐标转换,所以需要做缓冲
n = 128;%最多处理128个点
%输出初始化
s_set = ones(n,1)*nan;
l_set = ones(n,1)*nan;
for i = 1:length(x_set)
if isnan(x_set(i))
break;
end
%计算s,写个子函数
s_set(i) = CalcSFromIndex2S(index2s,frenet_path_x,frenet_path_y,proj_x_set(i), proj_y_set(i),...
proj_match_point_set(i));
n_r = [-sin(proj_heading_set(i));cos(proj_heading_set(i))];
r_h = [x_set(i);y_set(i)];
r_r = [proj_x_set(i);proj_y_set(i)];
l_set(i) = (r_h - r_r)' * n_r;
end
function s = CalcSFromIndex2S(index2s,path_x, path_y,proj_x, proj_y, proj_match_point_index)
%该函数将计算给定index2s的映射关系后,计算点(proj_x, proj_y)所对应的弧长
%判断投影点在匹配点的前面还是后面,向量的内积可以判断前后
vector_1 = [proj_x; proj_y] - [path_x(proj_match_point_index);path_y(proj_match_point_index)];% 投影点和匹配点之间的误差的向量
% 匹配点的切线的方向向量vector_2,使用匹配点和匹配点前面的一个点之间的向量做近似
if proj_match_point_index < length(path_x) % 说明不是最后一个点
vector_2 = [path_x(proj_match_point_index+1);path_y(proj_match_point_index+1)] - ...
[path_x(proj_match_point_index);path_y(proj_match_point_index)];
else % 如果是最后一个点,就拿这个点减去前面那个点
vector_2 = [path_x(proj_match_point_index);path_y(proj_match_point_index)] - ...
[path_x(proj_match_point_index-1);path_y(proj_match_point_index-1)];
end
%使用向量内积判断投影点在匹配点的前面还是后面
if vector_1' * vector_2 > 0
% 投影点在匹配点的前面
s = index2s(proj_match_point_index) + sqrt(vector_1' * vector_1);
else
% 投影点在匹配点的后面
s = index2s(proj_match_point_index) - sqrt(vector_1' * vector_1);
end
end
接下来写第二个模块,计算![]()
function [s_dot_set,l_dot_set,dl_set] = fcn(l_set,vx_set,vy_set,proj_heading_set,proj_kappa_set)
%该函数将计算frenet坐标系下的s_dot,l_dot, dl/ ds
n = 128;
%输出初始化
s_dot_set = ones(n,1 )*nan ;
l_dot_set = ones(n,1) *nan;
dl_set = ones (n,1)*nan;
for i = 1: length(l_set)
if isnan(l_set(i))
break
end
v_h = [vx_set(i);vy_set(i)];
n_r = [-sin(proj_heading_set(i)) ;cos(proj_heading_set(i))];
t_r = [cos(proj_heading_set(i)) ;sin(proj_heading_set(i))];
l_dot_set(i) = v_h'*n_r;
s_dot_set(i) = v_h'*t_r/(1 - proj_kappa_set(i)*l_set(i)) ;
%%%向量法做cartesian与frenet的转换要更简单,但是也有缺点,向量法必须依赖速度加速度
%l’= l_dot/s_dot但是如果s_dot = 0此方法就失效了
if abs(s_dot_set(i))<1e-6
dl_set(i) = 0;
else
dl_set(i) = l_dot_set(i)/s_dot_set(i);
end
end再写最后一个模块,计算s两点,l两点
function [s_dot2_set,l_dot2_set,ddl_set] = fcn(ax_set,ay_set,proj_heading_set,proj_kappa_set,l_set,s_dot_set,dl_set)
%由于不知道有多少个点需要做坐标转换,设一个最大值做缓冲
n = 128;
%输出初始化
s_dot2_set = ones(n,1)*nan;
l_dot2_set = ones(n,1)*nan;
ddl_set = ones(n,1) *nan;
for i = 1 : length(l_set)
if isnan(l_set(i))
break;
end
a_h = [ax_set(i) ;ay_set(i)];
n_r = [-sin(proj_heading_set(i)) ; cos(proj_heading_set(i))];
t_r = [cos(proj_heading_set(i)) ;sin(proj_heading_set(i)l;
%近似认为dkr/ds 为0简化计算
l_dot2_set(i) = a_h'*n_r - proj_kappa_set(i) * (1 - proj_kappa_set(i) * l_set(i)) * s_dot_set(i)^2;
s_dot2_set(i) = (1/(l - proj_kappa_set(i) * l_set(i)))* (a_h' * t_r + 2 * proj_kappa_set(i) * dl_set(i) * s_dot_set(i)^2;
%要考虑加速度为0的情况
if abs(s_dot2_set(i)) < 1e-6
ddl_set(i) = 0;
else
ddl_set(i) = (l_dot2_set(i) - dl_set(i)*s_dot2_set(i))/(s_dot_set(i)^2);
end
end
然后把所有输出整合起来
得到模块,连接输入输出
至此,得到规划起点的SL,接下来处理障碍物
(6)障碍物处理与坐标转换
新建一个函数来写
function [obs_x_set_final, obs_y_set_final, obs_velocity_set_final, obs_heading_set_final] = ...
fcn(host_x,host_y,host_heading_xy,obs_x_set_gcs,obs_y_set_gcs,obs_velocity_set_gcs,obs_heading_set_gcs)
%该函数将筛选障碍物,纵向[-10,60]横向[-10,10]的障碍物才会被考虑
%该函数只是一种单车道的临时办法,考虑到多车道情况,即使障碍物距离较远也应该考虑
%EM P1anner完全体是多车道并行计算的,每个车道都生成参考线然后并行计算出多条轨迹,再选择最优的轨迹作为输出
%传感器最多可以识别32个障碍物
n = 32;
%输出初始化
obs_x_set_final = ones(n,1) *nan ;
obs_y_set_final = ones(n,1) *nan;
obs_velocity_set_final = ones(n,1)*nan;
obs_heading_set_final = ones(n,1)*nan;
for i = 1: length(obs_x_set_gcs)
if isnan(obs_x_set_gcs(i))
break;
end
%自车的heading的方向向量与法向量
tor = [cos(host_heading_xy);sin(host_heading_xy)];
nor = [-sin(host_heading_xy) ; cos(host_heading_xy)] ;
%障碍物与自车的距离向量
vector_obs = [obs_x_set_gcs(i) ;obs_y_set_gcs(i)] - [host_x; host_y] ;
%障碍物纵向距离
lon_distance = vector_obs'*tor;
lat_distance = vector_obs'*nor;
if (lon_distance < 60) && (lon_distance > -10)&& (lat_distance > -10) && (lat_distance < 10)
obs_x_set_final(count) = obs_x_set_gcs (i);
obs_y_set_final(count) = obs_y_set_gcs(i);
obs_heading_set_final(count) = obs_heading_set_gcs(i);
obs_velocity_set_final (count) = obs_velocity_set_gcs(i);
count = count + 1;
end
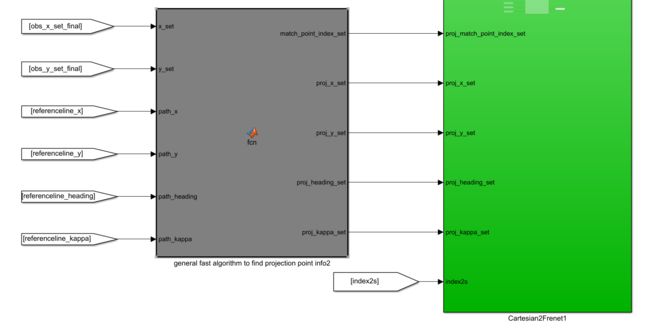
end接下来计算障碍物投影点
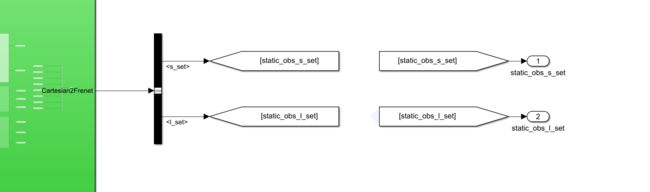
复制通用转换模块,然后把障碍物的信息作为xy输入进去,在输入给Cartesian2Frenet模块
注意,Cartesian2Frenet复制过来注释掉下面,我们只需要静态障碍物的s和l即可
最后把s和l使用bus输出出来,vx,vy,ax,ay都接地
此外还需要筛选一下静态障碍物和动态障碍物
新建一个函数
function [static_obs_x_set,static_obs_y_set,dynamic_obs_x_set, dynamic_obs_y_set,dynamic_obs_vx_set,dynamic_obs_vy_set] = ...
fcn(obs_x_set_gcs,obs_y_set_gcs,obs_heading_set_gcs,obs_velocity_set_gcs)
%该函数将分类静态障碍物和动态障碍物
%输出初始化
n = 32;
static_obs_x_set = ones(n,1)*nan;
static_obs_y_set = ones(n,1)*nan;
dynamic_obs_x_set = ones(n,1) *nan;
dynamic_obs_y_set = ones(n,1) *nan;
dynamic_obs_vx_set = ones (n,1)*nan;
dynamic_obs_vy_set = ones(n,1) *nan;
count_static = 1;
count_dynamic = 1;
for i = 1:length(obs_x_set_gcs)
if abs(obs_velocity_set_gcs(i))< 0.1
static_obs_x_set(count_static) = obs_x_set_gcs(i);
static_obs_y_set (count_static) = obs_y_set_gcs(i);
count_static = count_static + 1;
else
dynamic_obs_x_set (count_dynamic) = obs_x_set_gcs(i) ;
dynamic_obs_y_set(count_dynamic) = obs_y_set_gcs(i);
count_dynamic = count_dynamic + 1;
end
end
然后吧这些全部打包成一个子系统
设置输入和输出
到目前,动态规划之前的准备工作已经做完了,下面说正式的动态规划算法
(7)动态规划主算法
新建一个函数来写动态规划的代码
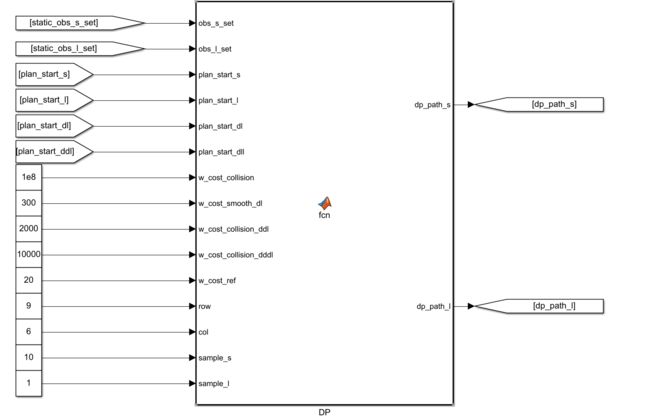
函数输入为规划起点信息,静态障碍物信息,以及动态规划系数
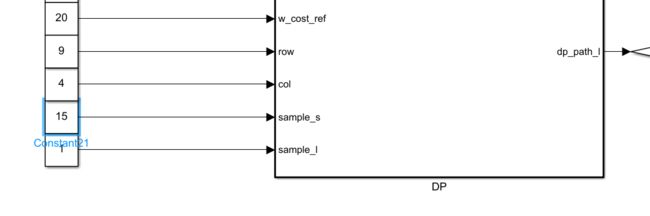
function [dp_path_s,dp_path_l] = fcn(obs_s_set,obs_l_set,plan_start_s,plan_start_l,...
plan_start_dl,plan_start_dll,w_cost_collision,w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref, row,col,sample_s,sample_l)
%该函数为路径决策算法动态规划的主函数
% 输入: obs s 1 set筛选后的障碍物s1信息
% plan_start s 1 d1 ddl规划起点信息
% w_cost_obs,w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref动态规划代价权重
% row col 动态规划采样点的行数和列数
% sample_s, sample_l 采样的s 1 长度
% 输出: dp_path_l, dp_path_dl, dp_path_s动态规划的路径s1
%动态规划最优的数据结构是结构体矩阵,但是simulink不支持结构体矩阵,所以动态规划算法写的相对难以理解
%声明二维矩阵变量node_cost,node_cost(i,j)表示从起点出发,到行i列j节点的最小代价为node_cost(i, j)
node_cost = ones(row, col)*inf ;
%初始化为无穷大
%声明二维矩阵变量pre_node_index pre_node_index(i,j)表示从起点到行i列j的节点的最优路径中前一个节点的行号为
%pre_node_index(i, j)
%例: 比如一条最优路径为起点 -> node(1,1) -> node(2,2) -> node(3,3)
%则 pre_node_index(3,3) = 2 (最优路径的前一个节点是node(2,2)取它的行号)
% pre_node_index(2,2)=1 (最优路径的前一个节点是node(1,1)取它的行号)
% pre_node_index(1,1) =0 (起点的行号默认是0)
% 其实pre_node_index就是当找到最小代价的路径后从终点到起点反向选择出最优路径的
%如果用结构体矩阵完全没有必要弄得这么麻烦,但是simulink不支持
pre_node_index = zeros(row,col);
%初始化,所有节点的上个最优节点的行号都是0,也就是起点
%先计算从起点到第一列的cost
for i = 1:row
% 使用一个子函数计算第一层的Cost
node_cost(i,1) = CalcStartCost(plan_start_s,plan_start_l,...
plan_start_dl,plan_start_dll,i,sample_s,sample_l,w_cost_collision,...
w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,...
obs_s_set,obs_l_set,row);
end
% 动态规划主代码
for j = 2:col
for i = 1 : row
%计算当前node(i,j)的s l
cur_node_s = plan_start_s + j *sample_s;
cur_node_l = ((row + 1)/2 - i) *sample_l;
%遍历前一列的节点
for k = 1 :row
%计算前一列节点的s l
pre_node_s = plan_start_s + (j - 1) * sample_s;
pre_node_l = ((row + 1)/2 - k) * sample_l;
cost_neighbour = CalcNeighbourCost(pre_node_s,pre_node_l,cur_node_s,cur_node_l,w_cost_collision,...
w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,obs_s_set,obs_l_set);
% 起点到上一个节点的最小代价为node_cost(k,j-1)
%再加上node(k,j-1)到node(i,j)的代价 (k = 1,2,3,4.. .row)中最小的
cost_temp = pre_min_cost + cost_neighbour ;
if cost_temp < node_cost(i,j)
node_cost(i,j) = cost_temp;
%把最优路径上一列节点的行号记录下来
pre_node_index(i,j)= k;
end
end
end
end
%找到node_cost最后一列中,cost最小的,记代价最小的行号为index
index = 0;
min_cost = inf;
for i = 1:row
if node_cost(i, end)< min_cost
min_cost = node_cost(i, end);
index = i ;
end
end
%动态规划最优路径初始化
dp_node_list_row = zeros(col, 1) ;
%从后往前逆推
cur_index = index ;
for i = 1:col
%记录cur_index前面节点的行号
pre_index = pre_node_index(cur_index, end - i + 1) ;
%把cur_index放到dp_node_list_row对应的位置
dp_node_list_row(col - i + 1) = cur_index;
%再把pre_index赋给cur_index进行下一步递推
cur_index = pre_index ;
end
%输出初始化,由于事先不知道横纵向的采样列数,因此需要做缓冲
dp_path_s = ones(15,1)*-1;
dp_path_l = ones(15,1)*-1;
for i = 1:col
dp_path_s(i) = plan_start_s + i *sample_s;
dp_path_l(i) = ((row + 1)/ 2 - dp_node_list_row(i)) * sample_l;
end
end
function cost = CalcNeighbourCost(pre_node_s,pre_node_l,cur_node_s,cur_node_l,w_cost_collision,...
w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,obs_s_set,obs_l_set)
% 该函数将计算相邻两个节点之间的cost
start_l = pre_node_l;
start_dl = 0;
start_ddl = 0;
% ...
% ...row = 3 中间的行号= (row + 1)/2 = 2
% ...
end_l = cur_node_l;
end_dl = 0;
end_ddl = 0;
start_s = pre_node_s;
end_s = cur_node_s;
coeff = CalcQuinticCoeffient(start_l, start_dl, start_ddl, end_l, end_dl, end_ddl, start_s, end_s);
a0 = coeff(1);
a1 = coeff(2);
a2= coeff(3);
a3 = coeff(4);
a4 = coeff(5);
a5 = coeff(6);
%取10个点计算cost
ds = zeros(10,1);
l = zeros(10,1);
dl = zeros(10,1);
ddl = zeros(10,1);
dddl = zeros (10,1);
for i = 1:10
ds(i) = start_s + (i-1)*sample_s/10;
end
l = a0 * ones (10,1) + a1* ds + a2 * ds.^2+ a3 * ds.^3 + a4 * ds.^4 + a5 * ds. 5;
dl = al * ones(10,1)+ 2* a2 * ds + 3 * a3 * ds.^2+ 4* a4 * ds.^3 +5 * a5 * ds.^4;
ddl = 2 * a2* ones(10,1)+6 * a3 * ds + 12 * a4 * ds.^2+ 20 * a5 * ds.^3;
dddl = 6 * ones(10,1) * a3 + 24 * a4 * ds + 60 * a5 * ds.^2;
cost_smooth = w_cost_smooth_dl * (dl'* dl) + w_cost_smooth_ddl * (ddl' * ddl) + w_cost_smooth_dddl * (dddl' * dddl);
cost_ref = w_cost_ref * (l' *l);
cost_collision = 0;
for i = 1:length(obs_s_set)
if isnan(obs_s_set(i))
break;
end
dlon = ones (10,1)* obs_s_set(i) - ds ;
dlat = ones(10,1)* obs_l_set(i) - l;
%这里做了非常简化的质点模型,认为障碍物就是一个点。(可以这么做的原因:动态规划不需要特别复杂,只需要开辟凸空间,具体避障要在二次规划中做)
square_d = dlon.^2 + dlat.^2; % 近似算法,并不是真正的距离,因为dx^2+dy^2不是距离
cost_collision_once = CalcObsCost(w_cost_collision,square_d) ;
cost_collision = cost_collision + cost_collision_once;
end
cost = cost_collision + cost_smooth + cost_ref;
end
function obs_cost = CalcObsCost(w_cost_collision,square_d)
%该函数将计算障碍物的距离代价
%暂定超过4米的cost为0在4到3米的cost为1000/squard_d,在小于3米的cost为w_cost_collisioncost = 0;
for i = 1 : length(square_d)
if (square_d(i)< 16 && square_d(i) > 9)
cost = cost + 1000/ square_d(i);
elseif (square_d(i)<9)
cost = cost + w_cost_collision;
end
end
obs_cost = cost;
end
function cost = CalcStartCost(begin_s,begin_l,begin_dl,begin_ddl,cur_node_row,sample_s,sample_l,...
w_cost_collision,w_cost_smooth_dl,w_cost_smooth_ddl,w_cost_smooth_dddl,w_cost_ref,...
obs_s_set,obs_l_set,row)
%该函数将计算起点到第一层的cost
start_l = begin_l;
start_dl = begin_dl;
start_ddl = begin_ddl;
% ...
% ...row = 3 中间的行号= (row + 1)/2 = 2
% ...
end_l = ((row + 1)/2 - cur_node_row)*sample_l;
end_dl = 0;
end_ddl = 0;
start_s = begin_s;
end_s = begin_s + sample_s;
coeff = CalcQuinticCoeffient(start_l, start_dl, start_ddl, end_l, end_dl, end_ddl, start_s, end_s);
a0 = coeff(1);
a1 = coeff(2);
a2= coeff(3);
a3 = coeff(4);
a4 = coeff(5);
a5 = coeff(6);
%取10个点计算cost
ds = zeros(10,1);
l = zeros(10,1);
dl = zeros(10,1);
ddl = zeros(10,1);
dddl = zeros (10,1);
for i = 1:10
ds(i) = start_s + (i-1)*(end_s - start_s)/10;
end
l = a0 * ones (10,1) + a1* ds + a2 * ds.^2+ a3 * ds.^3 + a4 * ds.^4 + a5 * ds. 5;
dl = al * ones(10,1)+ 2* a2 * ds + 3 * a3 * ds.^2+ 4* a4 * ds.^3 +5 * a5 * ds.^4;
ddl = 2 * a2* ones(10,1)+6 * a3 * ds + 12 * a4 * ds.^2+ 20 * a5 * ds.^3;
dddl = 6 * ones(10,1) * a3 + 24 * a4 * ds + 60 * a5 * ds.^2;
cost_smooth = w_cost_smooth_dl * (dl'* dl) + w_cost_smooth_ddl * (ddl' * ddl) + w_cost_smooth_dddl * (dddl' * dddl);
cost_ref = w_cost_ref * (l' *l);
cost_collision = 0;
for i = 1:length(obs_s_set)
if isnan(obs_s_set(i))
break;
end
dlon = ones (10,1)* obs_s_set(i) - ds ;
dlat = ones(10,1)* obs_l_set(i) - l;
%这里做了非常简化的质点模型,认为障碍物就是一个点。(可以这么做的原因:动态规划不需要特别复杂,只需要开辟凸空间,具体避障要在二次规划中做)
square_d = dlon.^2 + dlat.^2; % 近似算法,并不是真正的距离,因为dx^2+dy^2不是距离
cost_collision_once = CalcObsCost(w_cost_collision,square_d) ;
cost_collision = cost_collision + cost_collision_once;
end
cost = cost_collision + cost_smooth + cost_ref;
end
function obs_cost = CalcObsCost(w_cost_collision,square_d)
%该函数将计算障碍物的距离代价
%暂定超过4米的cost为0在4到3米的cost为1000/squard_d,在小于3米的cost为w_cost_collisioncost = 0;
for i = 1 : length(square_d)
if (square_d(i)< 16 && square_d(i) > 9)
cost = cost + 1000/ square_d(i);
elseif (square_d(i)<9)
cost = cost + w_cost_collision;
end
end
obs_cost = cost;
end
function coeff = CalcQuinticCoeffient(start_l, start_dl, start_ddl, end_l, end_dl, end_ddl, start_s, end_s)
% l = a0 + a1*s + a2*s ^2 + a3*s ^3 + a4*s^4 + a5*s^5
% l’ = a1+ 2* a2* s + 3 * a3 * s ^2+ 4 * a4 * s^3 +5*a5 * s ^4
% l''= 2* a2+ 6 * a3 * s + 12 * a4 * s ^2+20 * a5 * s^3
start_s2 = start_s * start_s;
start_s3 = start_s2 * start_s;
start_s4 = start_s3 * start_s;
start_s5 = start_s4 * start_s;
end_s2 = end_s * end_s;
end_s3 = end_s2 * end_s;
end_s4 = end_s3 * end_s;
end_s5 = end_s4 * end_s;
A = [1, start_s, start_s2, start_s3, start_s4, start_s5;
0 1, 2*start_s, 3 * start_s2, 4 *start_s3, 5*start_s4;
0 0, 2, 6 * start_s, 12 *start_s2, 20*start_s3;
1, end_s, end_s2, end_s3, end_s4, end_s5;
0 1, 2*end_s, 3 * end_s2, 4 *end_s3, 5*end_s4;
0 0, 2, 6 * end_s, 12 *end_s2, 20*end_s3;];
B = [start_l;
start_dl;
start_ddl;
end_l;
end_dl;
end_ddl;
];
coeff = A/B;
end
连接好输入输出
注意这里设置9行6列,行数必须为奇数。纵向采样长度sample_s=10代表每10m采样1列,6列正好是60m,传感器探测范围也就是60m。横向采样长度sample_l为1m。行与行之间间距10m,列与列之间间距1m。
(8)后处理
动态规划完毕后,需要后处理
这里的dp_path_s和dp_path_l太少了,只反映了五次多项式的起点和终点,还不能称之为合格的轨迹,所以需要多采样几个点,增密变成合格的轨迹。
function [dp_path_s_final,dp_path_l_final,dp_path_dl_final,dp_path_ddl_final] = fcn(...
dp_path_s_init,dp_path_l_init,plan_start_s,plan_start_l,plan_start_dl,plan_start_ddl)
%该函数将增密dp_path_s, dp_path_l
%由于事先不知道动态规划采样的行和列,也就不知道动态规划计算的曲线有多长,因此需要做缓冲
%每1“米”采样一个点,一共采60个
ds = 1;
%输出初始化
dp_path_s_final = ones(60,1) * nan;
dp_path_l_final = ones(60,1) * nan;
dp_path_dl_final =ones(60,1) * nan;
dp_path_ddl_final =ones(60,1) * nan;
%设置五次多项式的起点
start_s = plan_start_s;
start_l = plan_start_l;
start_dl = plan_start_dl ;
start_ddl = plan_start_ddl ;
s_cur = [];
l_temp = [];
dl_temp =[];
ddl_temp = [];
% 每1m采样一次,直到多项式终点,退出循环
for i = 1 : length(dp_path_s_init)
if dp_path_s_init(i) ==-1
break;
end
for j = 1: 10000
%采样s
s_node = start_s + ds*(j - 1) ;
if s_node < dp_path_s_init(i)
s_cur = [s_cur,s_node];
else
break
end
end
end_s = dp_path_s_init(i) ;
end_l = dp_path_l_init(i) ;
end_dl = 0;
end_ddl = 0;
coeff = CalcQuinticCoeffient(start_l, start_dl, start_ddl, end_l, end_dl, end_ddl, start_s, end_s);
a0 = coeff(1);
a1 = coeff(2);
a2= coeff(3);
a3 = coeff(4);
a4 = coeff(5);
a5 = coeff(6);
l = a0 * ones(1, length(s_cur)) + a1 * s_cur + a2 * s_cur.^2 + a3 * s_cur.^3 +...
a4 * s_cur.^4 + a5 * s_cur.^5;
dl = a1 * ones(1,length(s_cur)) + 2 *a2 * s_cur + 3 * a3 * s_cur.^2 + ...
4 * a4 * s_cur.^3 +5 * a5* s_cur.^4;
ddl = 2 * a2 * ones(1,length(s_cur)) + 6 * a3 * s_cur + 12 * a4 * s_cur.^2 + ...
20 * a5 * s_cr.^3;
%把l dl ddl的结果保存
l_temp = [l_temp,1];
dl_temp = [dl_temp, dl];
ddl__temp = [ddl_temp, ddl];
% end的值赋值给start做下一步循环
start_s = end_s;
start_l = end_l;
start_dl = end_dl;
start_ddl = end_ddl;
s_cur = [];% 每次算完五次多项式后清空
end
for k = 1:length(l_temp)
if k == 61
break;
end
dp_path_s_final(k) = plan_start_s + ds * (k - 1) ;
dp_path_l_final(k)= l_temp(k);
dp_path_dl_final(k) = dl_temp(k) ;
dp_path_ddl_final(k) = ddl_temp(k);
end
end
function coeff = CalcQuinticCoeffient(start_l, start_dl, start_ddl, end_l, end_dl, end_ddl, start_s, end_s)
% l = a0 + a1*s + a2*s ^2 + a3*s ^3 + a4*s^4 + a5*s^5
% l’ = a1+ 2* a2* s + 3 * a3 * s ^2+ 4 * a4 * s^3 +5*a5 * s ^4
% l''= 2* a2+ 6 * a3 * s + 12 * a4 * s ^2+20 * a5 * s^3
start_s2 = start_s * start_s;
start_s3 = start_s2 * start_s;
start_s4 = start_s3 * start_s;
start_s5 = start_s4 * start_s;
end_s2 = end_s * end_s;
end_s3 = end_s2 * end_s;
end_s4 = end_s3 * end_s;
end_s5 = end_s4 * end_s;
A = [1, start_s, start_s2, start_s3, start_s4, start_s5;
0 1, 2*start_s, 3 * start_s2, 4 *start_s3, 5*start_s4;
0 0, 2, 6 * start_s, 12 *start_s2, 20*start_s3;
1, end_s, end_s2, end_s3, end_s4, end_s5;
0 1, 2*end_s, 3 * end_s2, 4 *end_s3, 5*end_s4;
0 0, 2, 6 * end_s, 12 *end_s2, 20*end_s3;];
B = [start_l;
start_dl;
start_ddl;
end_l;
end_dl;
end_ddl;
];
coeff = A/B;
end
算法写好后,连接输入输出
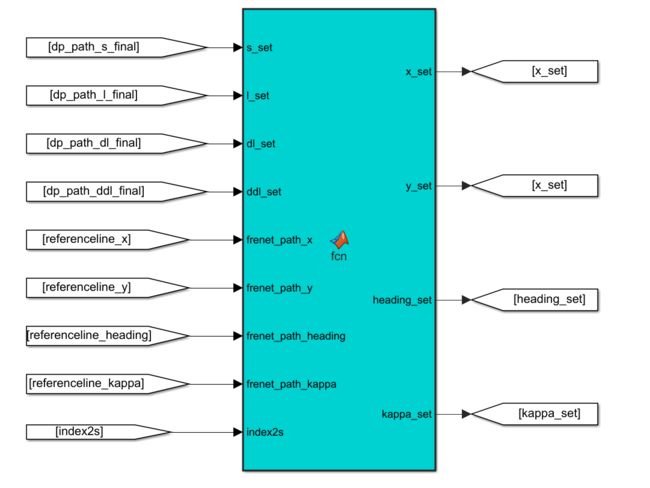
接下来要把path转回去,转到直角坐标系上去,发给控制去用
function [x_set,y_set,heading_set,kappa_set] = ...
fcn(s_set,l_set,dl_set,ddl_set,frenet_path_x,frenet_path_y,frenet_path_heading,frenet_path_kappa,index2s)
%通用算法frenet转frenet
%由于不知道有多少个(s,l)要转化成直角坐标,因此做缓冲
%输出初始化
x_set = ones (128,1) *nan;
y_set = ones (128,1) *nan;
heading_set = ones (128,1)*nan;
kappa_set = ones (128,1) *nan;
for i = 1 : length(s_set)
if isnan(s_set(i))
break;
end
%计算(s,l)在frenet坐标轴上的投影
[proj_x,proj_y,proj_heading, proj_kappa] = CalcProjPoint(s, frenet_path_x, frenet_path_y, frenet_path_heading,...
frenet_path_kappa,index2s);
nor = [-sin(proj_heading) ;cos(proj_heading)];
point = [proj_x ; proj_y] + l_set(i) *nor;
x_set(i) = point(1);
y_set(i) = point(2) ;
heading_set(i) = proj_heading + atan(dl_set(i)/(l - proj_kappa * l_set(i)));
% 近似认为kappa' == 0, frenet转cartesian见那个博客
kappa_set(i) = ((ddl_set(i) + proj_kappa * dl_set(i)* tan(head_set(i) - proj_heading)) *...
(cos(heading_set(i) - proj_heading)^2)/(1 - proj_kappa * l_set(i)) + proj_kappa) *...
cos(heading_set(i) - proj_heading)/(1 - proj_kappa * l_set(i));
end
end
function [proj_x, proj_y,proj_heading, proj_kappa] = CalcProjPoint(s,frenet_path_x,frenet_path_y, frenet_path_heading,frenet_path_kappa,index2s)
%该函数将计算在frenet坐标系下,点(s,l)在frenet坐标轴的投影的直角坐标(proj_x,proj_y, proj_heading. proj_kappa)'
%先找匹配点的编号
match_index = 1;
while index2s (match_index)< s
match_index = match_index + 1;
end
match_point = [frenet_path_x(match_index) ;frenet_path_y(match_index)];
match_point_heading = frenet_path_heading(match_index) ;
match_point_kappa = frenet_path_kappa(match_index) ;
ds = s - index2s(match_index);
match_tor = [cos(match_point_heading) ;sin(match_point_heading)];
proj_point = match_point + ds * match_tor;
proj_heading = match_point_heading + ds * match_point_kappa;
proj_kappa = match_point_kappa;
proj_x = proj_point(1);
proj_y = proj_point(2);
end
这样就完成了从dp_path从动态规划里面出来,直到整个一条曲线把它采样完成以及转换成直角坐标系。
注意:dp_path_s_final理论上不需要自然坐标转直角坐标,因为后面还有个二次规划,动态规划毕竟是粗解,不是最优解,最终算法是动态规划出来再二次规划再转成直角坐标。还没讲到二次规划,所以暂时先用粗解转化生成path。
但是路径不完整,没有时间戳也没有速度。还是没法发给控制,所以有必要规划一个速度,然后从路径和速度合成轨迹,这才是控制所要的完整的轨迹。
下面写一个简单的速度规划,后面再细讲。直接把老王模型里面的复制过来用
最后发出去就完成了规划的流程,速度规划后面重新写一遍
把emplanner的输出作为决策规划模块的输出,然后再输入给控制
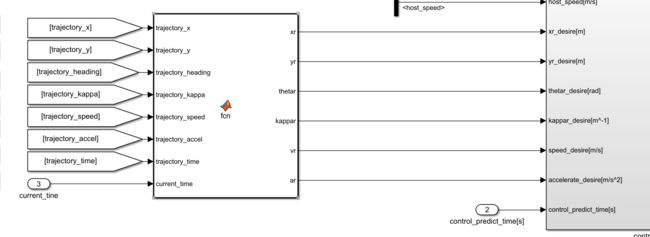
规划输出的不是一个一个点,而是一群轨迹的时候,控制也要改,现在去修改控制接口
解除注释,我们要先进行一些处理,新建一个函数
function [xr,yr,thetar,kappar,vr,ar] = fcn(trajectory_x,trajectory_y,trajectory_heading,...
trajectory_kappa,trajectory_speed,trajectory_accel,trajectory_time,current_time,ar)
%该函数根据规划的轨迹计算出期望跟踪的点
%由于控制也是有延迟,所以控制发出的期望跟踪的点是current_time + 0.01;
control_time = current_time + 0.01;
%规划发出的轨迹有一部分是拼接的,在刚启动的时候,stitch_time = -1,因此要先把它去掉
start_index = 1;
while (trajectory_time(start_index)== -1)
start_index = start_index + 1;
end
% 使用interp1插值计算得到xr yr thetar, kappar, vr, ar
% 由于interp1在端点会得到nan,因此需要防一手
% 解释,为什么需要trajectory_time(start_index) ~= 0
% 因为在刚启动时规划先执行(100ms),当规划完毕的时候控制已经执行了10次
% 那么在最开始的时候,规划还没给结果是控制已经执行了10次,在这10次中控制跟踪的轨迹是空轨迹
% simulink空轨迹表示为0,0,0,0,0,0.. .. . .,这样trajectory_time
% 也全是0,trajectory_time不单调递增
% 而interp1(x, y,x0) 要求x必须要单调递增,否则会报错
if control_time > trajectory_time (start_index) && trajectory_time(start_index)~= 0
xr = interp1(trajectory_time (start_index: end) , trajectory_x (start_index:end) , control_time);
yr = interp1(trajectory_time(start_index:end) , trajectory_y(start_index:end) , control_time);
thetar = interp1(trajectory_time(start_index:end), trajectory_heading(start_index:end), control_time) ;
kappar = interp1(trajectory_time(start_index: end) , trajectory_kappa(start_index:end) , control_time);
vr = interp1(trajectory_time(start_index:end), trajectory_speed(start_index:end) , control_time);
ar = interp1(trajectory_time(start_index:end), trajectory_accel(start_index : end) , control_time);
else
xr = trajectory_x(start_index);
yr = trajectory_y(start_index);
thetar = trajectory_heading(start_index);
kappar = trajectory_kappa(start_index);
vr = trajectory_speed(start_index);
ar = trajectory_accel(start_index) ;
end
在规划里,我们用-1来表示没有拼接轨迹
![]()
同时把planning_result的数据输入给控制
然后再把函数输出接给desire,让控制去跟踪
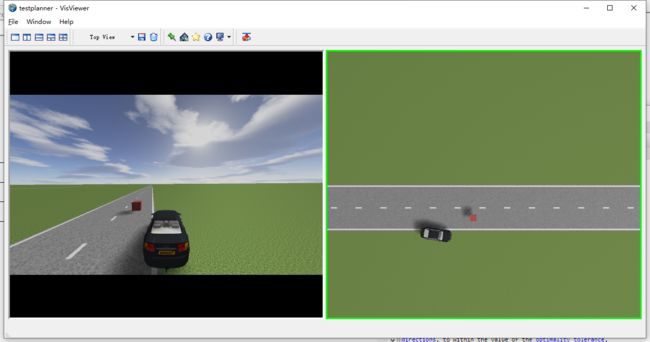
控制模块改好之后可以编译解决一下bug,点击运行,可以看到可以正常的避障(这里可以多放几个障碍物,更加直观)
发现车有点晃,改一下这里的列为4,sample_s为15,这样就不晃了
还是有点晃,但是好多了,后面二次规划再平滑
四、二次规划
1、轻决策与重决策
二次规划要求解空间是凸的,而动态规划开辟了凸空间
动态规划虽然叫规划,但是是做决策用的,如下图所示,动态规划算出一条粗解,粗解在哪个凸空间内,那么最终解就用它作为解空间(Apollo决策核心思想)
动态规划与决策的关系
决策算法分为重决策算法和轻决策算法,重决策算法基于人给定的规则,轻决策算法基于代价函数
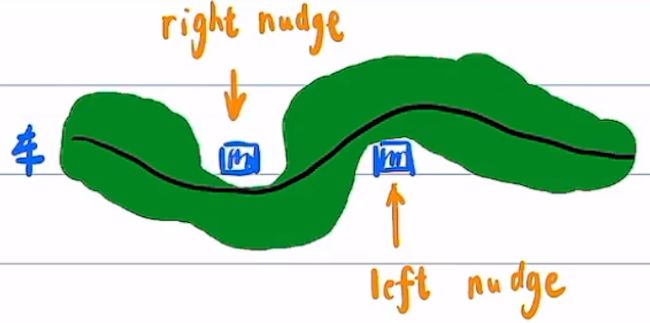
重决策:根据人给定的规则判断(综合与障碍物的距离,相对速度,周围环境信息)给出决策人事先写好场景与决策的映射关系
假设决策:right nudge(向右绕)
重决策优点:①计算量小;②在感知不强的情况下仍能做决策(融合了人的智慧)
缺点:①场景太多了,人无法完全覆盖
②人给出的决策所开辟的凸空间未必满足约束
轻决策算法:无先验规划,空间离散化,设计Cost function,动态规划算法求解离散空间的最优路径,该最优路径开辟凸空间
优点:①无人为规则, 可以处理复杂场景
②有粗解,通过设计代价函数,可以使粗解“满足”硬约束(无碰撞,最小曲率),这样使二次规划求解成功的机率大大增加(因为粗解在凸空间内部,所以该凸空间的“扭曲”程度至少有粗解兜底),大大缓解了基于人为规则的决策所造成的凸空间扭曲情况
缺点:①复杂场景计算量很大;②依赖预测(速度规划时会讲到);③要求周围环境全知(感知,定位要求高)④代价函数设计/最优解未必符合人的驾驶习惯
L2和高速L3主要用重决策,L4用轻决策算法
目前学术研究的热点是,轻决策和重决策结合的方向,博弈问题(Apollo 7.0的预测模块内加入)。还有就是深度学习做决策,规则来兜底的方法。
2、二次规划算法
二次规划算法比较简单,但是编程麻烦,细节多
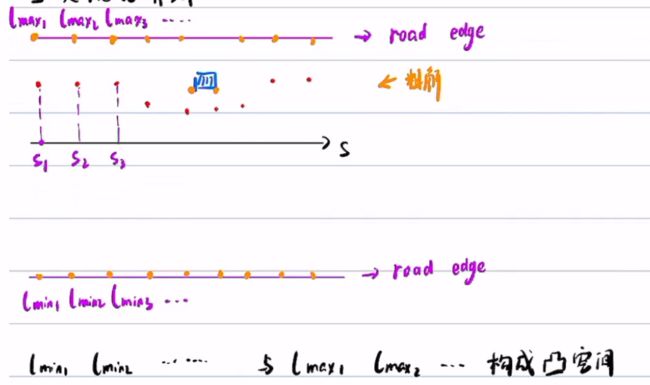
如图所示,红色点是动态规划出来的粗解,每个离散点si都有上下界[lmini,lmaxi],这些界限构成了凸空间
二次规划的求解空间就在此凸空间中搜索
已知
求![]() 满足:f(s)二阶导数连续
满足:f(s)二阶导数连续
f(s)尽可能平滑(f(s)的各阶导数的平方尽可能小)
Apollo3.5/5.0新增:f(s)尽可能在凸空间的中央
分段加加速度优化法
在![]() 与
与![]() 之间的曲线f(s)的四阶导数及以上皆为0
之间的曲线f(s)的四阶导数及以上皆为0
那么![]() ,
,![]() 可以进行有限项的泰勒展开(注意四阶及其后面都消掉了)
可以进行有限项的泰勒展开(注意四阶及其后面都消掉了)
写成矩阵形式:
如果要满足二阶导数连续要满足的等式约束
则分段加加速度约束为
记为![]() (等式约束)
(等式约束)
下面来看不等式约束,上面已经知道每个路径点的上下界
![]()
直接拿上下界来作为不等式约束
实际这样做并不准确,因为汽车不是质点,有体积,需要对汽车的四个角点做约束
注意这里的d1和d2并不是ab,是质心到汽车前后边界线的距离
然后得到四个角点
存在三角函数,非线性,不得不做一些近似处理:
这种近似是对安全性有利的,会将小车近似成大车
直接拿角点放到上下界来作为约束不合适,因为可能其他角点会碰到
做的保守一点
对于上届
对于下界
个人理解:碰撞检测算法不只一种,这个只是其中一种,还有基于膨胀圆碰撞等等方法
得到不等式约束及其矩阵形式
总的不等式约束为
记为![]() ,其中A为8n*3n,x为3n*1,b为8n*1
,其中A为8n*3n,x为3n*1,b为8n*1
代价函数Cost function
约束为
![]()
3、代码实践
首先需要继续修bug,
进入EM Planner的投影通用模块
主要改动为:增加全局变量pre_x_set,pre_y_set用来判断帧与帧之间的障碍物是否为同一个,帧与帧之间的物体的位置距离过大,认为是两个障碍物
function [match_point_index_set,proj_x_set, proj_y_set,proj_heading_set,proj_kappa_set] = ...
fcn(x_set,y_set,frenet_path_x,frenet_path_y,frenet_path_heading,frenet_path_kappa)
%该函数将批量计算x_set,y_set中的xy,在frenet_path下的投影的信息
%输入 x_set,y_set,待投影的点的集合
%x_set,y_set,frenet_path_x,frenet_path_y,frenet_path_heading,frenet_path_kappa
%曲线在直角坐标系下的x,y,heading,kappa
%输出:match_point_index_set 匹配点在frenet_path下的编号的集合(即从全局路径第一个点开始数,第几个点是匹配点)
% proj_x y heading kappa 投影的x,y,heading,kappa的集合
% 由于事先不知道x_set中到底有多少个点需要投影,因此事先声明一个最大的数量的点作为缓冲
n = 128;
% 并且由于不知道投影点的个数,所以也不知道输出的个数,因此输出也要做缓冲,用nan表示不存在的点
% 输出最多输出128个
% 输出初始化
match_point_index_set = ones(n,1) * nan;
proj_x_set = ones(n,1) * nan;
proj_y_set = ones(n,1) * nan;
proj_heading_set = ones(n,1) * nan;
proj_kappa_set = ones(n,1) * nan;
%找匹配点,需要利用上一个周期的结果作为下一个周期遍历的起点,因此需要声明两个全局变量
persistent is_first_run;
persistent pre_match_point_index_set;
persistent pre_frenet_path_x;
persistent pre_frenet_path_y;
persistent pre_frenet_path_heading;
persistent pre_frenet_path_kappa;
persistent pre_x_set;
persistent pre_y_set;
%算法主函数入口
if isempty(is_first_run)
%该if分支表示函数首次运行
is_first_run = 0;
pre_frenet_path_x = frenet_path_x;
pre_frenet_path_y = frenet_path_y;
pre_frenet_path_heading = frenet_path_heading;
pre_frenet_path_kappa = frenet_path_kappa;
%要记录首次运行计算的匹配点的结果供下个周期运行,先初始化
pre_match_point_index_set = ones(n,1) * nan;
%对x_set,y_set的点做遍历,找到他们的匹配点
for i = 1 : length(x_set)
if isnan(x_set(i))
break;
end
%首次运行时,没有任何提示,只能从frenet path的第一个点开始找
start_search_index = 1;
% 声明increase_count,用于表示在遍历时distance连续增加的个数
increase_count = 0;
% 开始遍历
min_distance = inf;
for j = start_search_index : length(frenet_path_x)
distance = (x_set(i) - frenet_path_x(j))^2 + (y_set(i) - frenet_path_y(j))^2;
if distance < min_distance
min_distance = distance;
match_point_index_set(i) = j;
increase_count = 0;
else
increase_count = increase_count + 1;
end
%如果distance连续增加50次就不要再遍历了,节省时间
if increase_count > 50
break;
end
end
%如何通过匹配点计算投影点,请参见《自动驾驶控制算法第七讲》
%或《自动驾驶决策规划算法》第一章第三节
%取出匹配点的编号
match_point_index = match_point_index_set(i);
%取出匹配点的信息
match_point_x = frenet_path_x(match_point_index);
match_point_y = frenet_path_y(match_point_index);
match_point_heading = frenet_path_heading(match_point_index);
match_point_kappa = frenet_path_kappa(match_point_index);
%计算匹配点的方向向量与法向量
vector_match_point = [match_point_x;match_point_y];
vector_match_point_direction = [cos(match_point_heading);sin(match_point_heading)];
%声明待投影点的位矢
vector_r = [x_set(i);y_set(i)];
%通过匹配点计算投影点
vector_d = vector_r - vector_match_point;
ds = vector_d' * vector_match_point_direction;
vector_proj_point = vector_match_point + ds * vector_match_point_direction;
proj_heading = match_point_heading + match_point_kappa * ds;
proj_kappa = match_point_kappa;
%计算结果输出
proj_x_set(i) = vector_proj_point(1);
proj_y_set(i) = vector_proj_point(2);
proj_heading_set(i) = proj_heading;
proj_kappa_set(i) = proj_kappa;
end
%匹配点的计算结果保存,供下一个周期使用
pre_match_point_index_set = match_point_index_set;
pre_x_set = x_set;
pre_y_set = y_set;
else
%此if分支表示不是首次运行
%对每个x_set上的点做处理
for i = 1 : length(x_set)
%不是首次运行,对于点x_set(i),y_set(i)来说,start_search_index =
%pre_match_point_index_set(i)
start_search_index = pre_match_point_index_set(i);%上个周期匹配点的编号作为本周期搜索的起点
% 声明increase_count,用于表示在遍历时distance连续增加的个数
%%%%%%%%%
%对于障碍物检测而言,当感知第一次检测到障碍物时,算法并不是首次运行,此时
%pre_match_point_index_set的值是nan,如果还用上一时刻的结果作为本周期搜索的起点
%必然会出问题,所以要修改
% 增加:判断帧与帧之间的障碍物是否为同一个
square_dis = (x_set(i) - pre_x_set(i))^2 + (y_set(i) - pre_y_set(i))^2;
if square_dis > 36
%帧与帧之间的物体的位置距离过大,认为是两个障碍物
start_search_index = nan;
end
% 声明increase_count_limit
increase_count_limit = 5;
if isnan(start_search_index)
%没有上个周期的结果,那就不能只检查5次了
increase_count_limit = 50;
%搜索起点也要设为1
start_search_index = 1;
end
increase_count = 0;
% 开始遍历
%这里多一个步骤,判断遍历的方向
%计算上个周期匹配点的位矢
vector_pre_match_point = [frenet_path_x(start_search_index);frenet_path_y(start_search_index)];
vector_pre_match_point_direction = ...
[cos(frenet_path_heading(start_search_index));sin(frenet_path_heading(start_search_index))];
%判断遍历的方向
flag = ([x_set(i);y_set(i)] - vector_pre_match_point)' * vector_pre_match_point_direction;
min_distance = inf;
if flag > 0.001
for j = start_search_index : length(frenet_path_x)
distance = (x_set(i) - frenet_path_x(j))^2 + (y_set(i) - frenet_path_y(j))^2;
if distance < min_distance
min_distance = distance;
match_point_index_set(i) = j;
increase_count = 0;
else
increase_count = increase_count + 1;
end
%如果distance连续增加increase_count_limit次就不要再遍历了,节省时间
if increase_count > increase_count_limit
break;
end
end
elseif flag < - 0.001
for j = start_search_index : -1 : 1
distance = (x_set(i) - frenet_path_x(j))^2 + (y_set(i) - frenet_path_y(j))^2;
if distance < min_distance
min_distance = distance;
match_point_index_set(i) = j;
increase_count = 0;
else
increase_count = increase_count + 1;
end
%如果distance连续增加increase_count_limit次就不要再遍历了,节省时间
if increase_count > increase_count_limit
break;
end
end
else
match_point_index_set(i) = start_search_index;
end
%如何通过匹配点计算投影点,请参见《自动驾驶控制算法第七讲》
%或《自动驾驶决策规划算法》第一章第三节
%取出匹配点的编号
match_point_index = match_point_index_set(i);
%取出匹配点的信息
match_point_x = frenet_path_x(match_point_index);
match_point_y = frenet_path_y(match_point_index);
match_point_heading = frenet_path_heading(match_point_index);
match_point_kappa = frenet_path_kappa(match_point_index);
%计算匹配点的方向向量与法向量
vector_match_point = [match_point_x;match_point_y];
vector_match_point_direction = [cos(match_point_heading);sin(match_point_heading)];
%声明待投影点的位矢
vector_r = [x_set(i);y_set(i)];
%通过匹配点计算投影点
vector_d = vector_r - vector_match_point;
ds = vector_d' * vector_match_point_direction;
vector_proj_point = vector_match_point + ds * vector_match_point_direction;
proj_heading = match_point_heading + match_point_kappa * ds;
proj_kappa = match_point_kappa;
%计算结果输出
proj_x_set(i) = vector_proj_point(1);
proj_y_set(i) = vector_proj_point(2);
proj_heading_set(i) = proj_heading;
proj_kappa_set(i) = proj_kappa;
end
%匹配点的计算结果保存,供下一个周期使用
pre_match_point_index_set = match_point_index_set;
pre_frenet_path_x = frenet_path_x;
pre_frenet_path_y = frenet_path_y;
pre_frenet_path_heading = frenet_path_heading;
pre_frenet_path_kappa = frenet_path_kappa;
pre_x_set = x_set;
pre_y_set = y_set;
end
EM Planner新建函数
function [l_min,l_max] = fcn(dp_path_s,dp_path_l,static_obs_s_set,static_obs_l_set,static_obs_length,static_obs_width)
% 该函数将输出每个离散的dp_path_s中的点s所对应的l的边界l_min, l_max
%输入动态规划的曲线dp_path_s dp_path_l
% 障碍物中心点的坐标static_obs_s_set,static_obs_l_set
% 障碍物的长宽static_obs_length,static_obs_width
% 输出l_min l_max l 的上下界
%注意一般真实障碍物投影到frenet后,长宽会变得扭曲,在这里近似用直角坐标的static_obs_length,static_gobs width的值代替frenet坐标下的值
%所以此em plannner不能处理参考线曲率过大的场景(r >= 200) Apollo的EM可以,但是需要大改,细节很多,这里暂时不做
%大曲率场景的避障,参考线模块,还有障碍物投影模块,速度规划模块要做很多特殊处理。
%输出初始化如果无障碍l的边界默认为±6
l_min = ones(60,1)*-6;
l_max = ones(60,1)*6;%对每个障碍物做遍历
for i = 1 : length(static_obs_s_set)
if isnan(static_obs_s_set(i))
break;
end
%计算障碍物尾部和头部的s
obs_s_min = static_obs_s(i) + static_obs_length/2;
obs_s_max = static_obs_s(i) - static_obs_length/2 ;
%找到obs_s_min,obs_s _max在dp_path_s 在 dp_path_s中的位置
start_index = FindNearIndex(dp_path_s,obs_s_min);
end_index = FindNearIndex(dp_path_s,obs_s_max);
%判断dp_path_l在障碍物的上面还是下面,(path在obs上面即决策为向左绕,否则为向右绕)
centre_index = FindNearIndex(dp_path_s,static_obs_s_set(i)) ;
if start_index ==1 && end_index == 1
% 障碍物已经完全在host的后面
continue;
end
path_l = dp_path_l(centre_index);
if path_l > static_obs_s_set(i)
%意味着决策是向左绕过障碍物
for j = start_index :end_index
% l_max(j)是所有决策为向左绕过障碍物的l边界的最大值
l_max(j) = min(l_max(j), static_obs_l_set(i) - static_obs_width/2);
end
else
%意味着决策是向右绕过障碍物
for j = start_index :end_index
% l_min(j)是所有决策为向左绕过障碍物的l边界的最大值
l_min(j) = max(l_min(j), static_obs_l_set(i) + static_obs_width/2);
end
end
end
end
function y = FindNearIndex(dp_path_s,obs_s)
%该函数将找到在dp path s上的所有点中,与obs_s最近的点,并返回该点在dp_path_s的编号
%这里要注意dp path s上的点是动态规划的结果,必然大于等于0,小于等于59
%而obs_s是障碍物在整个referenceline上的投影所得到的坐标,所以obs_s有可能小于0,也有可能大于59
if dp_path(1) >= obs_s
% 障碍物在车的后面
y = 1;
return;
elseif dp_path_s(end) < obs_s
% 障碍物在车的前面过远
y = 60;
return;
else
index = 1;
while dp_path_s(index) < obs_s
index = index + 1;
end
%循环退出的条件是dp_path_s(index) >= obs_s 判断一下index和 index-1到底哪个点离obs_s更近
if dp_path_s(index) - obs_s > obs_s - dp_path_s(index-1)
y = index - 1;
else
y = index;
end
end
end
这里障碍物长宽暂时用5和2
下面开始正式写二次规划算法
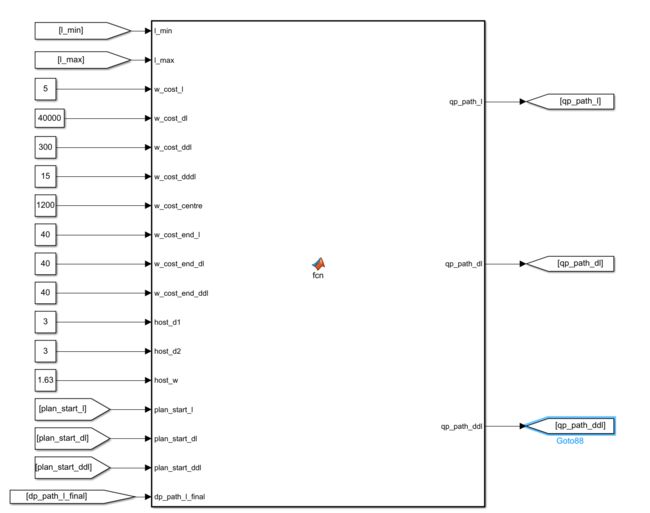
function [qp_path_l,qp_path_dl,qp_path_ddl] = ...
fcn(l_min,l_max,w_cost_l,w_cost_dl,w_cost_ddl,w_cost_dddl,w_cost_centre,w_cost_end_l,w_cost_end_dl,w_cost_end_ddl,...
host_d1,host_d2,host_w,...
plan_start_l,plan_start_dl,plan_start_ddl,dp_path_l_final)
% 路径二次规划
% 0.5*x'Hx + f'*x = min
% subject to A*x <= b
% Aeq*x = beq
% lb <= x <= ub;
% 输入:l_min l_max 点的凸空间
% w_cost_l 参考线代价
% w_cost_dl ddl dddl 光滑性代价
% w_cost_centre 凸空间中央代价
% w_cost_end_l dl dd1 终点的状态代价 (希望path的终点状态为(0,0,0))
% host_d1,d2 host质心到前后轴的距离
% host_w host的宽度
% plan_start_l,dl,ddl 规划起点
% 输出 qp_path_l dl ddl 二次规划输出的曲线
coder.extrinsic("quadprog");
% 待优化的变量的数量
n = 60;
% 输出初始化
qp_path_l = zeros(n,1);
qp_path_dl = zeros(n,1);
qp_path_ddl = zeros(n,1);
% H_L H_DL H_DDL H_DDDL Aeq beq A b 初始化
H_L = zeros(3*n, 3*n);
H_DL = zeros(3*n, 3*n);
H_DDL = zeros(3*n, 3*n);
H_DDDL = zeros(n-1, 3*n);
H_CENTRE = zeros(3*n, 3*n);
H_L_END = zeros(3*n, 3*n);
H_DL_END = zeros(3*n, 3*n);
H_DDL_END = zeros(3*n, 3*n);
Aeq = zeros(2*n-2, 3*n);
beq = zeros(2*n-2, 1);
A = zeros(8*n, 3*n);
b = zeros(8*n, 1);
% 期望的终点状态
end_l_desire = 0;
end_dl_desire = 0;
end_ddl_desire = 0;
% Aeq_sub
ds = 1;%纵向间隔
Aeq_sub = [1 ds ds^2/3 -1 0 ds^2/6;
0 1 ds/2 0 -1 ds/2];
% A_sub;
d1 = host_d1;
d2 = host_d2;
w = host_w;
A_sub = [1 d1 0;
1 d1 0;
1 -d2 0;
1 -d2 0;
-1 -d1 0;
-1 -d1 0;
-1 d2 0;
-1 d2 0];
% 生成Aeq
for i = 1:n-1
% 计算分块矩阵左上角的行和列
row = 2*i - 1;
col = 3*i - 2;
Aeq(row:row + 1,col:col + 5) = Aeq_sub;
end
% 生成A
for i = 1:n
row = 8*i - 7;
col = 3*i - 2;
A(row:row + 7,col:col + 2) = A_sub;
end
% 视频里用的找(s(i) - d2,s(i) + d1)的方法过于保守,在这里舍弃掉
% 只要找到四个角点所对应的l_min l_max 即可
% 。。。。。。。。。。。。。。
% [ . ]<-
% [ ]
% 。。。。。。。。。。。。。
front_index = ceil(d1/ds);
back_index = ceil(d2/ds); % ceil向上取整 ceil(3) = 3 ceil(3.1) = 4
% 生成b
for i = 1:n
% 左前 右前的index = min(i + front_index,60)
% 左后 右后的index = max(i - back_index,1)
index1 = min(i + front_index,n);
index2 = max(i - back_index,1);
b(8*i - 7:8*i,1) = [l_max(index1) - w/2;
l_max(index1) + w/2;
l_max(index2) - w/2;
l_max(index2) + w/2;
-l_min(index1) + w/2;
-l_min(index1) - w/2;
-l_min(index2) + w/2;
-l_min(index2) - w/2;];
end
%生成 lb ub 主要是对规划起点做约束
lb = ones(3*n,1)*-inf;
ub = ones(3*n,1)*inf;
lb(1) = plan_start_l;
lb(2) = plan_start_dl;
lb(3) = plan_start_ddl;
ub(1) = lb(1);
ub(2) = lb(2);
ub(3) = lb(3);
% for i = 2:n
% lb(3*i - 1) = - pi/8;
% ub(3*i - 1) = pi/8;
% lb(3*i) = -0.1;
% ub(3*i) = 0.1;
% end
% 生成H_L,H_DL,H_DDL,H_CENTRE
for i = 1:n
H_L(3*i - 2,3*i - 2) = 1;
H_DL(3*i - 1,3*i - 1) = 1;
H_DDL(3*i, 3*i) = 1;
end
H_CENTRE = H_L;
% 生成H_DDDL;
H_dddl_sub = [0 0 1 0 0 -1];
for i = 1:n-1
row = i;
col = 3*i - 2;
H_DDDL(row,col:col + 5) = H_dddl_sub;
end
% 生成H_L_END H_DL_END H_DDL_END
H_L_END(3*n - 2,3*n - 2) = 1;
H_DL_END(3*n - 1,3*n - 1) = 1;
H_DDL_END(3*n,3*n) = 1;
% 生成二次规划的H
H = w_cost_l * (H_L'*H_L) + w_cost_dl * (H_DL'*H_DL) + w_cost_ddl * (H_DDL'*H_DDL)...
+w_cost_dddl * (H_DDDL'*H_DDDL) + w_cost_centre * (H_CENTRE'*H_CENTRE) + w_cost_end_l * (H_L_END'*H_L_END)...
+w_cost_end_dl * (H_DL_END'* H_DL_END) + w_cost_ddl * (H_DDL_END'*H_DDL_END);
H = 2 * H;
% 生成f
f = zeros(3*n,1);
centre_line = 0.5 * (l_min + l_max);
centre_line = dp_path_l_final;
for i = 1:n
f(3*i - 2) = -2 * centre_line(i);
end
f = w_cost_centre * f;
% 终点要接近end_l dl ddl desire
f(3*n - 2) = f(3*n - 2) -2 * end_l_desire * w_cost_end_l;
f(3*n - 1) = f(3*n - 1) -2 * end_dl_desire * w_cost_end_dl;
f(3*n) = f(3*n) -2 * end_ddl_desire * w_cost_end_ddl;
X = quadprog(H,f,A,b,Aeq,beq,lb,ub);
% 这里没有对曲率做强制约束,并不好
% 可以用 |dl(i+1) - dl(i)|/ds <= kappa_max 近似去约束曲率
for i = 1:n
qp_path_l(i) = X(3*i - 2);
qp_path_dl(i) = X(3*i - 1);
qp_path_ddl(i) = X(3*i);
end
end
报错:
下面分析原因,新建可视化模块
function fcn(dp_s,dp_l,qp_l,l_min,l_max,obs_s_set,obs_l_set,start_s,start_l,start_dl)
coder.extrinsic("plot","axis","figure","drawnow","cla","fill");
obs_length = 5;
obs_width = 2;
host_l = 6;
host_w = 1.63;
cla;
host_p1_l = start_l + sin(atan(start_dl)) * host_l /2 + host_w/2 * cos(atan(start_dl));
host_p1_s = start_s + cos(atan(start_dl)) * host_l /2 - host_w/2 * sin(atan(start_dl));
host_p2_l = start_l + sin(atan(start_dl)) * host_l /2 - host_w/2 * cos(atan(start_dl));
host_p2_s = start_s + cos(atan(start_dl)) * host_l /2 + host_w/2 * sin(atan(start_dl));
host_p3_l = start_l - sin(atan(start_dl)) * host_l /2 + host_w/2 * cos(atan(start_dl));
host_p3_s = start_s - cos(atan(start_dl)) * host_l /2 - host_w/2 * sin(atan(start_dl));
host_p4_l = start_l - sin(atan(start_dl)) * host_l /2 - host_w/2 * cos(atan(start_dl));
host_p4_s = start_s - cos(atan(start_dl)) * host_l /2 + host_w/2 * sin(atan(start_dl));
host_area_x = [host_p1_s;host_p2_s;host_p4_s;host_p3_s];
host_area_y = [host_p1_l;host_p2_l;host_p4_l;host_p3_l];
fill(host_area_x,host_area_y,[0 1 1]);
hold on
plot(dp_s,dp_l,'r');
plot(dp_s,qp_l,'b');
plot(dp_s,l_min,dp_s,l_max);
axis([-8 70 -10 10]);
for i = 1:length(obs_s_set)
if isnan(obs_s_set(i))
break;
end
obs_p1_s = obs_s_set(i) + obs_length/2;
obs_p1_l = obs_l_set(i) + obs_width/2;
obs_p2_s = obs_s_set(i) + obs_length/2;
obs_p2_l = obs_l_set(i) - obs_width/2;
obs_p3_s = obs_s_set(i) - obs_length/2;
obs_p3_l = obs_l_set(i) + obs_width/2;
obs_p4_s = obs_s_set(i) - obs_length/2;
obs_p4_l = obs_l_set(i) - obs_width/2;
obs_area_s = [obs_p1_s;obs_p2_s;obs_p4_s;obs_p3_s];
obs_area_l = [obs_p1_l;obs_p2_l;obs_p4_l;obs_p3_l];
fill(obs_area_s,obs_area_l,[0 0 0]);
end
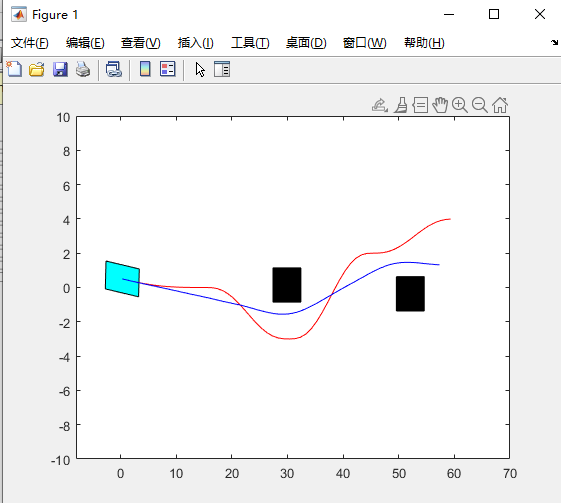
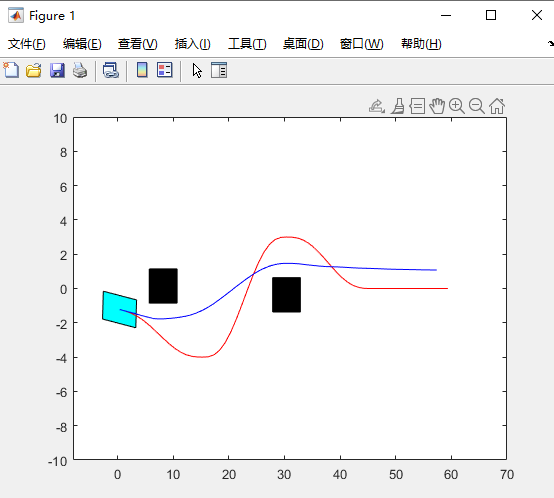
其中蓝色和红色线为上下界lmin,lmax,蓝色线为二次规划的轨迹线
把w_cost_dl调大
下面来看四个问题
①二次规划崩溃问题
②车控制不稳,抖动剧烈问题
③决策不稳定,朝令夕改问题
④速度规划如何影响路径规划
Q1:在靠近障碍物时,二次规划崩溃
根源在于:两个约束,碰撞约束和规划起点约束相互矛盾
规划起点要么是动力学递推要么是轨迹拼接而来,不能保证规划起点满足碰撞约束
使用拼接时,规划起点的约束与碰撞约束可能会发生矛盾
思考:为什么在无避障时不会崩溃
规划的线贴着边界
思考:为什么规划的路径会贴着边界
答:二次规划性质决定
带约束的二次规划的最小值只会在极小值或者边界点获得
下面来看避障问题
如果不带约束,极小值点就是中间的线
如果带约束,必然贴着约束边界
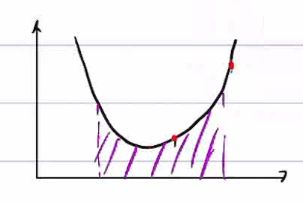
![]()
所以二次规划的曲线天然有往极小值靠拢的趋势,必然是贴着边界约束
实际有必要贴着边界吗,没必要。
所以采用以下改进:
①规划起点不管了,障碍物放大一点做安全缓冲
具体在代码上的做法就是改for循环
②改极小值点的位置
改下H
加上权重,把centre的权重调大
这样可以让车往中心跑
![]()
等于二分之一,
![]()
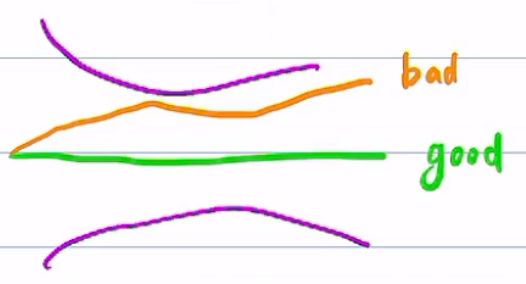
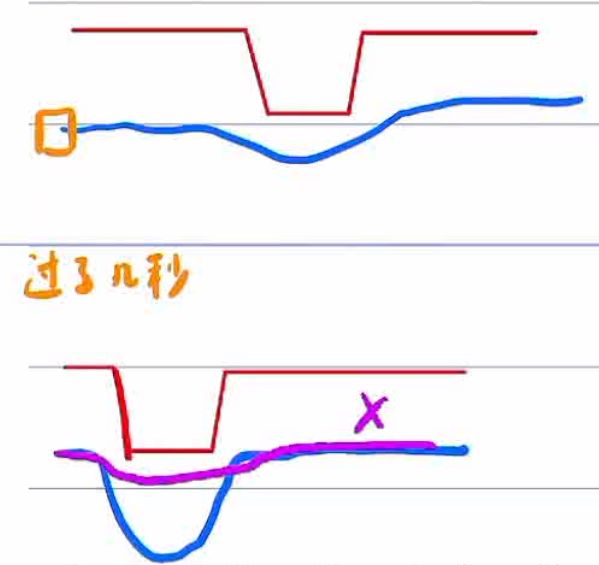
可以保证几何稳定,缺点是wcentre难调,调小了不起作用,调大了路径不平滑
如图所示,wcentre调大是棕色曲线,调小是紫色曲线
也就是说centre_line本来不是平滑曲线,如果调大就越接近centre_line导致其越来越不平滑
![]()
而这样做
![]()
优点就是,dp_path比上面那种平滑,曲线平滑相对好
缺点:dp_path几何不稳定
dp_path每一帧与每一帧得几何形状都会有巨大变化,若二次规划以dp_path作为centre line,qp path也会震荡
本身动态规划得解就会动来动去,而二次规划又是在趋近去它,所以自然也会动来动去
那么,到底该选择哪种呢?
老王推荐选择稳定的,防止晃来晃去,至于调参难可以和第二个问题一起解决
Q2:方向盘大幅摆动,车抖的厉害
根源:车规划的路径会天然往边界靠拢的趋势
解决:不允许反复横跳,加约束
![]()
新的问题:约束越多,求解越慢(反直觉)
![]()
因为约束越多,初值越难找
![]()
解决:削二次规划的规模,由60->20,二次规划求解完毕后在进行插值增密
最终Q1,Q2合起来的改进方案
①削qp规模,再插值增密
③规划起点不做约束
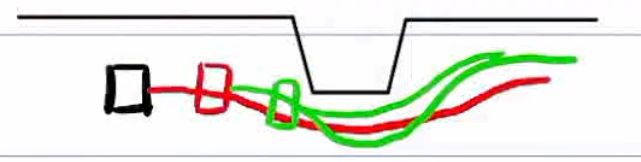
Q3:决策“朝令夕改”的问题
解决:Matlab里面暂时无解
Apollo里面使用打标签的方法:
上一帧
这一帧:只对无标签的obs作动态规划决策,若障碍物已有标签,直接沿用标签的决策
Matlab对结构体,字符串的支持有点弱,尽快切C++
Q4:速度规划对路径规划的影响
现在的规划path只处理静态障碍物,这样做有问题
这个case,速度规划无论怎么规划,都会碰撞(除非倒车)
怎么办呢?
已知上一帧的速度规划为10m/s匀速,上一帧的path为直线
这一帧
若path不考虑动态,则速度规划必无解
path规划要拿上一帧的轨迹去判断与动态障碍物的交互
上一帧的path + speed planning 会影响到这一帧的path planning
EM planner是SL planning与ST planing反复迭代的过程:
下面来到simulink进行改正
增加两个输入来限制dl和ddl
![]()
更新后的二次规划代码,增加了约束
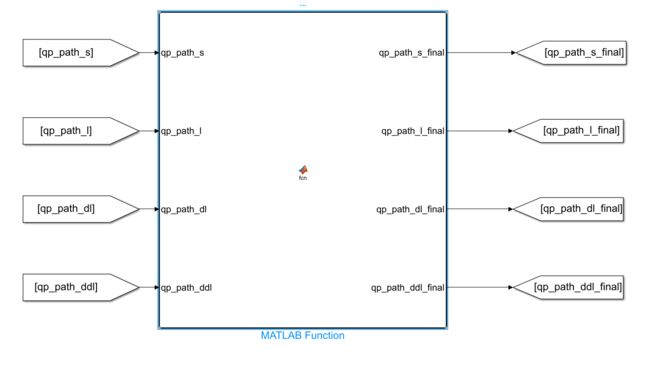
function [qp_path_s,qp_path_l,qp_path_dl,qp_path_ddl] = ...
fcn(l_min,l_max,w_cost_l,w_cost_dl,w_cost_ddl,w_cost_dddl,w_cost_centre,w_cost_end_l,w_cost_end_dl,w_cost_end_ddl,...
host_d1,host_d2,host_w,...
plan_start_s,plan_start_l,plan_start_dl,plan_start_ddl,...
delta_dl_max,delta_ddl_max)
% 路径二次规划
% 0.5*x'Hx + f'*x = min
% subject to A*x <= b
% Aeq*x = beq
% lb <= x <= ub;
% 输入:l_min l_max 点的凸空间
% w_cost_l 参考线代价
% w_cost_dl ddl dddl 光滑性代价
% w_cost_centre 凸空间中央代价
% w_cost_end_l dl dd1 终点的状态代价 (希望path的终点状态为(0,0,0))
% host_d1,d2 host质心到前后轴的距离
% host_w host的宽度
% plan_start_l,dl,ddl 规划起点
% 输出 qp_path_l dl ddl 二次规划输出的曲线
coder.extrinsic("quadprog");
% 待优化的变量的数量
n = 20;
% 输出初始化
qp_path_l = zeros(n,1);
qp_path_dl = zeros(n,1);
qp_path_ddl = zeros(n,1);
qp_path_s = zeros(n,1);
% H_L H_DL H_DDL H_DDDL Aeq beq A b 初始化
H_L = zeros(3*n, 3*n);
H_DL = zeros(3*n, 3*n);
H_DDL = zeros(3*n, 3*n);
H_DDDL = zeros(n-1, 3*n);
H_CENTRE = zeros(3*n, 3*n);
H_L_END = zeros(3*n, 3*n);
H_DL_END = zeros(3*n, 3*n);
H_DDL_END = zeros(3*n, 3*n);
Aeq = zeros(2*n-2, 3*n);
beq = zeros(2*n-2, 1);
A = zeros(8*n, 3*n);
b = zeros(8*n, 1);
% 更新:加入 dl(i+1) - dl(i) ddl(i+1) - ddl(i) 的约束
A_dl_minus = zeros(n - 1,3*n);
b_dl_minus = zeros(n - 1,1);
A_ddl_minus = zeros(n - 1,3*n);
b_ddl_minus = zeros(n - 1,1);
for i = 1:n-1
row = i;
col = 3*i - 2;
A_dl_minus(row,col:col+5) = [0 -1 0 0 1 0];
b_dl_minus(row) = delta_dl_max;
A_ddl_minus(row,col:col+5) = [0 0 -1 0 0 1];
b_ddl_minus(row) = delta_ddl_max;
end
% -max < a*x < max => ax < max && -ax < -(-max)
A_minus = [A_dl_minus;
-A_dl_minus;
A_ddl_minus;
-A_ddl_minus];
b_minus = [b_dl_minus;
b_dl_minus;
b_ddl_minus;
b_ddl_minus];
% 期望的终点状态
end_l_desire = 0;
end_dl_desire = 0;
end_ddl_desire = 0;
% Aeq_sub
ds = 3;%纵向间隔
for i = 1:n
qp_path_s(i) = plan_start_s + (i-1)*ds;
end
Aeq_sub = [1 ds ds^2/3 -1 0 ds^2/6;
0 1 ds/2 0 -1 ds/2];
% A_sub;
d1 = host_d1;
d2 = host_d2;
w = host_w;
A_sub = [1 d1 0;
1 d1 0;
1 -d2 0;
1 -d2 0;
-1 -d1 0;
-1 -d1 0;
-1 d2 0;
-1 d2 0];
% 生成Aeq
for i = 1:n-1
% 计算分块矩阵左上角的行和列
row = 2*i - 1;
col = 3*i - 2;
Aeq(row:row + 1,col:col + 5) = Aeq_sub;
end
% 生成A
for i = 2:n
row = 8*i - 7;
col = 3*i - 2;
A(row:row + 7,col:col + 2) = A_sub;
end
% 视频里用的找(s(i) - d2,s(i) + d1)的方法过于保守,在这里舍弃掉
% 只要找到四个角点所对应的l_min l_max 即可
% 。。。。。。。。。。。。。。
% [ . ]<-
% [ ]
% 。。。。。。。。。。。。。
front_index = ceil(d1/ds);
back_index = ceil(d2/ds); % ceil向上取整 ceil(3) = 3 ceil(3.1) = 4
% 生成b
for i = 2:n
% 左前 右前的index = min(i + front_index,60)
% 左后 右后的index = max(i - back_index,1)
% l_min l_max 都是60个点
index1 = min(3*i - 2 + front_index,n);
index2 = max(3*i - 2 - back_index,1);
b(8*i - 7:8*i,1) = [l_max(index1) - w/2;
l_max(index1) + w/2;
l_max(index2) - w/2;
l_max(index2) + w/2;
-l_min(index1) + w/2;
-l_min(index1) - w/2;
-l_min(index2) + w/2;
-l_min(index2) - w/2;];
end
%生成 lb ub 主要是对规划起点做约束
lb = ones(3*n,1)*-inf;
ub = ones(3*n,1)*inf;
lb(1) = plan_start_l;
lb(2) = plan_start_dl;
lb(3) = plan_start_ddl;
ub(1) = lb(1);
ub(2) = lb(2);
ub(3) = lb(3);
for i = 2:n
lb(3*i - 1) = - 2; %约束 l'
ub(3*i - 1) = 2;
lb(3*i) = -0.1; %约束 l''
ub(3*i) = 0.1;
end
% 生成H_L,H_DL,H_DDL,H_CENTRE
for i = 1:n
H_L(3*i - 2,3*i - 2) = 1;
H_DL(3*i - 1,3*i - 1) = 1;
H_DDL(3*i, 3*i) = 1;
end
H_CENTRE = H_L;
% 生成H_DDDL;
H_dddl_sub = [0 0 1 0 0 -1];
for i = 1:n-1
row = i;
col = 3*i - 2;
H_DDDL(row,col:col + 5) = H_dddl_sub;
end
% 生成H_L_END H_DL_END H_DDL_END
H_L_END(3*n - 2,3*n - 2) = 1;
H_DL_END(3*n - 1,3*n - 1) = 1;
H_DDL_END(3*n,3*n) = 1;
% 生成二次规划的H 因为ds != 1 所以 dddl = delta_ddl/ds;
H = w_cost_l * (H_L'*H_L) + w_cost_dl * (H_DL'*H_DL) + w_cost_ddl * (H_DDL'*H_DDL)...
+w_cost_dddl * (H_DDDL'*H_DDDL)/ds + w_cost_centre * (H_CENTRE'*H_CENTRE) + w_cost_end_l * (H_L_END'*H_L_END)...
+w_cost_end_dl * (H_DL_END'* H_DL_END) + w_cost_ddl * (H_DDL_END'*H_DDL_END);
H = 2 * H;
% 生成f
f = zeros(3*n,1);
centre_line = 0.5 * (l_min + l_max); % 此时centre line 还是60个点
% centre_line = dp_path_l_final;
for i = 1:n
f(3*i - 2) = -2 * centre_line(3*i - 2);
end
% 避免centreline权重过大影响轨迹平顺性
for i = 1:n
if abs(f(i)) > 0.3
f(i) = w_cost_centre * f(i);
end
end
% 终点要接近end_l dl ddl desire
f(3*n - 2) = f(3*n - 2) -2 * end_l_desire * w_cost_end_l;
f(3*n - 1) = f(3*n - 1) -2 * end_dl_desire * w_cost_end_dl;
f(3*n) = f(3*n) -2 * end_ddl_desire * w_cost_end_ddl;
X = quadprog(H,f,[A;A_minus],[b;b_minus],Aeq,beq,lb,ub);
for i = 1:n
qp_path_l(i) = X(3*i - 2);
qp_path_dl(i) = X(3*i - 1);
qp_path_ddl(i) = X(3*i);
end
end
增加一个函数来增密qp_path,因为我们已经知道导数,这里是精密插值,不是简单的插值
function [qp_path_s_final,qp_path_l_final, qp_path_dl_final,qp_path_ddl_final] = fcn(qp_path_s,qp_path_l,qp_path_dl,qp_path_ddl)
% 该函数将增密qp_path
n_init = 20;
% 增密的点的个数
n = 501;
% 输出初始化
qp_path_s_final = zeros(n,1);
qp_path_l_final = zeros(n,1);
qp_path_dl_final = zeros(n,1);
qp_path_ddl_final = zeros(n,1);
ds = (qp_path_s(end) - qp_path_s(1))/(n-1);
index = 1;
for i = 1:n
x = qp_path_s(1) + (i-1) * ds;
qp_path_s_final(i) = x;
while x >= qp_path_s(index)
index = index + 1;
if index == n_init
break;
end
end
% while 循环退出的条件是x
最后来到Frenet2Cartesian模块,更改输入
![]()
把里面的180改成600,一共500多个点
画图模块也更新一下
function fcn(dp_s,dp_l,qp_s,qp_l,l_min,l_max,obs_s_set,obs_l_set,start_s,start_l,start_dl)
coder.extrinsic("plot","axis","figure","drawnow","cla","fill");
obs_length = 5;
obs_width = 2;
host_l = 6;
host_w = 1.63;
cla;
host_p1_l = start_l + sin(atan(start_dl)) * host_l /2 + host_w/2 * cos(atan(start_dl));
host_p1_s = start_s + cos(atan(start_dl)) * host_l /2 - host_w/2 * sin(atan(start_dl));
host_p2_l = start_l + sin(atan(start_dl)) * host_l /2 - host_w/2 * cos(atan(start_dl));
host_p2_s = start_s + cos(atan(start_dl)) * host_l /2 + host_w/2 * sin(atan(start_dl));
host_p3_l = start_l - sin(atan(start_dl)) * host_l /2 + host_w/2 * cos(atan(start_dl));
host_p3_s = start_s - cos(atan(start_dl)) * host_l /2 - host_w/2 * sin(atan(start_dl));
host_p4_l = start_l - sin(atan(start_dl)) * host_l /2 - host_w/2 * cos(atan(start_dl));
host_p4_s = start_s - cos(atan(start_dl)) * host_l /2 + host_w/2 * sin(atan(start_dl));
host_area_x = [host_p1_s;host_p2_s;host_p4_s;host_p3_s];
host_area_y = [host_p1_l;host_p2_l;host_p4_l;host_p3_l];
fill(host_area_x,host_area_y,[0 1 1]);
hold on
plot(dp_s,dp_l,'r');
plot(qp_s,qp_l,'b');
plot(dp_s,l_min,dp_s,l_max);
axis([-8 70 -10 10]);
for i = 1:length(obs_s_set)
if isnan(obs_s_set(i))
break;
end
obs_p1_s = obs_s_set(i) + obs_length/2;
obs_p1_l = obs_l_set(i) + obs_width/2;
obs_p2_s = obs_s_set(i) + obs_length/2;
obs_p2_l = obs_l_set(i) - obs_width/2;
obs_p3_s = obs_s_set(i) - obs_length/2;
obs_p3_l = obs_l_set(i) + obs_width/2;
obs_p4_s = obs_s_set(i) - obs_length/2;
obs_p4_l = obs_l_set(i) - obs_width/2;
obs_area_s = [obs_p1_s;obs_p2_s;obs_p4_s;obs_p3_s];
obs_area_l = [obs_p1_l;obs_p2_l;obs_p4_l;obs_p3_l];
fill(obs_area_s,obs_area_l,[0 0 0]);
end
下面run一下看下效果
方向盘转角