蓝桥杯_Python B组_第五题_蜂巢 手写思路
前言:
我本来想看一下大家的第五题的解题思路,但是查了一圈发现好像现在网上没有这个相关的类型题,我就想着把我做这道题的思路分享一下,当然不一定对,我这个方法也比较玄学,期待大家在评论区讨论和更好的解法.
题目:试题 E: 蜂巢
时间限制 : 1.0s
内存限制 : 512.0MB
本题总分: 15 分
【问题描述】
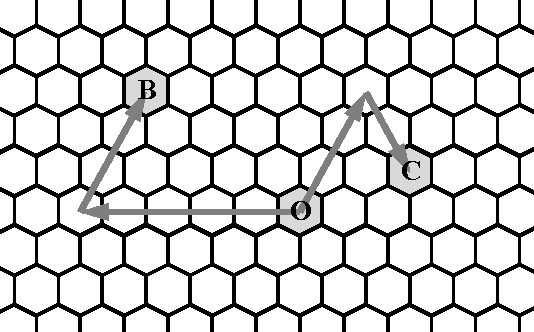
蜂巢由大量的六边形拼接而成,定义蜂巢中的方向为: 0 表示正西方向, 1
表示西偏北 60 ◦ , 2 表示东偏北 60 ◦ , 3 表示正东, 4 表示东偏南 60 ◦ , 5 表示西
偏南 60 ◦ 。
对于给定的一点 O ,我们以 O 为原点定义坐标系,如果一个点 A 由 O 点
先向 d 方向走 p 步再向 ( d + 2) mod 6 方向(
d 的顺时针 120 ◦ 方向)走 q 步到
达,则这个点的坐标定义为 ( d , p , q ) 。在蜂窝中,一个点的坐标可能有多种。
下图给出了点 B (0 , 5 , 3) 和点 C (2 , 3 , 2) 的示意。
给定点 ( d 1 , p 1 , q 1 ) 和点 ( d 2 , p 2 , q 2 ) ,请问他们之间最少走多少步可以到达?
【输入格式】
输入一行包含 6 个整数 d 1 , p 1 , q 1 , d 2 , p 2 , q 2 表示两个点的坐标,相邻两个整
数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示两点之间最少走多少步可以到达。
【样例输入】
0 5 3 2 3 2
【样例输出】
7
【评测用例规模与约定】
对于 25 % 的评测用例, p 1 , p 2 ≤ 10^ 3 ;
对于 50 % 的评测用例, p 1 , p 2 ≤ 10^ 5 ;
对于 75 % 的评测用例, p 1 , p 2 ≤ 10^ 7 ;
对于所有评测用例, 0 ≤ d 1 , d 2 ≤ 5 , 0 ≤ q 1 < p 1 ≤ 10^ 9 , 0 ≤ q 2 < p 2 ≤ 10^ 9。
思路:
我当时第一眼看过去觉得这是一个很明显的bfs题目吧,寻找一个最优值,然后我就去找其规律,我发现后面其实好像不用去队列遍历也可以做出来,我的思路是将每个点的值(d,p,q)转化为我们常见的(x,y)坐标.
具体的思路我大致写了一下,然后字比较丑不要在意,好久没手写了,我觉得整体思路应该是得当的,然后下面就是整体的代码:
import math
def x_y_transform(vertax):
d,p,q=vertax[0],vertax[1],vertax[2]
x=direction[d][0]*p+direction[(d+2)%6][0]*q
y=direction[d][1]*p+direction[(d+2)%6][1]*q
return (x,y)
def distance(a,b):
if a*b<0:
return abs(a)+abs(b)
else:
return abs(a-b)
a = math.sqrt(3)
direction=[[-1,0],[-0.5,a/2],[0.5,a/2],[1,0],[0.5,-a/2],[-0.5,-a/2]]
verlist=list(map(int,input().split()))
v1=verlist[:3]
v2=verlist[3:]
v1=x_y_transform(v1)
v2=x_y_transform(v2)
x_div=distance(v1[0],v2[0])
y_div=distance(v1[1],v2[1])
count=(2*y_div)//a
if x_div!=0:
x_div-=count*0.5
count+=x_div
print(int(count))
运行和测试也是正确的
中间坐标的显示转换也是想的那样
整体代码的空间复杂度和时间复杂度都是1,效率也很高,所以一个取巧的方法,不过还是担心有一些特殊情况没讨论到,我也不敢说这个就是对的,等后面官方发参考的代码吧