西瓜书第四章习题及答案

解答:
每个标记不同的数据特征向量都不相同,即树的每一条枝干(从根节点到叶子结点)就代表一种向量,这样的话决策树与训练集就是一致的了。
![]()
解答:
题目4.1中介绍了如果数据不含有冲突数据,那么就会产生绝对的过拟合现象,这也符合最小训练误差的准则,因此使用‘最小训练误差‘作为决策树划分选择准则的会产生在训练集上效果很好,而测试集上效果差的情况,即出现了过拟合现象。

分析:
表4.3属性数据值,有离散的有连续的,而基于信息熵进行属性划分只能是离散属性值,如果使用表4.3的数据集则需要对连续属性进行离散化-对应知识点-机器学习4.4连续与缺失值。
本实验采用去除表4.3中连续值的数据集西瓜数据集2.0。
解答:
第一部分-说在前面:
将数据集进行预处理(手动的 呜呜~ 要哭了!)
将离散的属性值进行数字化,将属性用英文代替
青绿-0 乌黑-1 浅白-2;
蜷缩 -0 稍蜷-1 硬挺-2
浊响-0 沉闷-1 清脆-2
清晰-0 稍糊-1 模糊-2
凹陷-0 稍凹-1 平坦-2
硬滑-0 软粘-1
是-1 否 -0
#texture 纹理 umbilical region---脐部
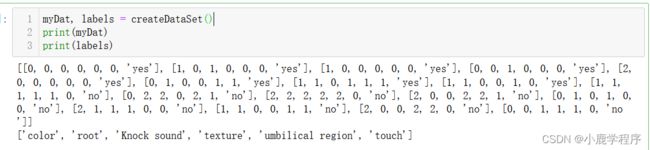
labels = ['color', 'root', 'Knock sound', 'texture','umbilical region','touch']
第二部分-计算机数据集的信息熵:
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt
第三部分-划分数据集
创建数据集函数:
from math import log
import operator
def createDataSet():
dataSet = [
[0, 0, 0, 0, 0, 0, 'yes'],
[1, 0, 1, 0, 0, 0, 'yes'],
[1, 0, 0, 0, 0, 0, 'yes'],
[0, 0, 1, 0, 0, 0, 'yes'],
[2, 0, 0, 0, 0, 0, 'yes'],
[0, 1, 0, 0, 1, 1, 'yes'],
[1, 1, 0, 1, 1, 1, 'yes'],
[1, 1, 0, 0, 1, 0, 'yes'],
[1, 1, 1, 1, 1, 0, 'no'],
[0, 2, 2, 0, 2, 1, 'no'],
[2, 2, 2, 2, 2, 0, 'no'],
[2, 0, 0, 2, 2, 1, 'no'],
[0, 1, 0, 1, 0, 0, 'no'],
[2, 1, 1, 1, 0, 0, 'no'],
[1, 1, 0, 0, 1, 1, 'no'],
[2, 0, 0, 2, 2, 0, 'no'],
[0, 0, 1, 1, 1, 0, 'no']
]
labels = ['color', 'root', 'Knock sound', 'texture','umbilical region','touch']
#change to discrete values
return dataSet, labels
按照给定特征划分数据集:
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] #chop out axis used for splitting
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
选择最好的数据集划分方式:
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #the last column is used for the labels
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(numFeatures): #iterate over all the features
featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
uniqueVals = set(featList) #get a set of unique values
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy #calculate the info gain; ie reduction in entropy
if (infoGain > bestInfoGain): #compare this to the best gain so far
bestInfoGain = infoGain #if better than current best, set to best
bestFeature = i
return bestFeature
第四部分-递归构建决策树
创建树的函数代码:
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]#stop splitting when all of the classes are equal
if len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSet
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:] #copy all of labels, so trees don't mess up existing labels
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
将结果输出展示:
myDat, labels = createDataSet()
print(myDat)
print(labels)
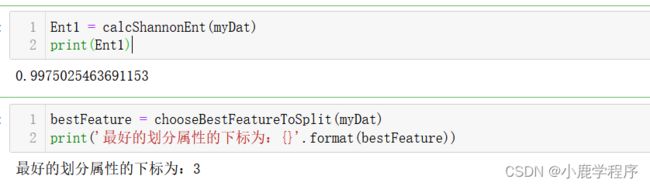
Ent1 = calcShannonEnt(myDat)
print(Ent1)
bestFeature = chooseBestFeatureToSplit(myDat)
print('最好的划分属性的下标为:{}'.format(bestFeature))
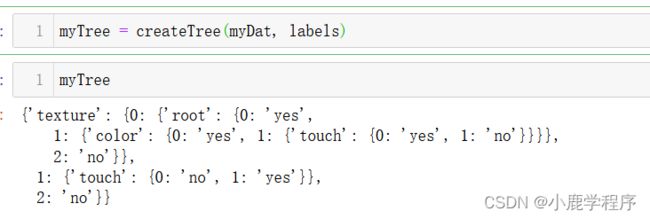
myTree = createTree(myDat, labels)
myTree
第五部分-使用matplotlib注解绘制树形图
使用文本注解绘制节点:
import matplotlib.pyplot as plt
#定义文本框和箭头的形式
decisionNode = dict(boxstyle = 'sawtooth', fc = '0.8')
leafNode = dict(boxstyle = 'round4', fc = '0.8')
arrow_args = dict(arrowstyle = '<-')
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy = parentPt, xycoords = 'axes fraction',\
xytext = centerPt, textcoords = 'axes fraction',\
va = 'center', ha ='center', bbox = nodeType, arrowprops = arrow_args)
def createPlot():
fig = plt.figure(1, facecolor='white')
fig.clf()
createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
plt.show()
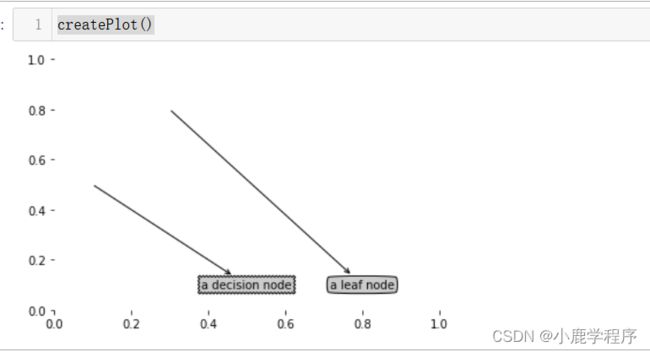
createPlot()#运行结果如下所示
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
获取树的层数:
#获取树的层数
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
创建retrieveTree函数输出预先存储的树信息,避免每次测试代码时都要从数据中创建树的麻烦。(就是保结果复制过来保存一下)
def retrieveTree(i):
listOfTrees =[{'texture': {0: {'root': {0: 'yes',
1: {'color': {0: 'yes', 1: {'touch': {0: 'yes', 1: 'no'}}}},
2: 'no'}},
1: {'touch': {0: 'no', 1: 'yes'}},
2: 'no'}},
{'texture': {0: {'root': {0: 'yes',
1: {'color': {0: 'yes', 1: {'touch': {0: 'yes', 1: 'no'}}}},
2: 'no'}},
1: {'touch': {0: 'no', 1: 'yes'}},
2: 'no'}}
]
return listOfTrees[i]
运行上述代码并查看结果:
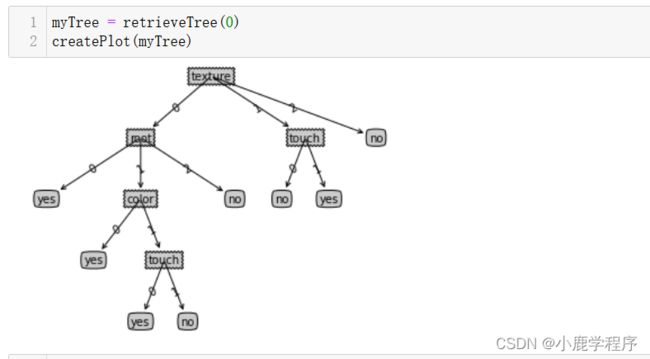
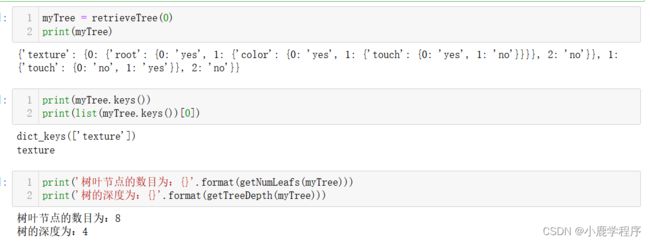
myTree = retrieveTree(0)
print(myTree)
print(myTree.keys())
print(list(myTree.keys())[0])
print('树叶节点的数目为:{}'.format(getNumLeafs(myTree)))
print('树的深度为:{}'.format(getTreeDepth(myTree)))
结果如下:
 plotTree函数-由三个函数构成,从下往上调用函数。
plotTree函数-由三个函数构成,从下往上调用函数。
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) #this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key],cntrPt,str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dict
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')###11111111
plt.show()
myTree = retrieveTree(0)
createPlot(myTree)
第六部分-说明
虽然输出的结果丑了点,也确实花费了不少时间(谁让我那么菜呐),所以有写的不好的地方还请各位大佬支出,大家共同进步哈。
今后如果有能力的话,会将最终的决策树美化一下,处理数据的文本样式而不是现在的0 1,再将连续型的属性值也加上去。
第七部分-参考书籍及文章
机器学习-西瓜书
机器学习实战-Peter Harrington