Python数据分析之探索性分析(多因子复合分析)
目录
一、假设检验:
二、交叉分析
1、分析属性与属性之间关系的方法
2、透视表
三、分组与钻取:
四、相关分析
1、相关系数分析
2、熵;条件熵;互信息(熵增益);增益率;基尼系数;
3、衡量离散数据的相关性
五、因子分析(成分分析)
1、主成分分析
2、具体案例HR的降维结果
六、线性回归分析
一、假设检验:
import numpy as np
import pandas as pd
import scipy.stats as ss
import seaborn as sns
import matplotlib.pyplot as plt
norm_dist=ss.norm.rvs(size=20)
#检测是不是正态分布
ss.normaltest(norm_dist) #基于偏度峰度的检验方法
ss.chi2_contingency([[15,95],[85,5]]) #卡方检验
#独立分布t检验
ss.ttest_ind(ss.norm.rvs(size=10),ss.norm.rvs(size=20))
ss.ttest_ind(ss.norm.rvs(size=100),ss.norm.rvs(size=200))
#方差分析(三因素)
ss.f_oneway([49,50,39,40,43],[28,32,30,26,34],[38,40,45,42,48])
结果:(返回对应的检验统计量取值及P值)
正态检验:
NormaltestResult(statistic=1.863200226764262, pvalue=0.39392288453069607)卡方检验:(检验统计量;P值;自由度;预期频率,基于表格的边际总和)
(126.08080808080808, 2.9521414005078985e-29, 1, array([[55., 55.], [45., 45.]]))独立t分布检验:
Ttest_indResult(statistic=0.37682239455779953, pvalue=0.7091463437965357) Ttest_indResult(statistic=1.1521645881654703, pvalue=0.25017689990448144)方差检验:
F_onewayResult(statistic=17.619417475728156, pvalue=0.0002687153079821641)
#QQ图
from statsmodels.graphics.api import qqplot
from matplotlib import pyplot as plt
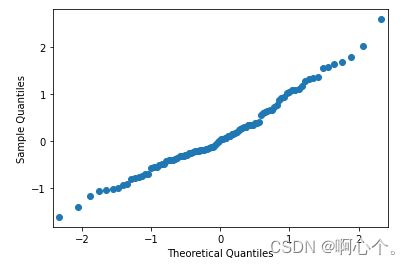
plt.show(qqplot(ss.norm.rvs(size=100)))QQ图——1.检验一列数据是否符合正态分布;2.检验两列数据是否符合同一分布
如何分析QQ图?
- 1.1 Q-Q散点图是沿着y=x分布时, 符合标准正态分布
- 1.2 Q-Q散点图沿y=ax+b分布时, 符合正态分布, 但非标准正态分布
二、交叉分析
1、分析属性与属性之间关系的方法
###交叉分析1——分析属性与属性之间关系的方法
df=pd.read_csv("D:/Users/DXX/Desktop/dxx.code/Python学习/HR_comma_sep.csv")
df=df.dropna(axis=0,how="any") #axis=0—行;how=“any”有一个空值删除;“all”全为空删除
df=df[df["last_evaluation"]<=1][df["salary"]!="nme"]
dp_indices=df.groupby(by="department").indices #department中各个属性的位置
sales_values=df["left"].iloc[dp_indices["sales"]].values #索引sales属性位置在left变量下的值
technical_values=df["left"].iloc[dp_indices["technical"]].values #索引technical属性位置在left变量下的值
##ttest_ind——对 2 个独立样本具有相同平均(预期)值的零假设的检验
ss.ttest_ind(sales_values,technical_values)
dp_keys=list(dp_indices.keys())
print(dp_keys)
dp_t_mat=np.zeros([len(dp_keys),len(dp_keys)])
for i in range(len(dp_keys)):
for j in range(len(dp_keys)):
p_value=ss.ttest_ind(df["left"].iloc[dp_indices[dp_keys[i]]].values,\
df["left"].iloc[dp_indices[dp_keys[j]]].values)[1]
dp_t_mat[i][j]=p_value
sns.heatmap(dp_t_mat,xticklabels=dp_keys,yticklabels=dp_keys) #热力图
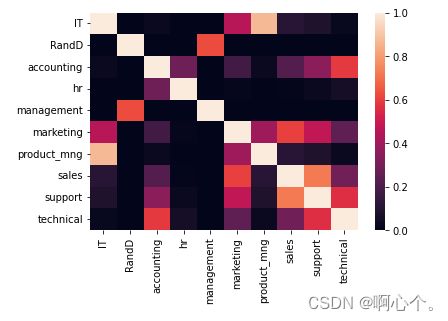
plt.show()ttest_ind()——对 2 个独立样本具有相同平均(预期)值的零假设的检验;
循环每两组属性进行独立t分布检验,将检验结果的P值绘成热力图,如下:
结果分析:P值大于给定显著性水平时,说明 2 个独立样本具有相同平均(预期)值的零假设成立。
2、透视表
#交叉分析2——透视表
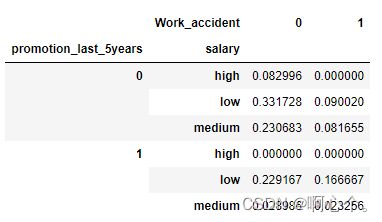
piv_tb=pd.pivot_table(df,values="left",index=["promotion_last_5years","salary"],\
columns=["Work_accident"],aggfunc=np.mean) #聚合函数aggfunc
piv_tb
#热力图
sns.set_context(font_scale=1.5)
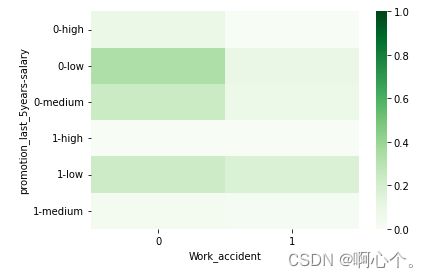
sns.heatmap(piv_tb,vmin=0,vmax=1,cmap=sns.color_palette("Greens",n_colors=256))
plt.show()
pivot_table()——透视表是一种可以对数据动态排布并且分类汇总的表格格式。
其中,aggfunc参数可以设置我们对数据聚合时进行的函数操作,默认为均值运算。
热力图可视化:
三、分组与钻取:
钻取是改变维的层次,变换分析的粒度——向上钻取;向下钻取
- 分隔(一阶差分)
- 拐点(二阶差分)
- 聚类方法分组
- 不纯度(Gini——基尼系数)
#分组与钻取
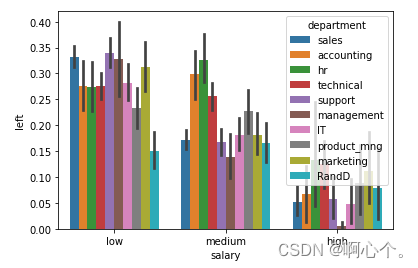
sns.barplot(x="salary",y="left",hue="department",data=df) #hue向下钻取
plt.show()向下钻取:分析部门之间在不同薪资水平下的离职率。
###连续属性数据离散化后才能分组
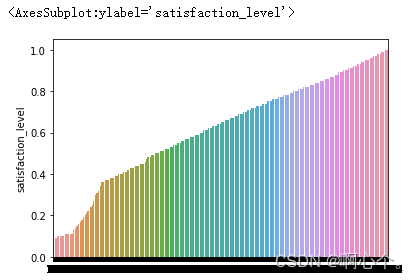
sl_s=df["satisfaction_level"]
sns.barplot(list(range(len(sl_s))),sl_s.sort_values()) 连续属性数据离散化后才能分组,可根据拐点来进行分组。
四、相关分析
1、相关系数分析
###相关系数分析
s1=pd.Series([0.1,0.2,1.1,2.4,1.3,0.3,0.5])
s2=pd.Series([0.5,0.4,1.2,2.5,1.1,0.7,0.1])
s1.corr(s2) #0.9333729600465924
s1.corr(s2,method="spearman") #0.7142857142857144
df=pd.DataFrame(np.array([s1,s2]).T)
df.corr(method="kendall")
# 0 1
# 0 1.00000 0.52381
# 1 0.52381 1.00000#相关分析
sns.heatmap(df.corr(),vmin=-1,vmax=1,cmap=sns.color_palette("Greens",n_colors=128))
plt.show()2、熵;条件熵;互信息(熵增益);增益率;基尼系数;
import pandas as pd
import numpy as np
import math
## 计算信息熵
def getEntropy(s):
# 找到各个不同取值出现的次数
if not isinstance(s, pd.core.series.Series):
s = pd.Series(s)
prt_ary = pd.Series.groupby(s , by = s).count().values / float(len(s))
return -(np.log2(prt_ary) * prt_ary).sum()
## 计算条件熵: 条件s1下s2的条件熵
def getCondEntropy(s1 , s2):
d = dict()
for i in list(range(len(s1))):
d[s1[i]] = d.get(s1[i] , []) + [s2[i]]
return sum([getEntropy(d[k]) * len(d[k]) / float(len(s1)) for k in d])
## 计算信息增益=信息熵-条件熵
def getEntropyGain(s1, s2):
return getEntropy(s2) - getCondEntropy(s1, s2)
## 计算增益率=信息增益/信息熵
def getEntropyGainRadio(s1, s2):
return getEntropyGain(s1, s2) / getEntropy(s2)
##计算概率平方和
def getProbSS(s):
if not isinstance(s, pd.core.series.Series):
s = pd.Series(s)
prt_ary = pd.Series.groupby(s, by = s).count().values / float(len(s))
return sum(prt_ary ** 2)
## 计算基尼系数
def getGini(s1, s2):
d = dict()
for i in list(range(len(s1))):
d[s1[i]] = d.get(s1[i] , []) + [s2[i]]
return 1-sum([getProbSS(d[k]) * len(d[k]) / float(len(s1)) for k in d])
s1 = pd.Series(['X1' , 'X1' , 'X2' , 'X2' , 'X2' , 'X2'])
s2 = pd.Series(['Y1' , 'Y1' , 'Y1' , 'Y2' , 'Y2' , 'Y2'])
print('CondEntropy(s1, s2):',getCondEntropy(s1, s2))
print('CondEntropy(s2, s1):',getCondEntropy(s2, s1))
print('EntropyGain(s1, s2):' , getEntropyGain(s1, s2))
print('EntropyGain(s2, s1):' , getEntropyGain(s2, s1))
print('EntropyGainRadio(s1, s2)' , getEntropyGainRadio(s1 , s2))
print('EntropyGainRadio(s2, s1)' , getEntropyGainRadio(s2 , s1))
print('Gini(s1, s2)' , getGini(s1, s2))
print('Gini(s2, s1)' , getGini(s2, s1))CondEntropy(s1, s2): 0.5408520829727552 CondEntropy(s2, s1): 0.4591479170272448 EntropyGain(s1, s2): 0.4591479170272448 EntropyGain(s2, s1): 0.4591479170272448 EntropyGainRadio(s1, s2) 0.4591479170272448 EntropyGainRadio(s2, s1) 0.5 Gini(s1, s2) 0.25 Gini(s2, s1) 0.2222222222222222s1和s2离散数据的相关系数结果分析:条件熵非对称;信息增益具有对称性;增益率非对称;基尼系数非对称
3、衡量离散数据的相关性
## 衡量离散值的相关性
import math
def getDiscreteCorr(s1, s2):
return getEntropyGain(s1,s2) / math.sqrt(getEntropy(s1) * getEntropy(s2))
############# 对离散型变量计算相关系数,并画出热力图, 返回相关性矩阵
def DiscreteCorr(C_data):
## 对离散型变量(C_data)进行相关系数的计算
C_data_column_names = C_data.columns.tolist()
## 存储C_data相关系数的矩阵
import numpy as np
dp_corr_mat = np.zeros([len(C_data_column_names) , len(C_data_column_names)])
for i in range(len(C_data_column_names)):
for j in range(len(C_data_column_names)):
# 计算两个属性之间的相关系数
temp_corr = getDiscreteCorr(C_data.iloc[:,i] , C_data.iloc[:,j])
dp_corr_mat[i][j] = temp_corr
# 画出相关系数图
fig = plt.figure()
fig.add_subplot(2,2,1)
sns.heatmap(dp_corr_mat ,vmin= - 1, vmax= 1, cmap= sns.color_palette('RdBu' , n_colors= 128) , xticklabels= C_data_column_names , yticklabels= C_data_column_names)
return pd.DataFrame(dp_corr_mat)
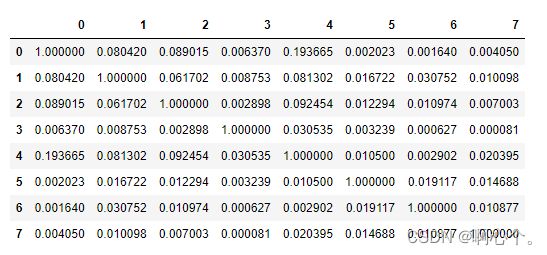
print('DiscreteCorr(s1, s2):' , getDiscreteCorr(s1, s2))
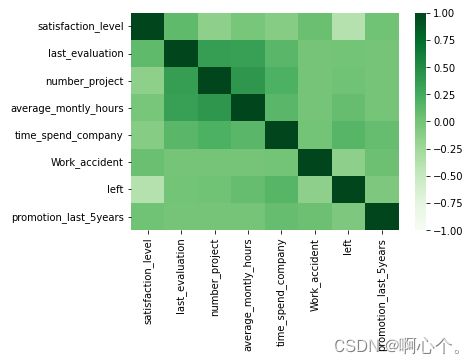
C_data=df.iloc[:2500,:]
DiscreteCorr(C_data)s1和s2离散数据的相关系数:
DiscreteCorr(s1, s2): 0.4791387674918639HR案例中离散数据(去除连续数据["satisfaction_level","last_evaluation"])的相关系数:
五、因子分析(成分分析)
1、主成分分析
data=np.array([np.array(np.random.random(10)*5),np.array(np.random.random(10))*2]).T
data
###调用PCA工具包
from sklearn.decomposition import PCA
lower_dim=PCA(n_components=1) #应用的是奇异值分解
lower_dim.fit(data)
print(lower_dim.explained_variance_ratio_) #方差贡献率0.87258255
lower_dim.fit_transform(data) #降维后的数据
###自定义PCA方法
def myPCA(data,n_components=100000):
mean_vals=np.mean(data,axis=0)
mid=data-mean_vals
cov_mat=np.cov(mid,rowvar=False)
from scipy import linalg
eig_vals,eig_vects=linalg.eig(np.mat(cov_mat))
eig_vals_index=np.argsort(eig_vals)
eig_vals_index=eig_vals_index[:-(n_components+1):-1]
eig_vects=eig_vects[:,eig_vals_index]
low_dim_mat=np.dot(mid,eig_vects)
return low_dim_mat,eig_vals,eig_vects
myPCA(data,n_components=1)
降维后的数据:
(array([[ 0.45178055],
[-0.60102064],
[ 2.07412265],
[ 2.24825295],
[-1.60803134],
[ 0.79006806],
[-2.16121735],
[-1.06061331],
[ 0.20482673],
[-0.3381683 ]]),
特征值:
array([2.12044475+0.j, 0.30963451+0.j]),
特征向量:
array([[ 0.99995422],
[-0.00956861]]))
2、具体案例HR的降维结果
from sklearn.decomposition import PCA
lower_dim=PCA(n_components=7) #应用的是奇异值分解
lower_dim.fit(df.drop(labels=["salary","department","left"],axis=1))
print(pd.DataFrame(lower_dim.explained_variance_ratio_)) #方差贡献率
#降维后的数据
lower_mat=lower_dim.fit_transform(df.drop(labels=["salary","department","left"],axis=1))
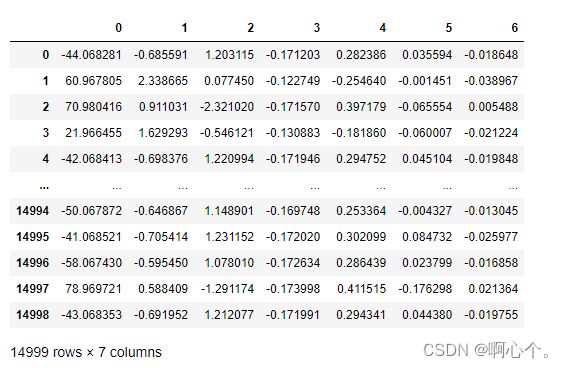
pd.DataFrame(lower_mat)
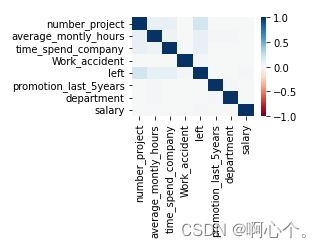
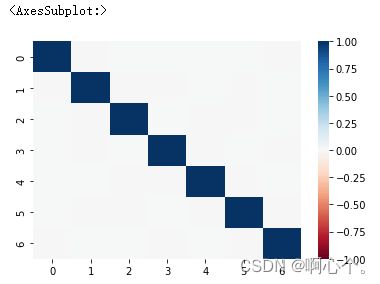
sns.heatmap(pd.DataFrame(lower_mat).corr(),vmin=-1,vmax=1,cmap=sns.color_palette("RdBu",n_colors=128))
降维后每个因子的方差贡献率:(一般选择累计方差贡献率大于80%的特征个数)
降维后的特征数据:(特征值*特征向量)
降维后特征之间的相关性分析:
(降维后的不同特征之间不具有相关性,能够反应样本数据之间的差异)
六、线性回归分析
x=np.arange(10).astype(np.float).reshape((10,1))
print(x)
y=x**2*3+4+np.random.random((10,1))
y
from sklearn.linear_model import LinearRegression
reg=LinearRegression()
res=reg.fit(x,y)
y_pred=res.predict(x)
print(res.coef_,res.intercept_)
y_pred
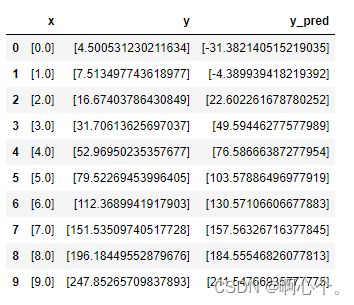
data=pd.DataFrame({'x':list(x),'y':list(y),'y_pred':list(y_pred)},index=np.arange(len(x)),columns=['x','y','y_pred'])
data
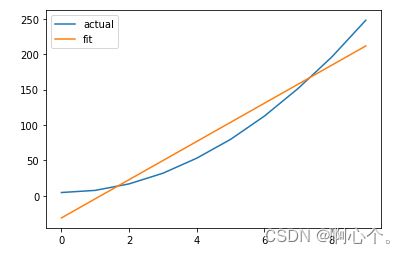
plt.plot(data["x"],data["y"])
plt.plot(data["x"],data["y_pred"])
plt.legend(["actual","fit"])
plt.show()原始数据及线性回归拟合值:
原始数据和拟合曲线对比图: