Python数据分析之机器学习：分类

目录

一、前期准备

二、划分数据集

三、引入分类的性能评价指标

四、分类算法概述

1、KNN（K-Nearest Neighbors）

2、朴素贝叶斯——朴素：特征间相互独立

3、决策树——切分标准以信息增益大的准则先进行决策

4、支持向量机（Support Vector Machine）

5、集成方法

5.1 袋装法（bagging）——并联

5.2 提升法（boosting）——串联

五、分类模型的训练及预测

---

一、前期准备

学习：通过接收到的数据，归纳提取出相同与不同之处。

机器学习：让计算机以数据为基础，进行归纳与总结。

• 监督学习：有标注——分类回归
• 非监督学习：无标注——聚类关联
• 半监督学习：部分有标注；部分无标注

案例数据及数据预处理和特征工程——

Python数据分析之特征工程-CSDN博客数据和特征决定了机器学习的上限，而模型和算法只是无限的逼近它而已。特征工程一般包括特征使用、特征获取、特征处理、特征监控四大方面。https://blog.csdn.net/weixin_45085051/article/details/126986556

---

二、划分数据集

1. 训练集：用来训练和拟合模型
2. 验证集：当通过训练集训练出多个模型后，使用验证集数据纠偏或者比较预测
3. 测试集：模型泛化能力的考量，泛化对未知数据的预测能力

k-fold交叉验证：将数据集分成k份，每次轮流做一遍测试集，其他做训练集

# 切分训练集和验证集(测试集)
from sklearn.model_selection import train_test_split
f_v = features.values  # 原先的数据是DataFrame,装换为数值，得到特征值
f_names = features.columns.values  # 得到特征名称
l_v = label.values
x_tt, x_validation, y_tt, y_validation = train_test_split(f_v, l_v, test_size=0.2)
# 将训练集再切分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x_tt, y_tt, test_size=0.25)

---

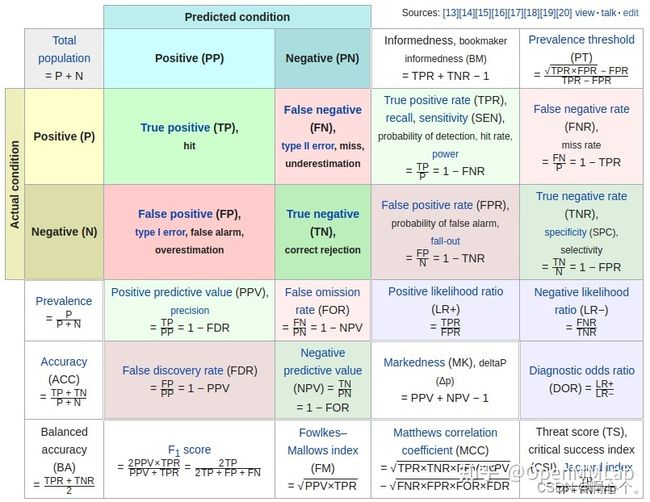
三、引入分类的性能评价指标

# 引入评价指标：精确度；召回率；F1分数
from sklearn.metrics import accuracy_score, recall_score, f1_score

准确率（Accuracy）

精确率（Precision）：在所有预测为正类的样本中，预测正确的比例，也称为查准率

召回率（Recall）：在所有实际为正类的样本中，预测正确的比例，也称为查全率

F1分数（F1 Score）：查准率和查全率的调和平均值

---

四、分类算法概述

1、KNN（K-Nearest Neighbors）

• 算法思想：找最近的K个邻居（最好奇数），K个邻居哪种类别多就判定为哪种类别
• 属于判别模型：不通过联合概率分布，直接可以获得输出对应最大分类的概率

2、朴素贝叶斯——朴素：特征间相互独立

• 连续值需要离散化，适合离散属性特征
• 拉普拉斯平滑：条件概率+1（防止分子为0）
• 属于生成模型：通过求输入与输出的联合概率分布，再求解类别归类的概率
• 两种分布：伯努利朴素贝叶斯——0-1分布；高斯朴素贝叶斯——高斯分布

3、决策树——切分标准以信息增益大的准则先进行决策

• 划分标准：信息增益（ID3）；信息增益率（C4.5）；Gini系数（CART）
• 过拟合采用剪枝策略：

1. 前剪枝在构造决策树以前规定好每个叶子节点有多少个样本或者规定决策树的最大深度
2. 后剪枝先构造出决策树，根据经验对样本值比较悬殊的节点进行修剪

4、支持向量机（Support Vector Machine）

• 算法思想：寻找一个可以最大限度地将两个样本的标注进行区分的超平面
• 为防止维度爆炸，先在低维空间计算，再进行扩维：

1. 核函数：线性核函数——没有用到核函数；
2. 多项式核函数——参数d确定扩充维度；
3. 高斯径向基RBF核函数——扩充到无限维，但可能过拟合

• 样本不平衡，出现少部分标注异常——引入松弛变量
• 多分类问题——两两排列组合进行二分类；某类与其它进行二分类 

5、集成方法

• 强可学习：多项式学习算法的效果较为明显
• 弱可学习：多项式学习算法的效果不很明显
• 算法思想：组合多个模型以获得更好的效果，将很多的机器学习算法组合在一起可能会得到比单一算法更好的计算结果，将几个弱可学习的分类器集合成强可学习的分类器的过程。

5.1 袋装法（bagging）——并联

• 流程：同时训练出几个相互独立的模型，用子模型对分类结果进行投票，对回归结果的参数取均值。
• 典型袋装法：随机森林（random forest）

1. 树的个数n_estimators；
2. 每棵数的特征数max_features；
3. 每棵树的训练集子集划分——设置准则要凸显每棵决策树的差异性
4. 优势：每个决策树可以并不使用全量特征；不需要剪枝，即可有效避免过拟合

5.2 提升法（boosting）——串联

• 流程：下一个模型用上一个模型的预测结果进行训练，多个模型级联，最后加权叠加，得到判决结果。
• 典型提升法：Adaboost

1. 不考虑复杂度，其精度高，且灵活可调；
2. 几乎不用担心过拟合；
3. 简化特征工程的流程

---

五、分类模型的训练及预测结果

# 引入划分数据集的方式
from sklearn.model_selection import train_test_split
# 引入评价指标
from sklearn.metrics import accuracy_score, recall_score, f1_score
# 引入分类模型
from sklearn.neighbors import NearestNeighbors,KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB,BernoulliNB  #高斯贝叶斯，伯努利贝叶斯
from sklearn.tree import DecisionTreeClassifier,export_graphviz  #决策树及画树
from sklearn.svm import SVC  # 从SVM中引入SVC分类器
from sklearn.ensemble import RandomForestClassifier  # 随机森林-bagging集成方法
from sklearn.ensemble import AdaBoostClassifier  # AdaBoost-boosting集成方法


def hr_modeling(features, label):
# 切分训练集和验证集(测试集)
    f_v = features.values  # 原先的数据是DataFrame,装换为数值，得到特征值
    f_names = features.columns.values  # 得到特征名称
    l_v = label.values
    x_tt, x_validation, y_tt, y_validation = train_test_split(f_v, l_v, test_size=0.2)
# 将训练集再切分为训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x_tt, y_tt, test_size=0.25)

#将模型的名字和模型函数作为元组添加到列表当中存储；
    models = []
    models.append(("KNN",KNeighborsClassifier(n_neighbors=3))) #指定邻居个数
    models.append(("GaussianNB",GaussianNB()))  #高斯贝叶斯
    models.append(("BernoulliNB",BernoulliNB()))  #伯努利贝叶斯
    models.append(("DecisionTreeGini",DecisionTreeClassifier(min_impurity_split=0.1)))
    #默认criterion是基尼系数，可以填参数来剪枝，进行最小不纯度切分

    models.append(("DecisionTreeEntropy",DecisionTreeClassifier(criterion="entropy")))
    #信息增益

    models.append(("SVM Classifier",SVC(C=1000)))  
    #可以通过参数C来控制精度，C越大要求精度越高；  C——错分点的惩罚度

    models.append(("RandomForest",RandomForestClassifier()))  #可以添加参数调整
    # n_estimators决策树的个数
    # max_features=None表示每棵决策树取全局特征；
    # bootstrap=True有放回采样；False无放回采样
    # oob_score=True将没有被选择到的样本作为验证集

   models.append(("Adaboost",AdaBoostClassifier(base_estimator=SVC(),algorithm='SAMME')))
    # base_estimator 弱基础分类器，需要具备两个属性：classes_ and n_classes_
    # n_estimators 级联的分类器数量
    # learning_rate 权值衰减率
    # algorithm 如果base_estimator能得到分类的概率值——'SAMME.R'

#循环调用所有模型进行训练、预测
    for clf_name, clf in models:
        clf.fit(x_train, y_train)
        xy_lst = [(x_train, y_train), (x_validation, y_validation), (x_test, y_test)]
        for i in range(len(xy_lst)):
            x_part = xy_lst[i][0]  # 为遍历中的第0部分
            y_part = xy_lst[i][1]  # 为遍历中的第1部分
            y_pred = clf.predict(x_part)
            print(i)  # i是下标，0表示训练集，1表示验证集，2表示测试集
            print(clf_name, "ACC:", accuracy_score(y_part, y_pred))
            print(clf_name, "REC:", recall_score(y_part, y_pred))
            print(clf_name, "F-score:", f1_score(y_part, y_pred))

# 调用所有模型
def main():
    features, label = hr_preprocessing()  # 默认是False,也可以改为True
    hr_modeling(features, label)

if __name__ == "__main__":
    main()

KNN的预测结果：

0训练集
KNN ACC: 0.975108345371708
KNN REC: 0.9596287703016241
KNN F-score: 0.9486238532110092
1验证集
KNN ACC: 0.959
KNN REC: 0.9314868804664723
KNN F-score: 0.9122055674518201
2测试集
KNN ACC: 0.954
KNN REC: 0.9273972602739726
KNN F-score: 0.9075067024128687

高斯贝叶斯的训练结果：

0
GaussianNB ACC: 0.7848649849983331
GaussianNB REC: 0.7614849187935034
GaussianNB F-score: 0.628976619394404
1
GaussianNB ACC: 0.7893333333333333
GaussianNB REC: 0.7842565597667639
GaussianNB F-score: 0.629976580796253
2
GaussianNB ACC: 0.779
GaussianNB REC: 0.7753424657534247
GaussianNB F-score: 0.630640668523677

伯努利贝叶斯的训练结果：

0
BernoulliNB ACC: 0.8400933437048561
BernoulliNB REC: 0.46635730858468677
BernoulliNB F-score: 0.5827776167004929
1
BernoulliNB ACC: 0.8493333333333334
BernoulliNB REC: 0.48833819241982507
BernoulliNB F-score: 0.5971479500891266
2
BernoulliNB ACC: 0.8386666666666667
BernoulliNB REC: 0.45616438356164385
BernoulliNB F-score: 0.5791304347826087

基于基尼系数划分决策树的训练结果：

0
DecisionTreeGini ACC: 0.8169796644071563
DecisionTreeGini REC: 0.694199535962877
DecisionTreeGini F-score: 0.6449665876266436
1
DecisionTreeGini ACC: 0.82
DecisionTreeGini REC: 0.7376093294460642
DecisionTreeGini F-score: 0.652061855670103
2
DecisionTreeGini ACC: 0.8316666666666667
DecisionTreeGini REC: 0.7246575342465753
DecisionTreeGini F-score: 0.6769033909149073

基于信息增益决策树的训练结果：

0
DecisionTreeEntropy ACC: 1.0
DecisionTreeEntropy REC: 1.0
DecisionTreeEntropy F-score: 1.0
1
DecisionTreeEntropy ACC: 0.9746666666666667
DecisionTreeEntropy REC: 0.9723032069970845
DecisionTreeEntropy F-score: 0.9460992907801418
2
DecisionTreeEntropy ACC: 0.9753333333333334
DecisionTreeEntropy REC: 0.9684931506849315
DecisionTreeEntropy F-score: 0.950268817204301

支持向量机分类模型的训练结果：0
SVM Classifier ACC: 0.9852205800644516
SVM Classifier REC: 0.9549883990719258
SVM Classifier F-score: 0.9686985172981878
1
SVM Classifier ACC: 0.9736666666666667
SVM Classifier REC: 0.9387755102040817
SVM Classifier F-score: 0.942209217264082
2
SVM Classifier ACC: 0.9683333333333334
SVM Classifier REC: 0.9356164383561644
SVM Classifier F-score: 0.9349760438056125

随机森林的训练结果：

0
RandomForest ACC: 1.0
RandomForest REC: 1.0
RandomForest F-score: 1.0
1
RandomForest ACC: 0.9896666666666667
RandomForest REC: 0.9664723032069971
RandomForest F-score: 0.9771554900515843
2
RandomForest ACC: 0.9896666666666667
RandomForest REC: 0.9657534246575342
RandomForest F-score: 0.9784871616932685

Adaboost 算法的训练结果：

0
Adaboost ACC: 0.7605289476608512
Adaboost REC: 0.0
Adaboost F-score: 0.0
1
Adaboost ACC: 0.7713333333333333
Adaboost REC: 0.0
Adaboost F-score: 0.0
2
Adaboost ACC: 0.7566666666666667
Adaboost REC: 0.0
Adaboost F-score: 0.0