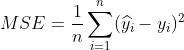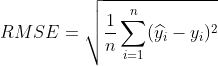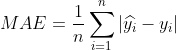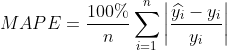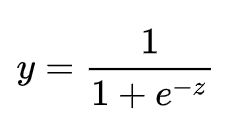Python数据分析之机器学习：回归

目录

一、前情回顾

二、 回归的评价指标

三、回归算法概述

1、线性回归——最小二乘法求解回归系数 

2、进化线性回归——正则化（抑制过拟合） 

2.1 L2范数正则化（Ridge Regression，岭回归 ）

2.2  L1范数正则化（LASSO，Least Absoulute Shrinkage and Selection Operator，最小绝对收缩选择算子）

2.3 L1正则项和L2正则项结合（弹性网络）

3、逻辑斯特回归(Logistic Regression)

4、人工神经网络（ANN）

4.1 训练网络基本过程

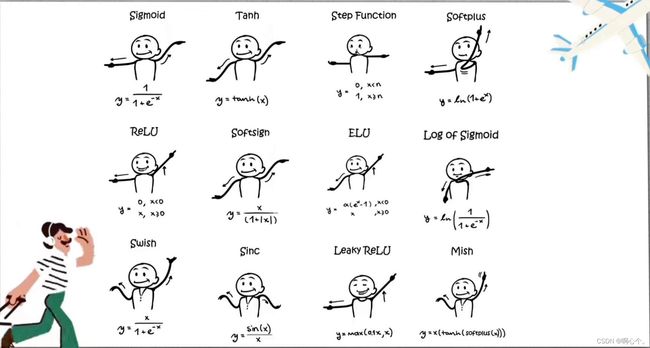
 4.2 一些激活函数

4.3 损失函数（代价函数）

4.4 梯度下降算法—适中的学习率：下山的步长

4.5 更优的下山方法：（优化器的升级）

4.6 改善预测精度的问题：

5、 决策树——回归树

5.1 算法思想：

5.2 简单回归树案例：

四、回归模型的训练及预测结果

---

一、前情回顾

Python数据分析之机器学习：分类_啊心个。的博客-CSDN博客机器学习的分类模型包括：k近邻算法，朴素贝叶斯，决策树，支持向量机，集成算法（随机森林、Adaboost）https://blog.csdn.net/weixin_45085051/article/details/127145472?spm=1001.2014.3001.5502#:~:text=%E5%8F%91%E5%B8%83-,Python%E6%95%B0%E6%8D%AE%E5%88%86%E6%9E%90%E4%B9%8B%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%EF%BC%9A%E5%88%86%E7%B1%BB,-%E5%95%8A%E5%BF%83%E4%B8%AA

---

二、 回归的评价指标

均方误差（Mean Square Error）

均方根误差（Root Mean Square Error）

平均绝对误差（Mean Absolute Error）

平均绝对百分比误差（Mean Absolute Percentage Error）

其中，当因变量取值有0时，平均绝对百分比误差不适用。

#引入回归评价指标
from sklearn import metrics
MSE = metrics.mean_squared_error(y_part, y_pred)
RMSE = metrics.mean_squared_error(y_part, y_pred) ** 0.5
MAE = metrics.mean_absolute_error(y_part, y_pred)
MAPE = metrics.mean_absolute_percentage_error(y_part, y_pred)

---

三、回归算法概述

1、线性回归——最小二乘法求解回归系数 

 代价函数：

2、进化线性回归——正则化（抑制过拟合） 

2.1 L2范数正则化（Ridge Regression，岭回归 ）

2.2  L1范数正则化（LASSO，Least Absoulute Shrinkage and Selection Operator，最小绝对收缩选择算子）

2.3 L1正则项和L2正则项结合（弹性网络）

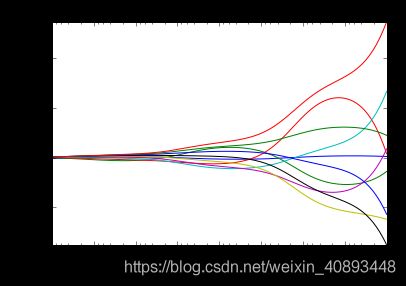
正则化惩罚项和权重系数的关系：

正则化力度alpha越大，权重系数越小；正则化力度alpha越大，权重系数越小。

基于以上回归模型的代价函数发现：alpha越大，那么正则项惩罚的就越厉害，得到回归系数w就越小，最终趋近与0。而如果alpha越小，即正则化项越小，那么回归系数w就越来越接近于普通的线性回归系数，即正则项惩罚系数太小了，和没惩罚一样，回归系数和惩罚后的回归系数几乎一样。

3、逻辑斯特回归(Logistic Regression)

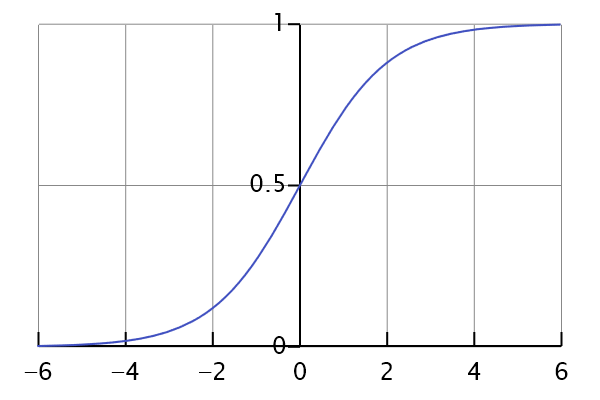
引入Sigmoid函数，通常用于解决二分类问题，也可作为激活函数应用于神经网络：

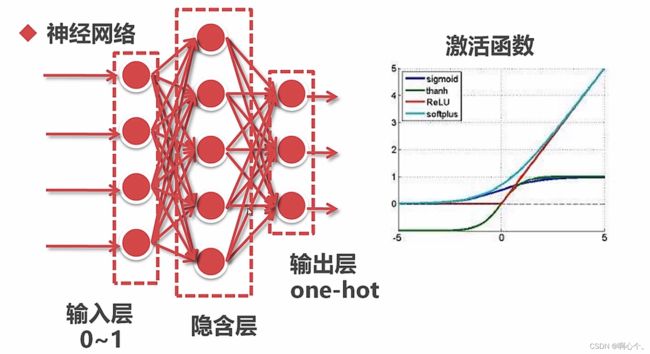
4、人工神经网络（ANN）

• 神经网络是一个正向求解的过程，通过不断反向迭代来接近理想解的过程。
• 基本要素：输入层；隐含层；输出层；激活函数；损失函数；梯度下降算法；反向传播

4.1 训练网络基本过程：

遍历每一个样本点，计算输出每个样本点的结果（权重和偏置），向前传播，计算误差和梯度值；反向传播，梯度下降法更新模型（链式法则）

1. 初始化权重
2. 根据权重计算结果
3. 计算误差
4. 根据误差反向传播调整权重
5. 重复以上步骤n次，直到达到一定条件

 4.2 一些激活函数：

4.3 损失函数（代价函数）

数据损失+正则化惩罚项——优化损失函数最小

4.4 梯度下降算法—适中的学习率：下山的步长

• BGD批量梯度下降：容易得到全局最优解，但是由于每次考虑所有样本，速度很慢
• SGD随机梯度下降：每次找一个样本，迭代速度快，但不一定每次都朝着收敛的方向
• MBGD小批量梯度下降法：每次更新选择一小部分数据来算（minibatchsize）

4.5 更优的下山方法：（优化器的升级）

• AdaGrad——动态学习率（经常更新的参数学习率更小，不经常更新的参数学习率更大，存在的问题是频繁更新的参数的学习率可能过小以至于消失）
• RMSProp——优化动态学习率
• AdaDelta——无需设置学习率
• Adam——融合AdaGrad和RMSProp
• Momentum——模拟动量（考虑惯性）

4.6 改善预测精度的问题：

1. 权重和偏置参数要初始化，即随机给定一种参数初值
2. 数据的预处理：归一化，标准化（无量纲化）
3. 易受到离群点的影响，易过拟合——正则化，dropout
4. 激活函数（非线性变换）将数据限定在一定范围内
5. 输出结果进行softmax转化——归一化的概率

5、 决策树——回归树

主流的决策树算法：

算法	适用模型		树结构	特征选择		连续值处理	缺失值处理	剪枝
ID3	分类		多叉树	信息增益最大		不支持	不支持	不支持
C4.5	分类		多叉树	信息增益率最大		支持	支持	支持
CART	分类	回归	二叉树	基尼系数最小	均方差	支持	支持	支持

其中：CART树全称Classification And Regression Tree，即可以用于分类，也可以用于回归，这里指的回归树就是CART树，ID3和C4.5不能用于回归问题。

5.1 算法思想：

1、将整个输入空间划分为多个子区域：

• 回归树采用的是自顶向下的贪婪式递归方案，即每一次的划分，只考虑当前最优，而不回头考虑之前的划分。
• 连续值切分原则——按照最小均方差切分，保证叶子节点均方差和RSS最小，公式如下：

2、每个子区域输出的为该区域内所有训练样本的平均值；

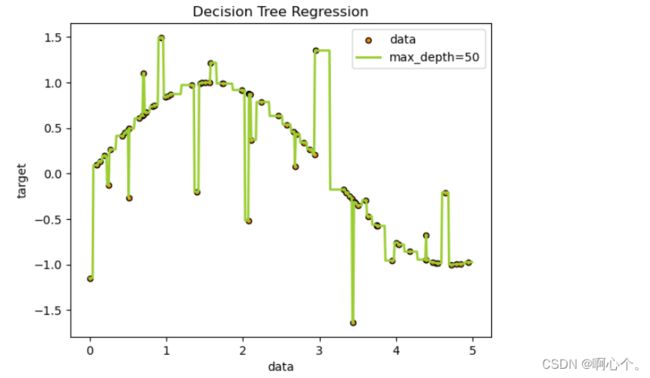
5.2 简单回归树案例：

# Import the necessary modules and libraries
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))

# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=5)
regr_2 = DecisionTreeRegressor(max_depth=50)
regr_1.fit(X, y)
regr_2.fit(X, y)

# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)

# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue", label="max_depth=5", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=50", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()

回归树的最大深度为5：

回归树的最大深度为50：

但是单棵回归树容易陷入过拟合，通常采用集成算法中的提升思想，对回归树进行增强——

• 梯度提升决策树（Gradient Boosting Decision Tree，GBDT）
• XGboost

---

四、回归模型的训练及预测结果

# 引入划分数据集的方式
from sklearn.model_selection import train_test_split
# 引入评价指标
from sklearn.metrics import accuracy_score, recall_score, f1_score

# 引入回归模型
from sklearn.linear_model import LogisticRegression #罗吉斯特回归模型
from sklearn.ensemble import GradientBoostingClassifier #梯度提升回归树

def hr_modeling(features, label):
    # 切分训练集和验证集(测试集)
    f_v = features.values  # 原先的数据是DataFrame,装换为数值，得到特征值
    f_names = features.columns.values  # 得到特征名称
    l_v = label.values
    x_tt, x_validation, y_tt, y_validation = train_test_split(f_v, l_v, test_size=0.2)
    # 将训练集再切分为训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x_tt, y_tt, test_size=0.25)

#将模型的名字和模型函数作为元组添加到列表当中存储；
    models = []
    models.append(("GBDT", GradientBoostingClassifier(max_depth=6, n_estimators=6)))

    models.append(("LogisticRegression",LogisticRegression(C=1000,tol=1e-10,solver='sag',max_iter=10000)))
    # pennalty='l1' or default:'l2'
    # tol 停止运行的阈值计算精度
    # C 正则化因子的比例:越小正则化强度越大
    # solver='sag'随机梯度下降
    # max_iter 最大迭代次数

#循环调用所有模型进行训练、预测
    for clf_name, clf in models:
        clf.fit(x_train, y_train)
        xy_lst = [(x_train, y_train), (x_validation, y_validation), (x_test, y_test)]
        for i in range(len(xy_lst)):
            x_part = xy_lst[i][0]  # 为遍历中的第0部分
            y_part = xy_lst[i][1]  # 为遍历中的第1部分
            y_pred = clf.predict(x_part)
            print(i)  # i是下标，0表示训练集，1表示验证集，2表示测试集
            print(clf_name, "ACC:", accuracy_score(y_part, y_pred))
            print(clf_name, "REC:", recall_score(y_part, y_pred))
            print(clf_name, "F-score:", f1_score(y_part, y_pred))

def regr_test(features, label):
    print("X", features)
    print("Y", label)
    from sklearn.linear_model import LinearRegression, Ridge, Lasso
    regr = LinearRegression()
    # regr=Ridge(alpha=0.8)   #l2正则化
    # regr=Lasso(alpha=0.002)   #l1正则化
    regr.fit(features.values, label.values)
    Y_pred = regr.predict(features.values)
    print("Coef_:", regr.coef_)
    from sklearn.metrics import mean_squared_error
    print("MSE", mean_squared_error(Y_pred, label.values))

def NN(features, label):
    # 切分训练集和验证集(测试集)
    from sklearn.model_selection import train_test_split
    f_v = features.values  # 原先的数据是DataFrame,装换为数值，得到特征值
    f_names = features.columns.values  # 得到特征名称
    l_v = label.values
    x_tt, x_validation, y_tt, y_validation = train_test_split(f_v, l_v, test_size=0.2)
    # 将训练集再切分为训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x_tt, y_tt, test_size=0.25)
    # 引入分类评价指标
    from sklearn.metrics import accuracy_score, recall_score, f1_score
    # 引入回归评价指标
    from sklearn import metrics

    from keras.models import Sequential
    from keras.layers.core import Dense, Activation
    from keras.optimizers import SGD

    mdl = Sequential()
    mdl.add(Dense(50, input_dim=len(f_v[0])))
    mdl.add(Activation("sigmoid"))
    mdl.add(Dense(2))
    mdl.add(Activation("softmax"))
    sgd = SGD(lr=0.01)
    mdl.compile(loss="mse", optimizer="adam")  # "adam" "sgd"
    mdl.fit(x_train, np.array([[0, 1] if i == 1 else [1, 0] for i in y_train]), epochs=500, batch_size=2048)
    xy_lst = [(x_train, y_train), (x_validation, y_validation), (x_test, y_test)]
    for i in range(len(xy_lst)):
        x_part = xy_lst[i][0]  # 为遍历中的第0部分
        y_part = xy_lst[i][1]  # 为遍历中的第1部分
        y_pred = mdl.predict_classes(x_part)
        print(i)  # i是下标，0表示训练集，1表示验证集，2表示测试集
        print("NN", "MSE:", metrics.mean_squared_error(y_part, y_pred))
        print("NN", "RMSE:", metrics.mean_squared_error(y_part, y_pred) ** 0.5)
        print("NN", "MAE:",metrics.mean_absolute_error(y_part, y_pred))
        print("NN", "ACC:", accuracy_score(y_part, y_pred))
        print("NN", "REC:", recall_score(y_part, y_pred))
        print("NN", "F-score:", f1_score(y_part, y_pred))

# 调用所有模型
def main():
    features, label = hr_preprocessing()  # 默认是False,也可以改为True
    regr_test(features[["number_project","average_montly_hours"]],
              features[["last_evaluation"]])
    hr_modeling(features, label)
    NN(features, label)

if __name__ == "__main__":
    main()

线性回归的数据选择：
X        number_project  average_montly_hours
0                 0.0              0.285047
1                 0.6              0.775701
2                 1.0              0.822430
3                 0.6              0.593458
4                 0.0              0.294393
...               ...                   ...
14994             0.0              0.257009
14995             0.0              0.299065
14996             0.0              0.219626
14997             0.8              0.859813
14998             0.0              0.289720

[14999 rows x 2 columns]
Y        last_evaluation
0             0.265625
1             0.781250
2             0.812500
3             0.796875
4             0.250000
...                ...
14994         0.328125
14995         0.187500
14996         0.265625
14997         0.937500
14998         0.250000

[14999 rows x 1 columns]

普通线性回归结果：
回归系数Coef_: [[0.27268022 0.26917309]]
平均绝对误差MSE 0.05953800649100494

岭回归结果：
回归系数Coef_: [[0.27206747 0.26845721]]
平均绝对误差MSE 0.05953807827401485

Lasso回归结果：
回归系数Coef_: [0.25039551 0.24227119]
平均绝对误差MSE 0.0596363767370062

GBDT梯度提升决策树回归算法：
0
GBDT ACC: 0.9805533948216468
GBDT REC: 0.9238770685579196
GBDT F-score: 0.9571393583149646
1
GBDT ACC: 0.979
GBDT REC: 0.9243697478991597
GBDT F-score: 0.9544468546637744
2
GBDT ACC: 0.977
GBDT REC: 0.9150943396226415
GBDT F-score: 0.951646811492642

罗吉斯特回归算法：
0
LogisticRegression ACC: 0.7971996888543171
LogisticRegression REC: 0.37163120567375885
LogisticRegression F-score: 0.462761259935237
1
LogisticRegression ACC: 0.8023333333333333
LogisticRegression REC: 0.3851540616246499
LogisticRegression F-score: 0.48118985126859143
2
LogisticRegression ACC: 0.7783333333333333
LogisticRegression REC: 0.33153638814016173
LogisticRegression F-score: 0.4252376836646499

前馈神经网络训练过程及预测结果

（省略……）

Epoch 498/500
5/5 [==============================] - 0s 399us/step - loss: 0.1220
Epoch 499/500
5/5 [==============================] - 0s 598us/step - loss: 0.1218

Epoch 500/500
5/5 [==============================] - 0s 598us/step - loss: 0.1217

0训练集
NN MSE: 0.13290365596177353
NN RMSE: 0.3645595369233584
NN MAE: 0.13290365596177353
NN ACC: 0.8670963440382264
NN REC: 0.6419354838709678
NN F-score: 0.6996484178804622
1验证集
NN MSE: 0.13833333333333334
NN RMSE: 0.3719318934070233
NN MAE: 0.13833333333333334
NN ACC: 0.8616666666666667
NN REC: 0.6229508196721312
NN F-score: 0.6872645064054257
2测试集
NN MSE: 0.13466666666666666
NN RMSE: 0.3669695718539436
NN MAE: 0.13466666666666666
NN ACC: 0.8653333333333333
NN REC: 0.6263079222720478
NN F-score: 0.6747181964573269