MLE,MAP,贝叶斯理解
概率(probabilty)和统计(statistics)看似两个相近的概念,其实研究的问题刚好相反。
概率研究的问题是已知一个模型和参数预测这个模型产生的结果的特性(例如均值,方差,协方差等等)。
如研究怎么养猪(模型是猪),选好了品种、喂养方式、猪棚的设计等等(选择参数),要知道养出来的猪大概能有多肥,肉质怎么样(预测结果)。
统计研究的问题则相反。统计是有一堆数据,要利用这堆数据去预测模型和参数。仍以猪为例。现在买到了一堆肉,通过观察和判断确定这是猪肉
,这就确定了模型。在实际研究中,也是通过观察数据推测模型是像高斯分布的、指数分布的、拉普拉斯分布的等等,
然后判定这猪的品种、这是圈养猪还是跑山猪还是网易猪等等(推测模型参数)。
总结:概率是已知模型和参数推数据。统计是已知数据推模型和参数。
MLE和MAP都是统计领域的问题,都是用来推测参数的方法。两种不同方法源自贝叶斯思想。
贝叶斯公式就是在描述,你有多大把握能相信一件证据:![]()
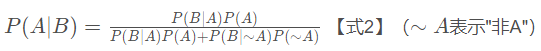 (展开B)
(展开B)
一个本来就难以发生的事情,就算出现某个证据和他强烈相关,也要谨慎。证据很可能来自别的虽然不是很相关,但发生概率较高的事情。
频率学派认为世界是确定的。可直接为事件本身建模,也就是说事件在多次重复实验中趋于一个稳定的值p,那么这个值就是该事件的概率。
同时模型参数是个定值,通过类似解方程组的方式从数据中求得该未知数。使用的参数估计方法-极大似然估计(MLE),
这种方法往往在大数据量的情况下可以很好的还原模型的真实情况。
贝叶斯派认为世界是不确定的,因获取的信息不同而异。假设对世界先有一个预先的估计,然后通过获取的信息来不断调整之前的预估计。
贝叶斯派不试图对事件本身进行建模,而是从旁观者的角度来说。因此对于同一个事件,不同的人掌握的先验不同的话,那么他们所认为的事件状态也会不同。
模型参数源自某种潜在分布,希望从数据中推知该分布。对于数据的观测方式不同或者假设不同,那么推知的该参数也会因此而存在差异。
常用的估计参数的常用方法-最大后验概率估计(MAP),这种方法在先验假设比较靠谱的情况下效果显著,随着数据量的增加,
先验假设对于模型参数的主导作用会逐渐削弱,相反真实的数据样例会大大占据有利地位。
极端情况下,比如把先验假设去掉,或者假设先验满足均匀分布的话,就和极大似然估计就如出一辙了。
经验风险最小化与结构风险最小化是对于损失函数而言的。
经验风险最小化只侧重训练数据集上的损失降到最低;
而结构风险最小化是在经验风险最小化的基础上约束模型的复杂度,使其在训练数据集的损失降到最低的同时,模型不至于过于复杂,
相当于在损失函数上增加了正则项,防止模型出现过拟合状态。这一点也符合奥卡姆剃刀原则:如无必要,勿增实体。
经验风险最小化可以看作是采用了极大似然的参数评估方法,更侧重从数据中学习模型的潜在参数,而且是只看重数据样本本身。
这样在数据样本缺失的情况下,很容易管中窥豹,模型发生过拟合的状态;
结构风险最小化采用了最大后验概率估计的思想来推测模型参数,
不仅仅是依赖数据,还依靠模型参数的先验假设。这样在数据样本不是很充分的情况下,可以通过模型参数的先验假设辅助以数据样本,做到尽可能的还原真实模型分布。
https://blog.csdn.net/u011508640/article/details/72815981
https://blog.csdn.net/zouxy09/article/details/8537620
https://zhuanlan.zhihu.com/p/40024110
