【动手学深度学习PyTorch版】6 权重衰退

上一篇移步【动手学深度学习PyTorch版】5 模型选择 + 过拟合和欠拟合_水w的博客-CSDN博客

目录

一、权重衰退

1.1 权重衰退 weight decay：处理过拟合的最常见方法（L2_penalty）

◼ 权重衰退

◼ 参数更新法则

◼ 权重衰退总结

二、权重衰退代码实现

◼ 使用自定义

◼ 使用框架

---

一、权重衰退

1.1 权重衰退 weight decay：处理过拟合的最常见方法（L2_penalty）

◼ 权重衰退

② 把模型容量控制到比较小，有两种方法，

• 方法一：模型控制的比较小，使得模型中参数比较少。
• 方法二：控制参数选择范围来控制参数容量。

③ 如下图所示，w向量中每一个元素的值都小于θ的根号。

④ 约束就是正则项。每个特征的权重都大会导致模型复杂，从而导致过拟合。控制权重矩阵范数可以使得减少一些特征的权重，甚至使他们权重为0，从而导致模型简单，减轻过拟合。

使用均方范数硬性限制：通常限制参数取值范围来控制模型容量。

1. 一般不限制b，限不限制效果差不多。
2. 小的θ意味着更强的正则项（更强的限制）。

使用均方范数柔性限制：

⑤ λ是一个平滑的，不像以前的硬性限制。

意思就是说，假设我想把模型的复杂度控制的比较低，那么就增加拉姆达，来满足我的需求。

那么，具体是怎么样作用过去的？

⑥ 拉格朗日乘子法原本是用于解决约束条件下的多元函数极值问题。举例，求f(x,y)的最小值，但是有约束C(x,y) = 0。乘子法给的一般思路是，构造一个新的函数g(x,y,λ) = f(x,y) +λC(x,y)，当同时满足g'x = g'y = 0时，函数取到最小值。这结论的几何含义是，当f(x,y)与C(x,y)的等高线相切时，取到最小值。

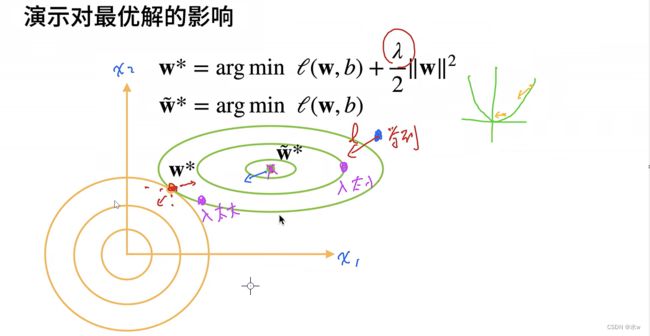
⑦ 具体到机器学习这里，C(x,y) = w^2 -θ。所以黄色圆圈，代表不同θ下的约束条件。θ越小，则最终的parameter离原点越近。

① 绿色的线就是原始损失函数l的等高线，优化原始损失l的最优解(波浪号即最优解)在中心位置。

② 当原始损失加入二分之λ的项后，这个项是一个二次项，假如w就两个值，x1(横轴)、x2(纵轴)，那么在图上这个二次项的损失以原点为中心的等高线为橙色的图所示。所以合并后的损失为绿色的和黄色的线加一起的损失。

③ 当加上损失项后，可以知道原来最优解对应的二次项的损失特别大，因此原来的最优解不是加上二次项后的公式的最优解了。若沿着橙色的方向走，原有l损失值会大一些，但是二次项罚的损失会变小，当拉到平衡点以内时，惩罚项减少的值不足以原有l损失增大的值，这样w * 就是加惩罚项后的最优解。

④ 损失函数加上正则项成为目标函数，目标函数最优解不是损失函数最优解。正则项就是防止达到损失函数最优导致过拟合，把损失函数最优点往外拉一拉。鼓励权重分散，将所有额特征运用起来，而不是依赖其中的少数特征，并且权重分散的话它的内积就小一些。

⑤ l2正则项会对大数值的权值进行惩罚。

◼ 参数更新法则

当前的权重会变小 —— 衰退 decay。 

◼ 权重衰退总结

我们在真正的优化时，通过一个拉姆达来控制模型的强度，每次对权重做了一次放小，就等价于是说权重的衰退过程。

二、权重衰退代码实现

◼ 使用自定义

权重衰退是最广泛使用的正则化的技术之一。

首先，导入包，像以前一样生成一些人工数据集：

其中，噪音是均值为0，方差为0.01的正态分布。

当数据集越小，模型越复杂的时候，越容易发生过拟合。所以我们的训练样本n_train选择了一个很小的20，num_inputs为特征维度为200。这样很容易发生过拟合。

训练时，训练稍微长一些，因为训练数据集（20）比较小，所以设置迭代100次。

训练过程：

1. 初始化模型种类、参数、损失、epoch、超参数
2. epoch循环
   1. batch_size为单位的循环
      1. 损失计算
      2. 损失反向传播
         优化器优化
         优化器梯度清零

损失函数中添加正则项即可。（添加 罚）

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5 # 数据越简单，模型越复杂，越容易过拟合。num_inputs为特征维度
true_w, true_b = torch.ones((num_inputs,1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train) # 生成人工数据集
train_iter = d2l.load_array(train_data, batch_size)     # 读取
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

# 初始化模型参数w和b
def init_params():
    w = torch.normal(0,1,size=(num_inputs,1),requires_grad=True)     # w是200x1的向量，需要梯度
    b = torch.zeros(1,requires_grad=True)     # b为全0的一个标量
    return [w,b]


# 核心：定义L2范数惩罚
def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2


# 定义训练函数，输入参数lambd
def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss   # 线性回归，使用平方损失函数
    num_epochs, lr = 100, 0.003   # 选择训练稍微长一些，因为训练数据集（20）比较小，所以迭代100次
    # 动画效果
    animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['train','test'])   

    for epoch in range(num_epochs):    # 每一次数据迭代  
        for X, y in train_iter:        #  每一次从迭代器里拿出x和y
            #with torch.enable_grad():
            l = loss(net(X),y) + lambd * l2_penalty(w) # 计算损失时，原始损失函数加上lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w,b],lr,batch_size)
        if(epoch+1) % 5 == 0:
            if(epoch+1) % 5 ==0:
                animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net,test_iter,loss)))
    print('w的L2范数是',torch.norm(w).item()) 

help(d2l.synthetic_data) # 查看函数用法

# 忽略正则化直接训练
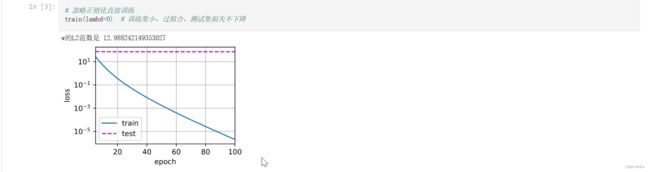
train(lambd=0)  # 训练集小，过拟合，测试集损失不下降

从动画效果中可以看出，如果没有lambd的话，没有规约，就是完全没有L2范数。训练数据集小，可以看到训练数据集的loss一直在往下降，但是测试集损失不下降。测试集损失和训练集损失的中间有一个特别特别大的差值gap，那么这就是一个明显的过拟合。

也就是说，模型一直去拟合训练函数，去拟合噪音， 但是在新的数据集上，在我的测试数据集上，其实看不到有任何的进展。这是非常严重的过拟合。

那么，如果lambd=3的话，可以看到有一定的效果，

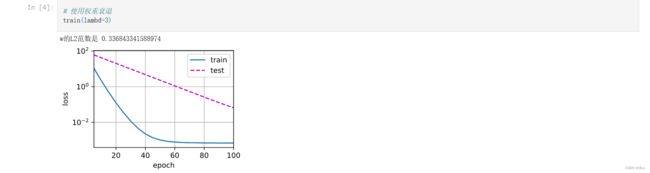
# 使用权重衰退
train(lambd=3)

从动画效果中可以看出，训练数据集的loss一直在往下降的时候，测试集损失也是在往下降，虽然之间还是有一定的过拟合，但是可以看到有一定的效果。L2范数使得测试集损失和训练集损失的中间不会有一个特别特别大的差值gap。

如果再多迭代迭代，测试集损失还是有可能会赶上训练集损失一点的。

因为我们本身的这个训练数据集小，所以过拟合情况是无法避免的。

后续的话，我们还可以继续尝试两种方法：

• 调大lambd，看看效果；
• 调大迭代次数，测试集损失还是很有可能会赶上训练集损失一点的；

◼ 使用框架

惩罚项既可以写在目标函数里面，也可以写在训练算法里面，每一次在更新之前把当前的w乘以衰退因子weight_decay 。

# 简洁实现
def train_concise(wd):
    net = nn.Sequential(nn.Linear(num_inputs,1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss()
    num_epochs, lr = 100, 0.003
    trainer = torch.optim.SGD([{"params":net[0].weight,"weight_decay":wd},{"params":net[0].bias}],lr=lr) 
# 惩罚项既可以写在目标函数里面，也可以写在训练算法里面，每一次在更新之前把当前的w乘以衰退因子weight_decay                     
    animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['train','test'])                   
    for epoch in range(num_epochs):
        for X, y in train_iter:
            with torch.enable_grad():
                trainer.zero_grad()
                l = loss(net(X),y)
            l.backward()
            trainer.step()
            if(epoch + 1) % 5 == 0:
                animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net,test_iter,loss)))
    print('w的L2范数是',net[0].weight.norm().item()) 

# 这些图看起来和我们从零开始实现权重衰减时的图相同
train_concise(0)

train_concise(3)

这些图看起来和我们上文实现的权重衰减时的图相同。