06-梯度下降优化(Lasso/Ridge/ElasticNet)

1、归一化 (Normalization)

由于不同方向的陡峭度是不一样的，即不同维度的数值大小是不同。也就是说梯度下降的快慢是不同的,归一化的一个目的是，使得梯度下降在不同维度 $\theta$ 参数（不同数量级）上，可以步调一致协同的进行梯度下降。归一化的本质就要把各个特征维度 $x_1、x_2、\dots \dots 、x_n$ 的数量级统一，来做到无量纲化。

1.1、最大值最小值归一化

也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0 - 1]之间。转换函数如下：
.
$X=\frac{X-X\_min}{X\_max-X\_min}$

通过公式可以发现,该方式受离群值的影响比较大.
使用scikit-learn函数演示：

import numpy as np
from sklearn.preprocessing import MinMaxScaler
x_1 = np.random.randint(1,10,size = 10)
x_2 = np.random.randint(100,300,size = 10)
x = np.c_[x_1,x_2]    # 将数组放到一起
print('归一化之前的数据：')
min_max_scaler = MinMaxScaler()
x_ = min_max_scaler.fit_transform(x)
print('归一化之后的数据：')
display(x_)

1.2、0-均值标准化

这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化，也叫做Z-score标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：
.
$X^{\ast }=\frac{X-\mu }{\sigma }$
其中μ为所有样本数据的均值，σ为所有样本数据的标准差。
相对于最大值最小值归一化来说，因为标准归一化除以了标准差，而标准差的计算会考虑到所有样本数据，所以受到离群值的影响会小一些，这就是除以方差的好处！但是，0-均值标准化不一定会把数据缩放到 0 ~ 1 之间了。既然是0均值，也就意味着，有正有负！
使用scikit-learn函数：

import numpy as np
from sklearn.preprocessing import StandardScaler
x_1 = np.random.randint(1,10,size = 10)
x_2 = np.random.randint(100,300,size = 10)
x = np.c_[x_1,x_2]
print('归一化之前的数据：')
standard_scaler = StandardScaler()
x_ = standard_scaler.fit_transform(x)
print('归一化之后的数据：')
display(x_)

注意：
我们在做特征工程的时候，很多时候如果对训练集的数据进行了预处理，比如这里讲的归一化，那么未来对测试集的时候，和模型上线来新的数据的时候，都要进行相同的数据预处理流程，而且所使用的均值和方差是来自当时训练集的均值和方差!
通过把 scaler 对象持久化， 回头模型上线的时候再加载进来去对新来的数据进行处理。

import joblib
joblib.dump(standard_scaler,'scale') # 持久化
standard_scaler = joblib.load('scale') # 加载
standard_scaler.transform(x) # 使用

2、正则化 Regularization

2.1、过拟合欠拟合

1. 欠拟合（under fit）：还没有拟合到位，训练集和测试集的准确率都还没有到达最高，学的还不到位。
2. 过拟合（over fit）：拟合过度，训练集的准确率升高的同时，测试集的准确率反而降低。学的过度了（走火入魔），做过的卷子都能再次答对（死记硬背），考试碰到新的没见过的题就考不好（不会举一反三）。
3. 恰到好处（just right）：过拟合前，训练集和测试集准确率都达到巅峰。好比，学习并不需要花费很多时间，理解的很好，考试的时候可以很好的把知识举一反三。
   正则化就是防止过拟合，增加模型的鲁棒性，鲁棒是 Robust 的音译，也就是强壮的意思。正则化(鲁棒性调优)的本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力， W 在数值上越小越好，这样能抵抗数值的扰动。同时为了保证模型的正确率 W 又不能极小。

• 常用的惩罚项有L1 正则项或者 L2 正则项,分别对应曼哈顿距离(x+y),和欧式距离(平方再开方).
• 当我们把多元线性回归损失函数加上 L2 正则的时候，就诞生了 Ridge 岭回归。当我们把多元线性回归损失函数加上 L1 正则的时候，就孕育出来了 Lasso 回归。

2.2、套索回归（Lasso）

先从线性回归开始，其损失函数如下：

$J(\theta )=\frac{1}{2}\sum _{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
L1正则化的损失函数，令$J_0=J(\theta )$：

$J=J_0+\alpha \ast \sum _{i=1}^n|w_i|$
令 $L_1=\alpha \ast \sum _{i=1}^n|w_i|$ ：

$J=J_0+L_1$
其中 $J_0$ 是原始的损失函数，加号后面的一项是L1正则化项， $\alpha$ 是正则化系数。注意到 L1正则化是权值的绝对值之和。$J$ 是带有绝对值符号的函数，因此 $J$ 是不完全可微的。机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。当我们在原始损失函数 $J_0$ 后面添加L1正则项时，相当于对 $J_0$ 做了一个约束。令$L_1=\alpha \ast \sum _{i=1}^n|w_i|$ ，则 $J=J_0+L_1$ ，此时我们的任务变成在 $L_1$ 约束下求出 $J_0$ 取最小值的解。考虑二维的情况，即只有两个权值 $w_1、w_2$ ，此时 $L_1=|w_1|+|w_2|$。
用 $\lambda$ 表示L1正则化系数：

${\theta }_j^{n+1}={\theta }_j^n-\eta \sum _{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}-\eta \ast \lambda \ast sgn(w_i)$

L1正则化和普通线性回归系数对比：

• 和没有正则项约束线性回归对比，可知L1正则化，将方程系数进行了缩减，部分系数为0，产生稀疏模型
• $\alpha$ 越大，模型稀疏性越强，越多的参数为0
• Lasso回归源码解析：
  • alpha：正则项系数
  • fit_intercept：是否计算 $w_0$ 截距项
  • normalize：是否做归一化
  • precompute：bool 类型，默认值为False，决定是否提前计算Gram矩阵来加速计算
  • max_iter：最大迭代次数
  • tol：结果的精确度
  • warm_start：bool类型，默认值为False。如果为True，那么使⽤用前⼀次训练结果继续训练。否则从头开始训练

import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor

# 1、创建数据集X，y
X = 2*np.random.rand(100, 20)
w = np.random.randn(20,1)
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)

print('原始方程的斜率：',w.ravel())
print('原始方程的截距：',b)

lasso = Lasso(alpha= 0.5)
lasso.fit(X, y)
print('套索回归求解的斜率：',lasso.coef_)
print('套索回归求解的截距：',lasso.intercept_)

# 线性回归梯度下降方法
sgd = SGDRegressor(penalty='l2',alpha=0, l1_ratio=0)
sgd.fit(X, y.reshape(-1,))
print('随机梯度下降求解的斜率是：',sgd.coef_)
print('随机梯度下降求解的截距是：',sgd.intercept_)

2.3、岭回归（Ridge）

也是先从线性回归开始，其损失函数如下：

$J(\theta )=\frac{1}{2}\sum _{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
L2正则化的损失函数（对L2范数，进行了平方运算），令$J_0=J(\theta )$：

$J=J_0+\alpha \ast \sum _{i=1}^n(w_i{)}^2$
令 $L_2=\alpha \ast \sum _{i=1}^n(w_i{)}^2$ ：

$J=J_0+L_2$
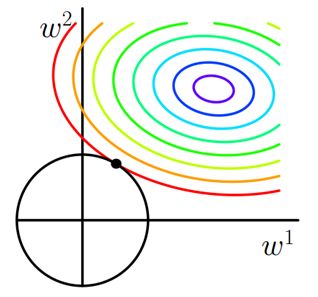
二维平面下 L2 正则化的函数图形是个圆（绝对值的平方和，是个圆），与方形相比，被磨去了棱角。因此 $J_0$ 与 $L_2$ 相交时使得 $w_1、w_2$ 等于零的机率小了许多（这个也是一个很直观的想象），这就是为什么L2正则化不具有稀疏性的原因，因为不太可能出现多数 w 都为0的情况（这种情况就叫稀疏性）！

用 $\lambda$ 表示L2正则化系数：
${\theta }_j^{n+1}={\theta }_j^n(1-\eta \ast \lambda )-\eta \ast \sum _{i=1}^n(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$

L2正则化和普通线性回归系数对比：

• 和没有正则项约束线性回归对比，可知L2正则化，将方程系数进行了缩小
• $\alpha$ 增大求解出来的方程斜率变小
• Ridge回归源码解析：
  • alpha：正则项系数
  • fit_intercept：是否计算 $w_0$ 截距项
  • normalize：是否做归一化
  • max_iter：最大迭代次数
  • tol：结果的精确度
  • solver：优化算法的选择

import numpy as np
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor

# 1、创建数据集X，y
X = 2*np.random.rand(100, 5)
w = np.random.randint(1,10,size = (5,1))
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)

print('原始方程的斜率：',w.ravel())
print('原始方程的截距：',b)

ridge = Ridge(alpha= 1, solver='sag')
ridge.fit(X, y)
print('岭回归求解的斜率：',ridge.coef_)
print('岭回归求解的截距：',ridge.intercept_)

# 线性回归梯度下降方法
sgd = SGDRegressor(penalty='l2',alpha=0,l1_ratio=0)
sgd.fit(X, y.reshape(-1,))
print('随机梯度下降求解的斜率是：',sgd.coef_)
print('随机梯度下降求解的截距是：',sgd.intercept_)

2.4、Elastic-Net算法使用

  Elastic-Net 回归，即岭回归和Lasso技术的混合。弹性网络是一种使用 L1， L2 范数作为先验正则项训练的线性回归模型。 这种组合允许学习到一个只有少量参数是非零稀疏的模型，就像 Lasso 一样，但是它仍然保持一些像 Ridge 的正则性质。我们可利用 l1_ratio 参数控制 L1 和 L2 的凸组合。
  弹性网络在很多特征互相联系（相关性，比如身高和体重就很有关系）的情况下是非常有用的。Lasso 很可能只随机考虑这些特征中的一个，而弹性网络更倾向于选择两个。
  在实践中，Lasso 和 Ridge 之间权衡的一个优势是它允许在迭代过程中继承 Ridge 的稳定性。

弹性网络回归和普通线性回归系数对比：

import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor

# 1、创建数据集X，y
X = 2*np.random.rand(100, 20)
w = np.random.randn(20,1)
b = np.random.randint(1,10,size = 1)
y = X.dot(w) + b + np.random.randn(100, 1)

print('原始方程的斜率：',w.ravel())
print('原始方程的截距：',b)

model = ElasticNet(alpha= 1, l1_ratio = 0.7)
model.fit(X, y)
print('弹性网络回归求解的斜率：',model.coef_)
print('弹性网络回归求解的截距：',model.intercept_)

# 线性回归梯度下降方法
sgd = SGDRegressor(penalty='l2',alpha=0, l1_ratio=0)
sgd.fit(X, y.reshape(-1,))
print('随机梯度下降求解的斜率是：',sgd.coef_)
print('随机梯度下降求解的截距是：',sgd.intercept_)

3、多项式回归

3.1、多项式回归基本概念

 升维的目的是为了去解决欠拟合的问题的，也就是为了提高模型的准确率为目的的，因为当维度不够时，说白了就是对于预测结果考虑的因素少的话，肯定不能准确的计算出模型。
 在做升维的时候，最常见的手段就是将已知维度进行相乘（或者自乘）来构建新的维度，如下图所示。普通线性方程，无法拟合规律，必须是多项式，才可以完美拟合曲线规律，图中是二次多项式。
 对于多项式回归来说主要是为了扩展线性回归算法来适应更广泛的数据集，比如我们数据集有两个维度 $x_1、x_2$，那么用多元线性回归公式就是：$\hat{y}=w_0+w_1{x}_1+w_2{x}_2$，当我们使用二阶多项式升维的时候，数据集就从原来的 $x_1、x_2$扩展成了$x_1、x_2、x_1^2、x_2^2、x_1{x}_2$ 。因此多元线性回归就得去多计算三个维度所对应的w值：$\hat{y}=w_0+w_1{x}_1+w_2{x}_2+w_3{x}_1^2+w_4{x}_2^2+w_5{x}_1{x}_2$ 。
  此时拟合出来的方程就是曲线，可以解决一些线性回归的欠拟合问题！

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 1、创建数据，并进行可视化
X = np.linspace(-1,11,num = 100)
y = (X - 5)**2 + 3*X -12 + np.random.randn(100)
X = X.reshape(-1,1)
plt.scatter(X,y)

# 2、创建预测数据
X_test = np.linspace(-2,12,num = 200).reshape(-1,1)

# 3、不进行升维 + 普通线性回归
model_1 = LinearRegression()
model_1.fit(X,y)
y_test_1 = model_1.predict(X_test)
plt.plot(X_test,y_test,color = 'red')

# 4、多项式升维 + 普通线性回归
X = np.concatenate([X,X**2],axis = 1)
model_2 = LinearRegression()
model_2.fit(X,y)
# 5、测试数据处理，并预测
X_test = np.concatenate([X_test,X_test**2],axis = 1)
y_test_2 = model_2.predict(X_test)

# 6、数据可视化，切片操作
plt.plot(X_test[:,0],y_test_2,color = 'green')