最优化--梯度下降法(python)
目录
-
- 一.基础
- 二.一元函数求解
-
- (1)代码
- (2)结果
- (3)分析
- 三.二元函数求解
-
- (1)代码
- (2)结果
一.基础
梯度下降法是一个一阶最优化算法,它需要用到函数的一阶导数/偏导。
如果要找到一个函数的局部极小值,我们必须向函数当前点对应梯度(导数/偏导)的反方向进行规定步长的点迭代搜索。比如 f’(x)>0 ,那么当前就处于递增区间,要向x减小的方向搜索。
如果要找到一个函数的局部极大值,我们必须向函数当前点对应梯度(导数/偏导)的正方向进行规定步长的点迭代搜索。
基本式子:
x n + 1 = x n − α f ′ ( x n ) x_{n+1}=x_{n}-αf^{'}(x_{n}) xn+1=xn−αf′(xn)
∙ \bullet ∙ 形象的说就是沿着梯度一直下降,当变化量处于精度范围内或迭代次数达到指定次数后停止迭代,找到最终结果值!
∙ \bullet ∙ 其中α为学习率,我们可以指定它的大小,它越大迭代次数越少。
二.一元函数求解
我们求解 f(x) = 0.25*(x-0.5)2 + 1 的局部极小值
(1)代码
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"] = ["SimHei"] #解决中文乱码问题
plt.rcParams["axes.unicode_minus"] = False #使负号正常显示
#函数关系式
def f1(x):
return 0.25 * (x-0.5) ** 2 + 1
#一阶导关系式
def h1(x):
return 0.25 * 2 * (x-0.5)
#存放迭代过程中变化的点的坐标,最后作图
GD_X = []
GD_Y = []
#x初始值
x=4
#存放y的变化量
y_change = f1(x)
#存放当前y的值
y_current = f1(x)
#记录迭代次数
item_num=0
#学习率alpha
alpha=0.5
GD_X.append(x)
GD_Y.append(y_current)
#迭代过程
while y_change>1e-10 and item_num<100:
item_num += 1;
x = x-alpha*h1(x)
#当前f1(x)
temp = f1(x)
y_change = np.abs(y_current-temp)
y_current = temp
GD_X.append(x)
GD_Y.append(y_current)
print("最终解:(%.5f,%.5f)"%(x,y_current))
print("迭代次数:",item_num)
print(GD_X)
print(GD_Y)
#进行作图
X = np.arange(-4,4.5,0.05)
Y = np.array(list(map(lambda t:f1(t),X)))
plt.figure(facecolor='w')
plt.plot(X,Y,'r-',linewidth=2)
plt.plot(GD_X,GD_Y,'bo--',linewidth=2)
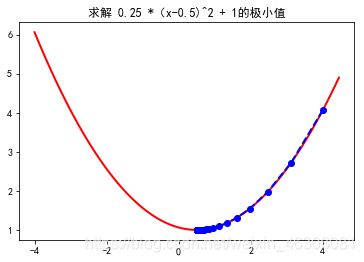
plt.title('求解 0.25 *(x-0.5)^2 + 1的极小值')
plt.show()
(2)结果
最终解:(0.50002,1.00000)
迭代次数: 42
[4, 3.125, 2.46875, 1.9765625, 1.607421875, 1.33056640625, 1.1229248046875, 0.967193603515625, 0.8503952026367188, 0.7627964019775391, 0.6970973014831543, 0.6478229761123657, 0.6108672320842743, 0.5831504240632057, 0.5623628180474043, 0.5467721135355532, 0.5350790851516649, 0.5263093138637487, 0.5197319853978115, 0.5147989890483586, 0.511099241786269, 0.5083244313397017, 0.5062433235047763, 0.5046824926285822, 0.5035118694714367, 0.5026339021035775, 0.5019754265776831, 0.5014815699332623, 0.5011111774499467, 0.5008333830874601, 0.500625037315595, 0.5004687779866963, 0.5003515834900223, 0.5002636876175167, 0.5001977657131376, 0.5001483242848532, 0.5001112432136399, 0.5000834324102299, 0.5000625743076724, 0.5000469307307543, 0.5000351980480657, 0.5000263985360494, 0.500019798902037]
[4.0625, 2.72265625, 1.968994140625, 1.5450592041015625, 1.306595802307129, 1.17246013879776, 1.09700882807374, 1.0545674657914788, 1.0306941995077068, 1.017265487223085, 1.0097118365629854, 1.0054629080666793, 1.003072885787507, 1.0017284982554728, 1.0009722802687033, 1.0005469076511457, 1.0003076355537694, 1.0001730449989954, 1.0000973378119349, 1.0000547525192134, 1.0000307982920575, 1.0000173240392825, 1.0000097447720964, 1.0000054814343042, 1.000003083306796, 1.000001734360073, 1.000000975577541, 1.0000005487623669, 1.0000003086788314, 1.0000001736318427, 1.0000000976679115, 1.0000000549382002, 1.0000000309027377, 1.0000000173827899, 1.0000000097778192, 1.0000000055000233, 1.0000000030937632, 1.0000000017402417, 1.000000000978886, 1.0000000005506233, 1.0000000003097256, 1.0000000001742206, 1.0000000000979992]
(3)分析
我们可以看到当α=0.5时,经过42次迭代后所得结果基本上为精确解。
我们试着改变α的值查看结果
alpha = 3.2
最终解:(0.49999,1.00000)
迭代次数: 25
[4, -1.6000000000000005, 1.7600000000000007, -0.25600000000000067, 0.9536000000000004, 0.2278399999999997, 0.6632960000000002, 0.40202239999999984, 0.5587865600000002, 0.4647280639999999, 0.5211631616000001, 0.48730210303999993, 0.507618738176, 0.4954287570944, 0.50274274574336, 0.498354352553984, 0.5009873884676096, 0.4994075669194342, 0.5003554598483395, 0.4997867240909963, 0.5001279655454023, 0.49992322067275863, 0.5000460675963448, 0.4999723594421931, 0.5000165843346841, 0.49999004939918956]
[4.0625, 2.1025000000000005, 1.3969000000000005, 1.1428840000000002, 1.0514382400000002, 1.0185177664, 1.006666395904, 1.00239990252544, 1.0008639649091584, 1.000311027367297, 1.000111969852227, 1.0000403091468018, 1.0000145112928487, 1.0000052240654256, 1.000001880663553, 1.0000006770388792, 1.0000002437339965, 1.0000000877442388, 1.000000031587926, 1.0000000113716534, 1.0000000040937953, 1.0000000014737662, 1.0000000005305558, 1.000000000191, 1.00000000006876, 1.0000000000247535]
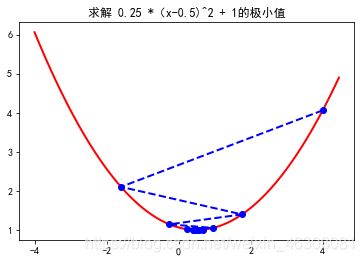
当α相对而言变大时,搜索点的位置会左右来回横跳直到找到结果!
三.二元函数求解
我们求解 f(x,y) = 0.6*(x+y)2 -x*y+ 1 的局部极小值
(1)代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#二元函数表达式
def f1(x,y):
return 0.6 * (x + y) ** 2 - x * y + 1
#对x求偏导
def hx1(x,y):
return 0.6 * 2 * (x + y) - y
#对y求偏导
def hy1(x,y):
return 0.6 * 2 * (x + y) - x
#初始值
x=4
y=4
#存放迭代的点坐标及对应函数值列表
GD_X=[]
GD_Y=[]
GD_Z=[]
#对应函数值的变化量及真实值
z_change=f1(x,y)
z_current=f1(x,y)
#学习率
alpha=1.2
#迭代次数
item_num=0
GD_X.append(x)
GD_Y.append(y)
GD_Z.append(z_current)
#迭代过程
while z_change>1e-10 and item_num<100:
item_num+=1
#改变x和y的值
x1=x
y1=y
x=x-alpha*hx1(x1,y1)
y=y-alpha*hy1(x1,y1)
#存储当前情况下对应函数值
temp=f1(x,y)
z_change = np.abs(z_current-temp)
z_current=temp
GD_X.append(x)
GD_Y.append(y)
GD_Z.append(z_current)
print(u'最终结果:(%.5f,%.5f,%.5f)'%(x,y,z_current))
print("迭代次数:",item_num)
print(GD_X)
print(GD_Y)
print(GD_Z)
#作图
X=np.arange(-4,4,0.05)
Y=np.arange(-4,4,0.05)
X,Y=np.meshgrid(X,Y)
Z=np.array(list(map(lambda t:f1(t[0],t[1]),zip(X.flatten(),Y.flatten()))))
Z.shape=X.shape
fig = plt.figure(facecolor='w')
ax=Axes3D(fig)
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X,GD_Y,GD_Z,'ro--')
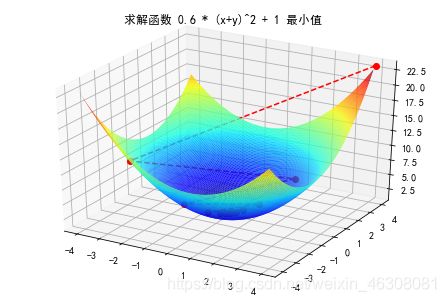
ax.set_title('求解函数 0.6 * (x+y)^2 + 1 最小值')
plt.show()
(2)结果
最终结果:(-0.00001,-0.00001,1.00000)
迭代次数: 35
[4, -2.7199999999999998, 1.8495999999999997, -1.2577279999999997, 0.8552550399999994, -0.5815734271999995, 0.39546993049599966, -0.26891955273727974, 0.18286529586135025, -0.12434840118571816, 0.0845569128062883, -0.057498700708276035, 0.03909911648162771, -0.026587399207506843, 0.018079431461104654, -0.012294013393551163, 0.008359929107614787, -0.005684751793178053, 0.003865631219361074, -0.00262862922916553, 0.0017874678758325593, -0.0012154781555661397, 0.0008265251457849746, -0.0005620370991337826, 0.00038218522741097205, -0.00025988595463946097, 0.00017672244915483342, -0.0001201712654252867, 8.171646048919494e-05, -5.556719313265255e-05, 3.778569133020373e-05, -2.5694270104538523e-05, 1.7472103671086186e-05, -1.1881030496338599e-05, 8.079100737510244e-06, -5.493788501506965e-06]
[4, -2.7199999999999998, 1.8495999999999997, -1.2577279999999997, 0.8552550399999994, -0.5815734271999995, 0.39546993049599966, -0.26891955273727974, 0.18286529586135025, -0.12434840118571816, 0.0845569128062883, -0.057498700708276035, 0.03909911648162771, -0.026587399207506843, 0.018079431461104654, -0.012294013393551163, 0.008359929107614787, -0.005684751793178053, 0.003865631219361074, -0.00262862922916553, 0.0017874678758325593, -0.0012154781555661397, 0.0008265251457849746, -0.0005620370991337826, 0.00038218522741097205, -0.00025988595463946097, 0.00017672244915483342, -0.0001201712654252867, 8.171646048919494e-05, -5.556719313265255e-05, 3.778569133020373e-05, -2.5694270104538523e-05, 1.7472103671086186e-05, -1.1881030496338599e-05, 8.079100737510244e-06, -5.493788501506965e-06]
[23.4, 11.357759999999999, 5.789428223999998, 3.214631610777599, 2.024045656823561, 1.4735187117152144, 1.218955052297115, 1.101244816182186, 1.0468156030026428, 1.021647534828422, 1.0100098201046623, 1.004628540816396, 1.0021402372735015, 1.0009896457152672, 1.0004576121787394, 1.0002115998714491, 1.000097843780558, 1.00004524296413, 1.0000209203466137, 1.0000096735682742, 1.00000447305797, 1.0000020683420052, 1.0000009564013432, 1.000000442239981, 1.0000002044917673, 1.0000000945569931, 1.0000000437231535, 1.0000000202175863, 1.0000000093486119, 1.0000000043227981, 1.000000001998862, 1.0000000009242738, 1.0000000004273841, 1.0000000001976224, 1.0000000000913807, 1.0000000000422544]