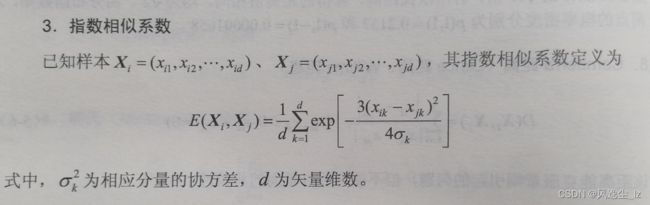聚类分析详细解读python
文章目录
- 相似性测度
-
- 1.距离测度
-
-
- 1.1 欧式距离
- 1.2 街坊距离(Manhattan距离)
- 1.3切式(Chebyshev)距离
- 1.4明氏(Minkowski)距离
- 1.5 马氏(Mahalanobis)距离
- 1.6 Camberra距离
-
- 2.相似测度
-
-
- 2.1角度相似系数(夹角余弦)
- 2.2指数相似系数
-
- 3.类间距离测度方法
-
-
- 3.1最短距离法
- 3.2 最长距离法
- 3.3 中间距离法
- 3.4 重心法
- 3.5平均距离法
-
- 聚类准则函数
-
- 1.误差平方和准则
- 2.加权平均平方距离准则
- 3.类间距离和准则
- 4.离散度矩阵
- 聚类算法总结:
-
- 1.基于阈值的聚类算法
-
-
- 1.1最近邻规则的聚类算法
- 1.2最大最小距离聚类算法
-
- 2.动态聚类算法
-
-
- 2.1C均值聚类算法
- 2.2 ISODATA聚类算法
-
- 3.基于密度的聚类算法
-
-
- 3.1 DBSCAN聚类算法
-
- 4.层次聚类
- 部分参考文献:
相似性测度
样本相似性度量是聚类分析的基础,针对具体问题,选择适当的相似性度量是保证聚类效果的基础。
1.距离测度
1.1 欧式距离
对于样本X1和样本X2,我们假设他们是具有二维特征的样本比如说有两个人,我们只看他们的两个特征,身高(X11和X11)和体重(X12,X22),我们将他们在特征空间中进行表示,如下图:
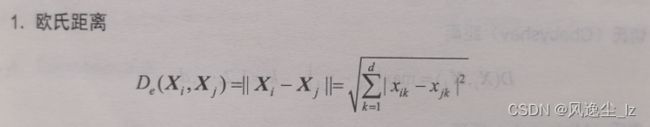
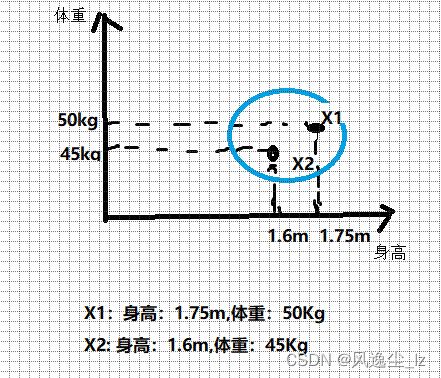
求欧式距离意味着,我们要求两个样本之间对应特征之间的差的的平方和,最后开根号。
代码实现:
def European(x1,x2):
result=0
for i in range(len(x1)):
result+=pow((x1[i]-x2[i]),2)
return math.sqrt(result)
量纲对聚类结果具有很大的影响,也就是说横轴的和纵轴的单位不同,但是用欧氏距离作为样本之间的距离,进行聚类的时候,我们因为量纲的不同产生了不同的结果。
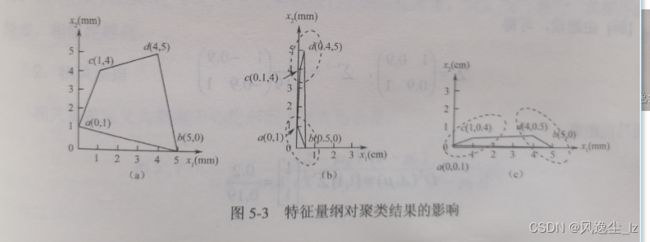
1.2 街坊距离(Manhattan距离)

图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
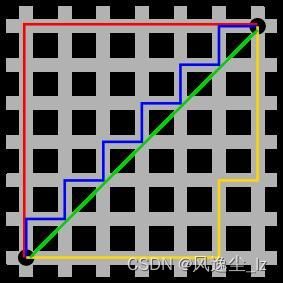
代码实现:
def Manhattan(x1,x2):
result=0
for i in range(len(x1)):
result+=abs(x1[i]-x2[i])
return result
1.3切式(Chebyshev)距离
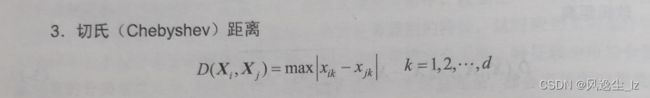
也就是说,每两个样本他们所对应的特征之间的距离最大的作为切比雪夫距离,例如,前面所说的身高和体重,X1和X2的身高特征进行相减求绝对值,体重同样处理,比较哪个更大,那么这个更大的值就作为他们切式距离。
代码实现:
def Chebyshev(x1,x2): #传入两个样本
result=[]
for i in range(len(x1)):
result.append(abs(x1[i]-x2[i]))
result=max(result)
return result
1.4明氏(Minkowski)距离
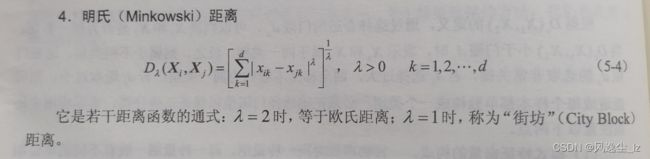
闵可夫斯基距离(Minkowski Distance)不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
def Minkowski(x1,x2,p):
result=0
for i in range(len(x1)):
result+=pow(abs(x1[i]-x2[i]),p)
return pow(result,1/p)
1.5 马氏(Mahalanobis)距离
在介绍马氏距离之前,我们先来看如下几个概念:
方差: 方差是标准差的平方,而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。
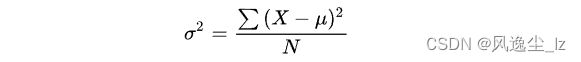
协方差: 标准差与方差是描述一维数据的,当存在多维数据时,我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中,变量之间相关性的统计量。比如说,一个人的身高与他的体重的关系,这就需要用协方差来衡量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。

协方差矩阵: 当变量多了,超过两个变量了。那么,就用协方差矩阵来衡量这么多变量之间的相关性。假设 X 是以 n 个随机变数(其中的每个随机变数是也是一个向量,当然是一个行向量)组成的列向量:

例子:
如果我们以厘米为单位来测量人的身高,以克(g)为单位测量人的体重。每个人被表示为一个两维向量,如一个人身高173cm,体重50000g,表示为(173,50000),根据身高体重的信息来判断体型的相似程度。
我们已知小明(160,60000);小王(160,59000);小李(170,60000)。根据常识可以知道小明和小王体型相似。但是如果根据欧几里得距离来判断,小明和小王的距离要远远大于小明和小李之间的距离,即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。
以克(g)为单位测量人的体重,数据分布比较分散,即方差大,而以厘米为单位来测量人的身高,数据分布就相对集中,方差小。马氏距离的目的就是把方差归一化,使得特征之间的关系更加符合实际情况。
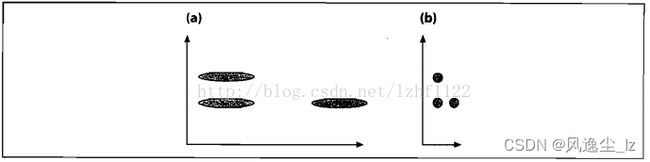
图(a)展示了三个数据集的初始分布,看起来竖直方向上的那两个集合比较接近。在我们根据数据的协方差归一化空间之后,如图(b),实际上水平方向上的两个集合比较接近。

from numpy import *
import numpy
def get_mahalanobis(x, i, j):
xT = x.T # 求转置
D = numpy.cov(xT) # 求协方差矩阵
invD = numpy.linalg.inv(D) # 协方差逆矩阵
assert 0 <= i < x.shape[0], "点 1 索引超出样本范围。"
assert -1 <= j < x.shape[0], "点 2 索引超出样本范围。"
x_A = x[i]
x_B = x.mean(axis=0) if j == -1 else x[j]
tp = x_A - x_B
return numpy.sqrt(dot(dot(tp, invD), tp.T))
if __name__ == '__main__':
# 初始化数据点集,或者从其它地方加载
x = numpy.array([[3, 4], [5, 6], [2, 2], [8, 4]])
# 求第0个点到均值之间的马氏距离(j为-1时代表均值)
print(get_mahalanobis(x, 0, -1))
# 求第0个点到第1个点之间的马氏距离
print(get_mahalanobis(x, 0, 1))
# 求第2个点到第3个点之间的马氏距离(索引从0开始算起)
print(get_mahalanobis(x, 2, 3))
1.6 Camberra距离
def Canberra(x1,x2):
result=0
for i in range(len(x1)):
result+=abs(x1[i]-x2[i])/abs(x1[i]+x2[i])
return result
2.相似测度
2.1角度相似系数(夹角余弦)
2.2指数相似系数
3.类间距离测度方法
在聚类算法中我们要得到两个类之间的距离是多少,需要有一个衡量,是在两个类中找两个最近的样本了作为两个类之间的距离了?还是以最远的两个样本作为类间距离,下面正是探讨这些情况。
3.1最短距离法
用最短距离作为两个类之间的距离,也就是说计算两个类中,每个样本两两之间的距离,选取最小的那个距离作为两个类的距离。
3.2 最长距离法
3.3 中间距离法
3.4 重心法
3.5平均距离法
聚类准则函数
距离准则函数不仅会影响聚类的质量,而且还可以评价一种聚类结果的质量。

1.误差平方和准则
2.加权平均平方距离准则
3.类间距离和准则
4.离散度矩阵
聚类算法总结:
1.基于阈值的聚类算法
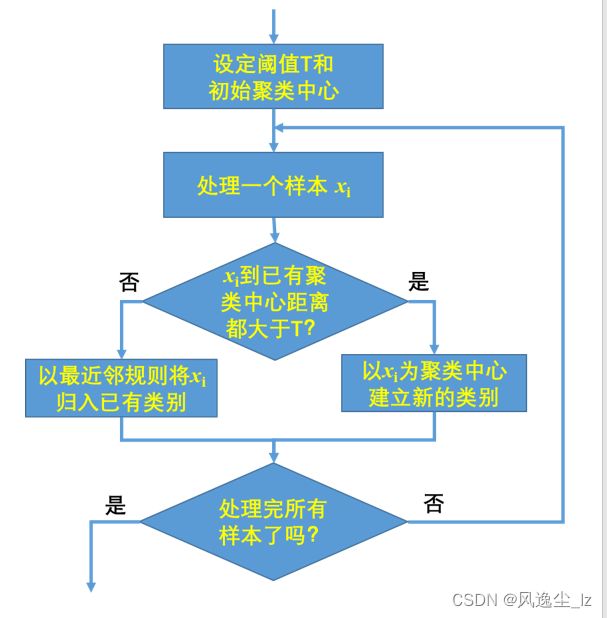
1.1最近邻规则的聚类算法
代码实现:
#202001170218 罗同学 智能2班
import math
def knn_cluster(data,t):
#任意选取一个聚类中心
z=[data[0]]
#计算聚类中心
get_cluster_z(data,z,t)
#进行归类
result=classify(data,z,t)
return result
def get_cluster_z(data,z,t):
#遍历所有的样本
for adata in data:
min_distance=get_distance(adata,z[0])
#遍历聚类中心,找出这个样本距离所有聚类中心的最小距离
for i in range(len(z)):
distance=get_distance(adata,z[i])
if distance<min_distance:
min_distance=distance
#如果这个距离所有聚类中心的最小距离满足>阈值
if min_distance>t:
z.append(adata) #将该样本加入聚类中心列表
def classify(data,z,t):
result=[[] for i in range(len(z))]
#遍历所有样本
for adata in data:
min_distance = t
index=0
#遍历所有聚类中心,得到当前样本和其他聚类中心的距离
for i in range(len(z)):
tem_distance=get_distance(adata,z[i])
if min_distance>tem_distance:
min_distance=tem_distance
index=i
result[index].append(adata)
return result
def get_distance(x,y):
result=0
for i in range(len(x)):
result=pow((x[i]-y[i]),2)
return math.sqrt(result)
data = [[0, 0],[3, 8],[1, 1],[2, 2],[5, 3],[4, 8],[6, 3],[5, 4],[6, 4],[7, 5]]
t = 0.5
result =knn_cluster(data, t)
for i in range(len(result)):
print("----------第"+ str(i+1)+"个聚类----------")
print(result[i])
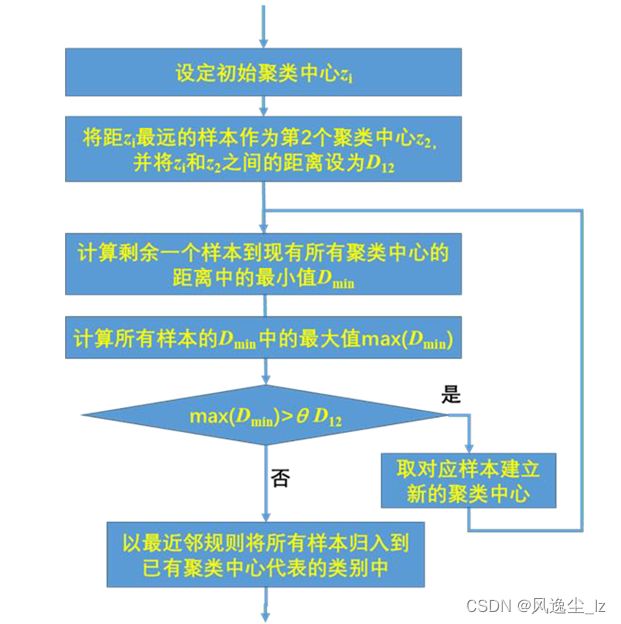
1.2最大最小距离聚类算法
代码实现:
#202001170218 罗璋 智能2班
import math
def max_min_cluster(data,t):
#选取第一个样本作为第一个聚类中心
z=[data[0]]
#求第二个聚类中心,并且求阈值
T=get_threshold_z2(data,z,t)
#求所有的聚类中心
get_all_z(data,z,T)
#进行聚类
result=classify(data,z,T)
return result
def classify(data,z,T):
#建立一个列表,进行存储各个类别
result=[[] for i in range(len(z))]
#遍历整个样本集
for adata in data:
min_distance=T #满足条件的基本要求
index=0
#遍历所有的聚类中心点,求该样本点离哪一个比较近
for i in range(len(z)):
tem_distance=get_distance(adata,z[i])
if tem_distance<min_distance:
min_distance=tem_distance
#最终找到的那个最近的聚类中心点,要记录它的位置,以便加入该类
index=i
#遍历完所有的聚类中心之后我们得出该样本属于哪一类
result[index].append(adata)
return result
def get_all_z(data,z,T):
max_min_distance=0
index=0
#遍历所有的点,求其到各个聚类中心点的距离,求出最大最小距离
for i in range(len(data)):
tem_distance=[]
#求该样本点到所有聚类中心的距离,存储到列表中
for j in range(len(z)):
tem_distance.append(get_distance(data[i],z[j]))
#找出最小的距离
min_distance=min(tem_distance)
#求出最大最小距离
if min_distance>max_min_distance:
max_min_distance=min_distance
index=i #记录所有最小距离中的最大的那个的索引,便于后续进行,判断
#遍历完所有的点,我们判断最大最小距离的这个样本是否满足聚类中心点
if max_min_distance>T:
z.append(data[index])
#继续进行迭代求其他的聚类中心
get_all_z(data,z,T)
def get_threshold_z2(data,z,t):
max_distance=0
index=0
for i in range(len(data)):
distance=get_distance(data[i],z[0])
#求出离第一个聚类中心的最大距离的那个样本作为第二个聚类中心
if distance>max_distance:
max_distance=distance
index=i
z.append(data[index])
T=max_distance*t
return T
def get_distance(x,y):
distance=0
for i in range(len(x)):
distance+=pow((x[i]-y[i]),2)
return math.sqrt(distance)
data = [[0, 0],[3, 8],[1, 1],[2, 2],[5, 3],[4, 8],[6, 3],[5, 4],[6, 4],[7, 5]]
t = 0.5
result = max_min_cluster(data, t)
for i in range(len(result)):
print("----------第"+ str(i+1)+"个聚类----------")
print(result[i])
2.动态聚类算法
2.1C均值聚类算法
2.2 ISODATA聚类算法
3.基于密度的聚类算法
3.1 DBSCAN聚类算法
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
from sklearn import metrics
UNCLASSIFIED = 0
NOISE = -1
# 计算数据点两两之间的距离
def getDistanceMatrix(datas):
N,D = np.shape(datas)
dists = np.zeros([N,N])
for i in range(N):
for j in range(N):
vi = datas[i,:]
vj = datas[j,:]
dists[i,j]= np.sqrt(np.dot((vi-vj),(vi-vj)))
return dists
# 寻找以点cluster_id 为中心,eps 为半径的圆内的所有点的id
def find_points_in_eps(point_id,eps,dists):
index = (dists[point_id]<=eps)
return np.where(index==True)[0].tolist()
def expand_cluster(dists, labs, cluster_id, seeds, eps, min_points):
i = 0
while i< len(seeds):
# 获取一个临近点
Pn = seeds[i]
# 如果该点被标记为NOISE 则重新标记
if labs[Pn] == NOISE:
labs[Pn] = cluster_id
# 如果该点没有被标记过
elif labs[Pn] == UNCLASSIFIED:
# 进行标记,并计算它的临近点 new_seeds
labs[Pn] = cluster_id
new_seeds = find_points_in_eps(Pn,eps,dists)
# 如果 new_seeds 足够长则把它加入到seed 队列中
if len(new_seeds) >=min_points:
seeds = seeds + new_seeds
i = i+1
def dbscan(datas, eps, min_points):
# 计算 所有点之间的距离
dists = getDistanceMatrix(datas)
# 将所有点的标签初始化为UNCLASSIFIED
n_points = datas.shape[0]
labs = [UNCLASSIFIED]*n_points
cluster_id = 0
# 遍历所有点
for point_id in range(0, n_points):
# 如果当前点已经处理过了
if not(labs[point_id] == UNCLASSIFIED):
continue
# 没有处理过则计算临近点
seeds = find_points_in_eps(point_id,eps,dists)
# 如果临近点数量过少则标记为 NOISE
if len(seeds)<min_points:
labs[point_id] = NOISE
else:
# 否则就开启一轮簇的扩张
cluster_id = cluster_id+1
# 标记当前点
labs[point_id] = cluster_id
expand_cluster(dists, labs, cluster_id, seeds,eps, min_points)
return labs, cluster_id
# 绘图
def draw_cluster(datas,labs, n_cluster):
plt.cla()
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1,n_cluster)]
for i,lab in enumerate(labs):
if lab ==NOISE:
plt.scatter(datas[i,0],datas[i,1],s=16.,color=(0,0,0))
else:
plt.scatter(datas[i,0],datas[i,1],s=16.,color=colors[lab-1])
plt.show()
if __name__== "__main__":
# 数据1
centers = [[1, 1], [-1, -1], [1, -1]]
datas, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
random_state=0)
## 数据2
# file_name = "spiral"
# with open(file_name+".txt","r",encoding="utf-8") as f:
# lines = f.read().splitlines()
# print("lines:\n",lines)
# lines = [line.split("\t")[:-1] for line in lines]
# print("lines:\n",lines)
# datas = np.array(lines).astype(np.float32)
# print("datas",datas[:5])
# 数据正则化
datas = StandardScaler().fit_transform(datas)
print("数据正则化后",datas[:5])
eps = 0.3 #半径
min_points = 10 #阈值
labs, cluster_id = dbscan(datas, eps=eps, min_points=min_points)
print("labs of my dbscan")
print(labs)
db = DBSCAN(eps=eps, min_samples=min_points).fit(datas)
skl_labels = db.labels_
print("labs of sk-DBSCAN")
print(skl_labels)
draw_cluster(datas,labs, cluster_id)
4.层次聚类
代码实现:
import math
#求两者的欧式距离
def get_distance(data1,data2):
distance=0
for i in range(len(data1)):
distance+=pow(data1[i]-data2[i],2)
return math.sqrt(distance)
#两个类求他们之间的最小距离
def get_min_distance(list1,list2):
#先将两个类中每个类的第一个样本之间的欧式距离作为两个类之间的最小距离
min_distance=get_distance(list1[0],list2[0])
#分别计算两个类中两两之间的距离,求出最小距离
for i in range(len(list1)):
for j in range(len(list2)):
tem_distance=get_distance(list1[i],list2[j])
if tem_distance<min_distance:
min_distance=tem_distance
return min_distance
def hierarchical_cluster(data,t):
#将每个样本都作为一个单独的类
res=[[aData] for aData in data]
#计算所有类中最近的两个类之间的距离,并依次进行聚类
step2(res,t)
return res
def step2(res,t):
#先假设1类和2类之间的距离为最小距离
min_distance=get_min_distance(res[0],res[1])
#记录聚类的两个类的下标
index1=0
index2=1
#计算所有类中两两之间的距离,得到最小的两个类之间的距离,并记录下标
for i in range(len(res)):
for j in range(i+1,len(res)):
tem_distance=get_min_distance(res[i],res[j])
if tem_distance<min_distance:
min_distance=tem_distance
index1=i
index2=j
#先进行阈值判断,对找出的最小距离的两个类进行聚类,在原类存放列表中删除index2位置的类,再进行递归处理
if min_distance<=t:
res[index1].extend(res[index2])
res.pop(index2)
step2(res,t)
data=[[0,3,1,2,0],[1,3,0,1,0],[3,3,0,0,1],[1,1,0,2,0],[3,2,1,2,1],[4,1,1,1,0]]
t=math.sqrt(5)
result=hierarchical_cluster(data,t)
for i in range(len(result)):
print("------第"+str(i+1)+"个聚类---------")
print(result[i])
部分参考文献:
马氏距离