机器学习 jupyter Python无监督学习 聚类 k-meas算法
1.有监督学习与无监督学习
1.1 有监督学习
又称监督学习,就是人们常说的分类,通过已有的训练样本(即已知数据以及其对应的输出)去训练得到一个最优模型,再利用这个模型将所有的输入映射为相应的输出。
1.2 无监督学习
无监督学习(也有人叫非监督学习,反正都差不多)则是另一种研究的比较多的学习方法,它与监督学习的不同之处,在于我们事先没有任何训练样本(训练集),而需要直接对数据进行建模。
2.聚类
2.1 聚类和分类的区别
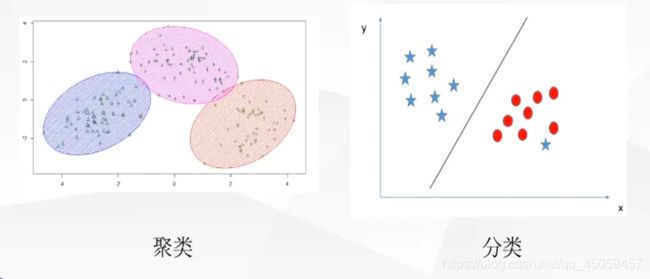
聚类和分类的区别:聚类是无监督学习任务,不知道真实的样本标记,只把相似度高的样本聚合在一起;分类是监督学习任务,利用已知的样本标记训练学习器预测未知样本的类别。
2.2 聚类的作用
2.2.1 寻找优质用户
2.2.2 社区发现
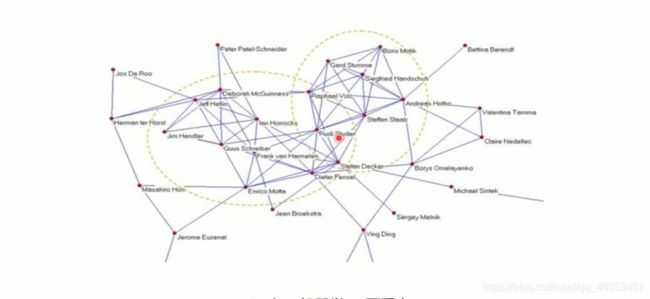
比如将每一个看作一个人,这些人之间存在这联系,我们把联系比较多的聚成一个类别,认为是同一个社群
2.2.3 异常点监控
将银行后台数据归类为两个类别,比如正常一个类别,不正常一个类别。大多数情况下,数据都会归为正常类别的那一个类,但是出现异常点的时候,就会归为另一个类别,所以这个点可能是信用卡诈骗或者是黑客攻击。
例如将后台数据分成一个个特征,根据这些特征做聚类。然后发现异常点。
3.常见的聚类算法(k-means算法)
3.1 算法核心
算法接受参数K;然后将事先输入的n个数据对象划分成k个聚类。使得所获得聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较低。(物以类聚)
3.2 算法思想
以空间中k个样本点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐步更新各聚类中心的值,直至找得到最好的聚类结果。
3.3 算法步骤
3.3.1 先从没有标签的元素集合A中随机选K个元素,作为k个子集(簇)各自的重心。注:所有样本点的初识簇可以为0
3.3.2 分别计算所有的样本点到k个子集重心的距离(这里的距离可以是欧式距离),根据距离将样本划分到距离最近的子集。(注:求样本点到所有质心的距离)
3.3.3根据聚类的结果,重新计算重心(重心的计算方法是计算各子集中所有样本各个维度的算数平均值)
(4)重复第2步,即将集合A中的所有元素按照新的质心重新聚类。
(5)重复第4步,直至聚类结果不再发生变化。(就是所有的样本点所属的簇不再发生变化)
4.深入理解k-means算法
4.1 取4个点(1,1),(2,1),(4,3),(5,4)
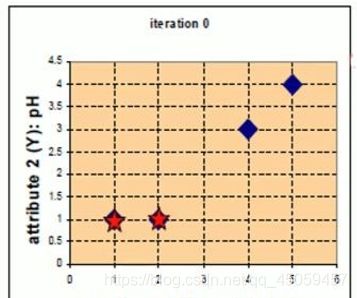
假设取(1,1),(2,1)为两个分类中心点
4.2 计算各个点到质心的距离,并把他们分簇

0是点(1,1)到分类中心点(1,1)的距离,
1是点(2,1)到分类中心点(1,1)的距离,
3.61是点(4,3)到分类中心点(1,1)的距离,
5是点(5,4)到分类中心点(1,1)的距离;
1是点(1,1)到分类中心点(2,1)的距离,
0是点(2,1)到分类中心点(2,1)的距离,
2.83是点(4,3)到分类中心点(2,1)的距离
4.24是点(5,4)到分类中心点(2,1)的距离。
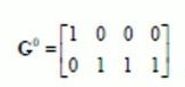
0<1,说明(1,1)距离分类中心点(1,1)近,所以将(1,1)分为第一簇,
1>0,说明(2,1)距离分类中心点(2,1)近,所以将(2,1)分为第二簇,
3.61>2.83,说明(4,3)距离分类中心点(2,1)近,所以将(4,3)分为第二簇,
5>4.24,说明(5,4)距离分类中心点(2,1)近,所以将(5,4)分为第二簇。
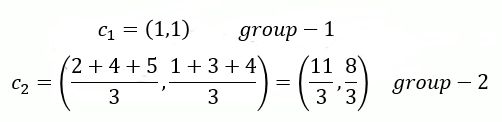
最后,更换分类中心点,分类中心点变为(1,1),(11/3,8/3)。
问题1:为什么不停止计算呢?
答:算法终止的判定条件:样本所属的簇不再发生变化,算法终止。
4.3 第二次计算各个点到质心的距离,并把他们分簇


0是点(1,1)到分类中心点(1,1)的距离,
1是点(2,1)到分类中心点(1,1)的距离,
3.61是点(4,3)到分类中心点(1,1)的距离,
5是点(5,4)到分类中心点(1,1)的距离;
3.14是点(1,1)到分类中心点(11/3,8/3)的距离,
2.36是点(2,1)到分类中心点(11/3,8/3)的距离,
0.47是点(4,3)到分类中心点(11/3,8/3)的距离,
1.89是点(5,4)到分类中心点(11/3,8/3)的距离。

0<3.14,说明(1,1)距离分类中心点(1,1)近,所以将(1,1)分为第一簇,
1<2.36,说明(2,1)距离分类中心点(1,1)近,所以将(2,1)分为第一簇,
3.61>0.47,说明(4,3)距离分类中心点(11/3,8/3近,所以将(4,3)分为第二簇,
1<2.36,说明(5,4)距离分类中心点(11/3,8/3近,所以将(5,4)分为第二簇。
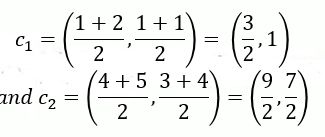
最后,更换分类中心点,分类中心点变为(3/2,1),(9/2,7/2)。
4.4 第三次计算各个点到质心的距离,并把他们分簇

![]()
0.5是点(1,1)到分类中心点(3/2,1)的距离,
1是点(2,1)到分类中心点(3/2,1)的距离,
3.61是点(4,3)到分类中心点(3/2,1)的距离,
5是点(5,4)到分类中心点(3/2,1)的距离;
4.30是点(1,1)到分类中心点(9/2,7/2)的距离,
3.54是点(2,1)到分类中心点(9/2,7/2)的距离,
0.71是点(4,3)到分类中心点(9/2,7/2)的距离,
0.71是点(5,4)到分类中心点(9/2,7/2)的距离。

0.5<4.30,说明(1,1)距离分类中心点(1,1)近,所以将(1,1)分为第一簇,
0.5<3.54,说明(2,1)距离分类中心点(1,1)近,所以将(2,1)分为第一簇,
3.20>0.7,说明(4,3)距离分类中心点(11/3,8/3近,所以将(4,3)分为第二簇,
4.61<0.71,说明(5,4)距离分类中心点(11/3,8/3近,所以将(5,4)分为第二簇。
聚类不发生变化,算法迭代停止
5.具体案列
5.1 问题
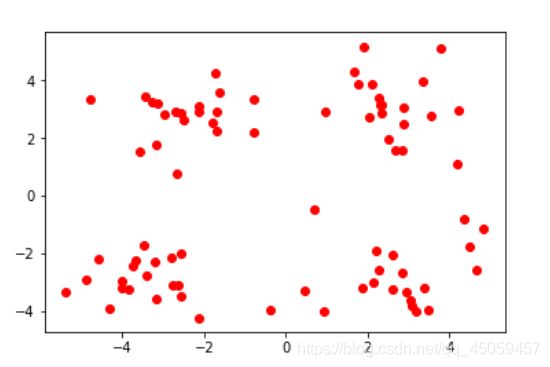
根据数据集testSet2.txt,利用sklearn里的Kmeans算法完成聚类分类,并画出图形。
testSet2.txt部分展示:

5.2 思路
5.2.1导入相关包
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
5.2.2 画出散点图,并建立模型和训练模型,计算分类中心点和分簇结果
dataSet=np.genfromtxt('testSet2.txt')#读取文件
plt.scatter(dataSet[:,0],dataSet[:,1],c='r')#画出散点图
KM=KMeans(n_clusters=4)#根据散点图大致确定为4簇,n_clusters簇数
KM.fit(dataSet)#训练数据
centers=KM.cluster_centers_#这里是最终的聚类分类点的分类中心点
print(centers)
result=KM.predict(dataSet)#预测结果
print('分簇的结果',result)
# print(KM.labels_)
5.2.3 画图。分类之后的图和分类中心点
#画图
#画样本点
#属于第一簇的样本点用红色三角表示。。。。。。。
mark=['^r','sb','*g','oy']
for i,d in enumerate(dataSet):
#enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
#d[0],d[1]是样本点的横纵坐标,分簇的结果为0,1,2,3,所以可以和mark对应上
plt.plot(d[0],d[1],mark[result[i]])
#画出分类中心点
markcentor=['+r','+b','+g','+y']
for i,centor in enumerate(centers):
#centor[0],centor[1]是一个质心的横纵坐标。
plt.plot(centor[0],centor[1],markcentor[i],markersize=30)