基于Frenet坐标系的无人车轨迹规划详解与实现
目的
本文详细讲解Frenet坐标系中的无人车轨迹规划方法,并探讨在ROS下的代码实现,先看下仿真的效果。
1 简介
Frenet坐标系中的无人车轨迹规划方法(简称Frenet方法)是 Moritz Werling 在2010年的论文《Optimal Trajectory Generation for Dynamic Street Scenarios in a Frene´t Frame》里首次提出的。其思想被广泛采用,甚至Matlab官方都加入了相应的函数:trajectoryOptimalFrenet,效果如下面左侧的动画。此外,一些开源的无人驾驶项目也借鉴了其核心思想,例如百度的Apollo无人驾驶项目就使用了Frenet坐标系。因为很出名,所以网上已经有很多基于Frenet方法的规划模块开源代码,我们后面的实现也基于一个公开的开源项目:SDC_ND_T3P1_Path_Planning。
2 Frenet方法讲解
2.1 规划的目标
如果问:无人车规划轨迹的宗旨是什么?笔者认为有两个:安全和舒适。安全肯定是首要的,如果规划出来的轨迹导致撞车显然是任何人都无法接收的。至于舒适,则主要面向有人乘坐的无人车,如果无人车动不动就加速或者急刹车你坐在上面肯定会抱怨,当然对于拉货的车辆也不是说可以任意加减速,这对车辆的执行器件也是伤害。因此这两个指标是一般的规划方法都要考虑的。Frenet方法设计的出发点也考虑了这两个方面。
2.2 Frenet坐标系
Frenet坐标系是这个方法最大的特点。既然我们选择了Frenet方法,那么原因是什么?它的特点又是什么?
笔者认为Frenet方法的一个优点是思想简单,容易理解,而且性能不错。当然Frenet方法也有很多缺点,例如依赖参考线、坐标系的变换比较麻烦等等,这些我们后面再说。网上可以搜到很多作者对这种方法的介绍(例如AdamShan),但是他们描述的都很粗糙而且不够形象,很多细节没有提,导致读者不能快速而深刻地领会这个方法,后果就是不能自己实现,接下来笔者仔细介绍下Frenet方法。
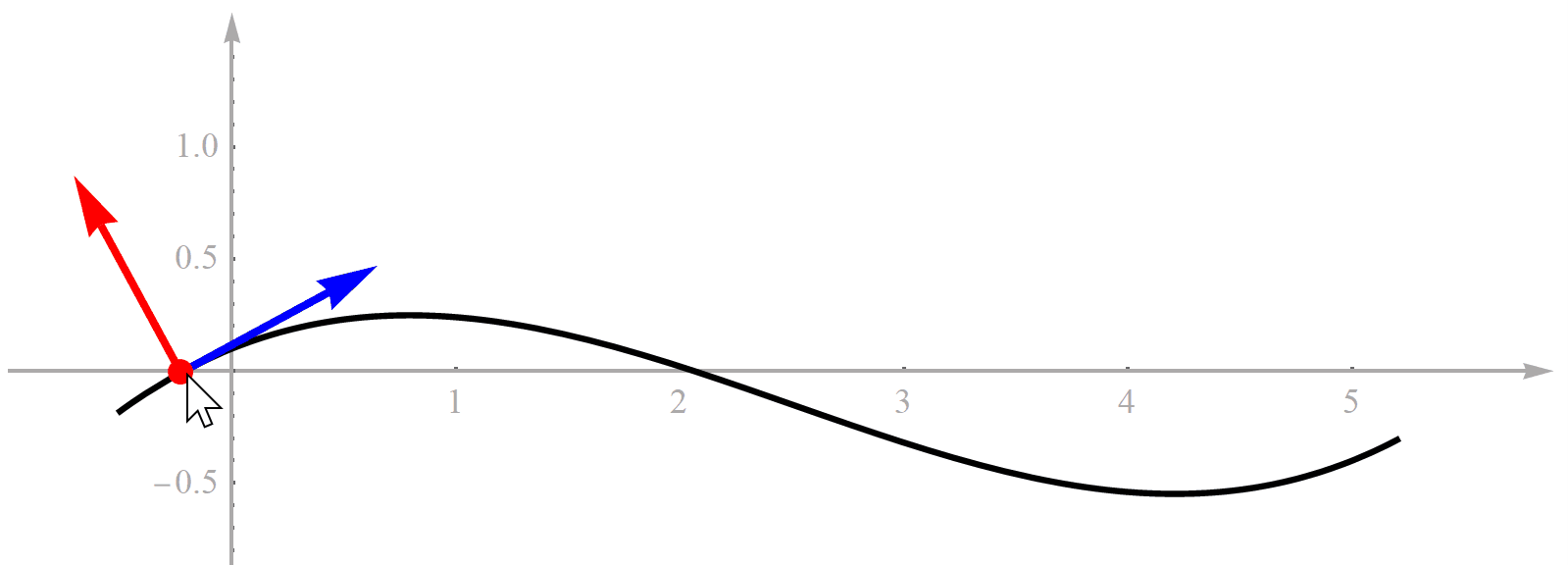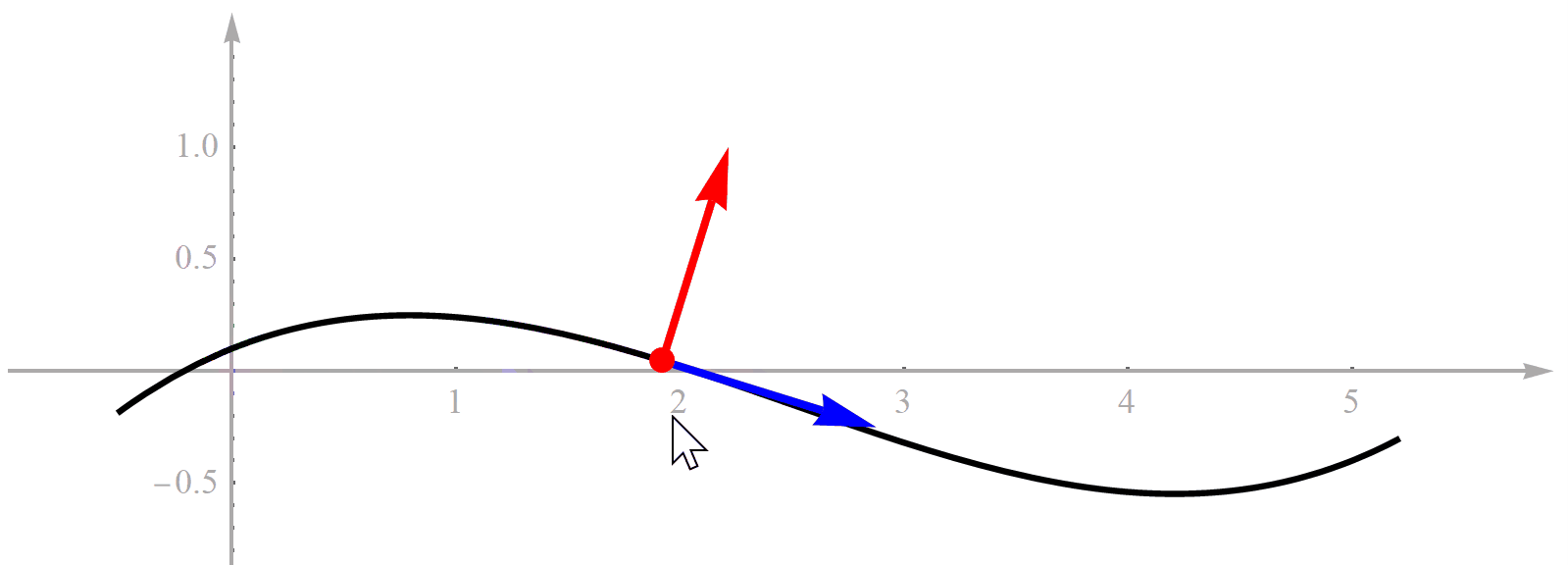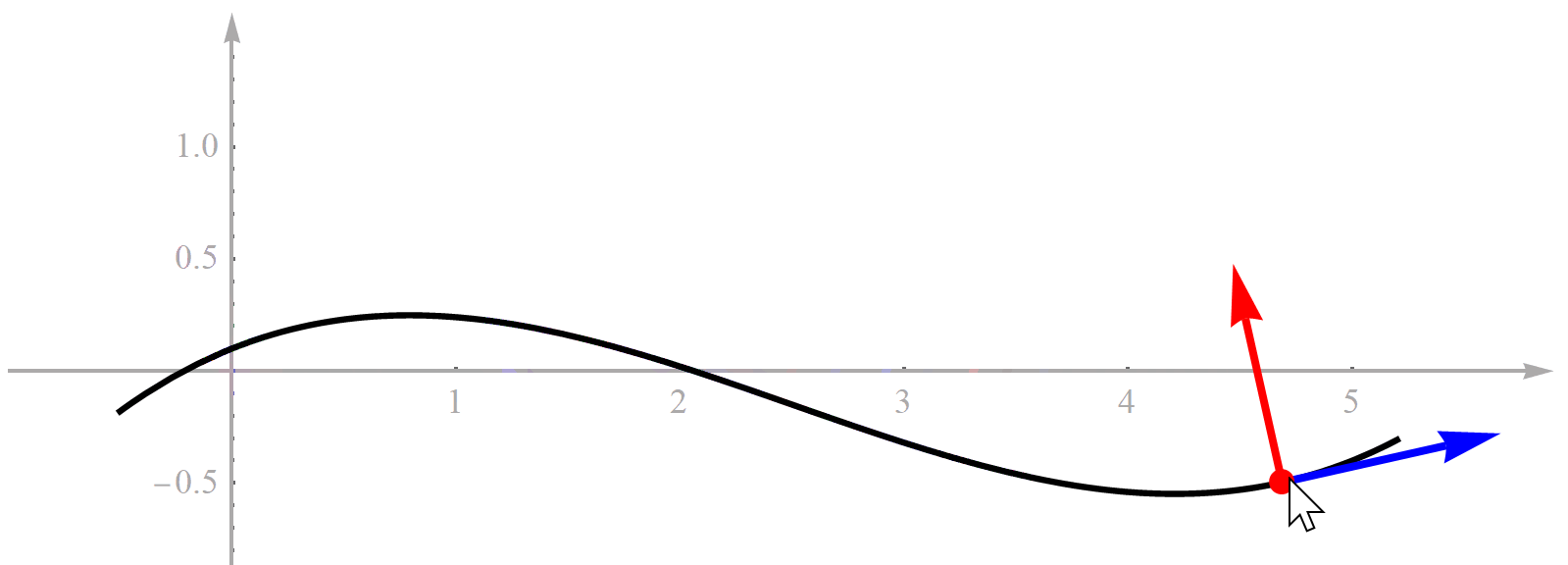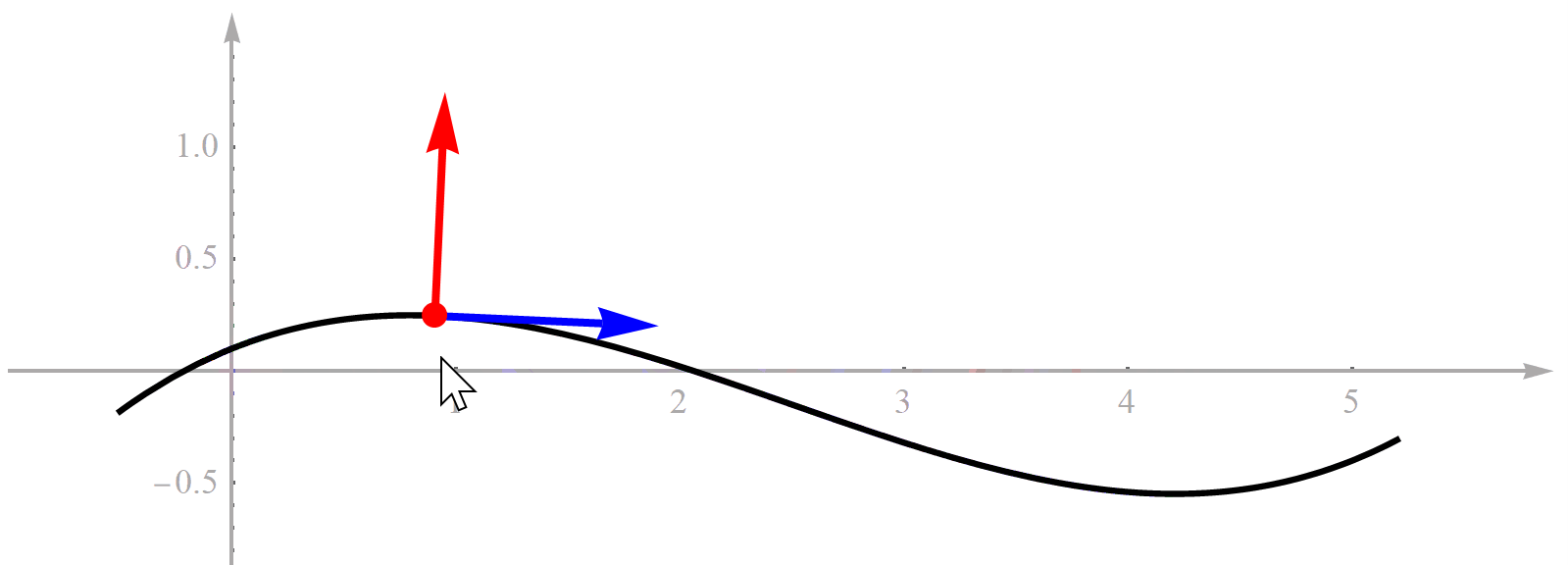
既然方法的名字叫“基于Frenet坐标系的轨迹规划”,那首先必须理解什么是“Frenet坐标系”。我们想象一下自己开车时,最简单省劲的策略就是沿着道路上的导引线开。这也是车道线存在的意义。我们把车道线想象成一条连续的曲线。对于一条曲线,如果它是光滑可微的,那么曲线上的每一点处都可以求切线。求切线的目的是它定义了一个方向向量。切线有了,再逆时针旋转90°就能得到一条法线,如下图所示。很显然,切线和法线还有它们的交点就构成了一个直角坐标系,这个坐标系就是传说中的Frenet坐标系。所以Frenet坐标系也是一个直角坐标系,没什么神秘的,大家不用害怕。为了便于理解,我特意用Mathematica做了一个演示动画。黑色曲线代表道路参考线,用鼠标能选择曲线上不同的点,随着鼠标移动道路上的点也在不断变化,对应的Frenet坐标系就跟着变化,很形象了吧。
2.3 Frenet坐标系中的规划
现在你知道了什么是Frenet坐标系?那么“在Frenet坐标系下进行轨迹规划”又是什么意思呢?这其实就是说我们计算的轨迹是相对于Frenet坐标系表示的。用文字描述这个过程实在是不够直观,所以笔者又制作了一个动画,见下图。笔者用一个最简单的例子,就是一次多项式来展示。下面的左图是一次多项式的图像,当然了一次多项式就是一个直线。注意,这是在一个直角坐标系中画出来的,如果我们把这个坐标系的横轴当成曲线的弧长,纵轴当成到曲线的距离,那么在一个参考曲线中画出来又是什么样的呢,就是下图右侧的图展示的。这跟Frenet坐标系有什么关系呢?如果把这个直线离散成一些点,那把每个点的横坐标看成弧长 s s s,根据弧长能找到曲线上一个唯一的点,这个点决定一个唯一的Frenet坐标系。我们再利用这个点的纵坐标 d d d,在这个曲线上的点的基础上沿着Frenet坐标系的法向量移动长度 d d d就得到一个新的点,这个新的点就是Frenet坐标系中的点。所以,我们在规划时依然是在直角坐标系中的进行的,规划出来曲线后再离散,然后转换到Frenet坐标系中就行了。这里不太好理解的一点就是,左图的坐标系到底是什么。想象一下,如果你把右图中的黑色参考曲线拉直了,拉成一条直线,那两边的图像就变成完全一样的了。所以,左图其实是相对于参考曲线的变化,而右图是相对变化叠加到(一个固定的)参考曲线上得到的曲线,这么说应该容易理解了。
现在我们理解“在Frenet坐标系下进行轨迹规划”的含义了,说白了就是两条曲线的叠加。虽说原理清楚了,但是笔者还要交代几句要注意的细节。上面提到的弧长 s s s指的是道路参考线(center line)上的动点与道路参考线的起点之间曲线的长度(也就是上面右图中的红色曲线,可能看不太清),而不是你规划的轨迹(蓝色曲线)的长度。这个初学者很容易傻傻分不清楚,因为笔者一开始也搞混了,导致看后面的推导公式总是理解不了。
所以,Frenet坐标系仅仅是一种描述方式,地位和全局直角坐标系一样。规划使用的曲线表达式与坐标系和参考曲线也没关系,例如你可以在Frenet坐标系下使用任何一种曲线表达方式,例如B样条、贝塞尔曲线、Cycloid都可以,不必像原始论文一样局限于单段多次多项式。举个例子,华为的专利中就采用了分段样条曲线的表达方式,如下图。

2.4 参考线
Frenet坐标系是依附于参考线的,因此参考线在整个规划过程中是必不可少的。在百度Apollo自动驾驶项目中其也被称为参考线(Reference Line),读者请注意区分参考线与车道线,车道线其实是指车道两侧的分界线,是两条;参考线可以取为车道线边界围成区域的中心线,是一条。在轨迹规划之前要先生成参考线,那么参考线是怎么来的呢?一般是先根据起点和目标点进行路线规划,根据路线经过的道路从高精地图中查找对应的道路中心线或者边界线,将所有道路的道路中心线拼接起来并进行光滑处理,防止出现间断或者跳变,因为一旦有不连续或者不光滑就会导致Frenet坐标系的不连续。这样就得到了一条光滑的参考线。
2.5 为什么用多项式?
无人车轨迹规划的目的就是得到一条曲线。为了在计算机中处理,这条曲线就必须可以方便地描述,这样一来我们可选的曲线并不是非常多,常用的有B样条曲线、Bezier曲线、Dubins曲线等等。我们在初中就已经认识多项式了,可以说是老熟人了,对它的性质也比较熟悉。比如,大名鼎鼎的泰勒公式就告诉我们,光滑的函数可以用很多个多项式来近似表示。这里说的多项式是指像这样 y ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 + a 5 x 5 y(x)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5} y(x)=a0+a1x+a2x2+a3x3+a4x4+a5x5 的一元幂次多项式。那么用几次多项式好呢?如果画出函数的图像,多项式其实也是一种曲线。跟前面这些曲线相比,多项式的形式更简单,无论是求导还是积分都比较容易。所以,为什么不试试用多项式来表示无人车的轨迹呢?显然论文作者就是这么考虑的。如果次数太少,曲线的表达能力不足,给不出我们想要的形状,如果次数太多,曲线过于扭曲,也不容易求解。经过仔细的思考,作者提出使用4次和5次这两种多项式。为什么选择这两种?作者给出了理由。首先,决定车辆乘坐舒适与否的指标不是速度、也不是加速度、而是取决于加加速度(英语叫Jerk)。根据最优控制的原理,对曲线上的加加速度进行积分,积分值最小的曲线刚好就是5次多项式。其次,5次多项式有6个待定系数,如果给定3个初始时刻的位置、速度、加速度三元组和终止时刻的三元组这六个已知量,刚好可以求出6个待定系数从而完全确定这个5次多项式。当然,有时我们不关心终止时刻的速度,所以有时也用4次多项式。
2.6 Frenet坐标系与笛卡尔坐标系的转换
轨迹规划出的曲线是叠加在Frenet坐标系下的结果。而计算轨迹的最大速度、判断有没有碰撞这些操作显然必须要在全局世界(笛卡尔)坐标系中进行,所以不可避免要在这两个坐标系之间转换。转换的方法如下:
1 Frenet → \rightarrow →Cartesian:即已知 ( s , d ) (s,d) (s,d)坐标计算 ( x , y ) (x,y) (x,y)坐标。这个计算简单,假设我们知道道路参考线的参数方程(用弧长参数化表示的),是用弧长 s s s作为自变量,参考线的 ( x r , y r ) (x_r,y_r) (xr,yr)坐标作为 s s s的函数,即 x r = x r ( s ) , y r = y r ( s ) x_r=x_r(s),y_r=y_r(s) xr=xr(s),yr=yr(s)。根据 s s s算出参考线的 ( x r , y r ) (x_r,y_r) (xr,yr)坐标,再对样条曲线求导算出 ( x r , y r ) (x_r,y_r) (xr,yr)处参考线的单位切线,再逆时针旋转 90 ° 90 \degree 90°得到单位法线向量 n n n,所以最终 ( x , y ) = ( x r , y r ) + d n ⃗ (x,y)=(x_r,y_r)+d\vec{n} (x,y)=(xr,yr)+dn ;
2 Cartesian → \rightarrow →Frenet:即已知 ( x , y ) (x,y) (x,y)坐标计算 ( s , d ) (s,d) (s,d)坐标。这个问题不容易,相当于在曲线上找到一个点,使得它离曲线外面一个固定点的距离最小。当然,如果这个曲线非常扭曲,找起来确实很难。但是如果曲线(参考线)是通过三次样条曲线插值离散参考点得到的,所以它就是个三次多项式,而且我们假设每两个参考点之间一段的曲线要么是直线要么是凸的,不会出现两次扭曲。当参考点取的足够密时,这样的假设是合理的。所以现在曲线的形式简单了,这样我们可以通过解方程求出这个点。
假设曲线外的点的坐标是 ( p x , p y ) (p_x,p_y) (px,py),三次曲线方程是 y = a x 3 + b x 2 + c x + e y=ax^3+bx^2+cx+e y=ax3+bx2+cx+e,点到曲线的距离平方如下(记为 g ( x ) g(x) g(x)):
g ( x ) = ( x − p x ) 2 + ( a x 3 + b x 2 + c x + e − p y ) 2 g(x)=(x-p_x)^2+(ax^3+bx^2+cx+e-p_y)^2 g(x)=(x−px)2+(ax3+bx2+cx+e−py)2
其中唯一的未知量是 x x x,所以我们求 g ( x ) g(x) g(x)的导数,并令其等于0即可。求出的点最多有五个,但是前面假设曲线只有一个弯曲的方向(三次项的系数 a = 0 a=0 a=0),所以实际最多三个点,我们挑出距离最小的那个即可。
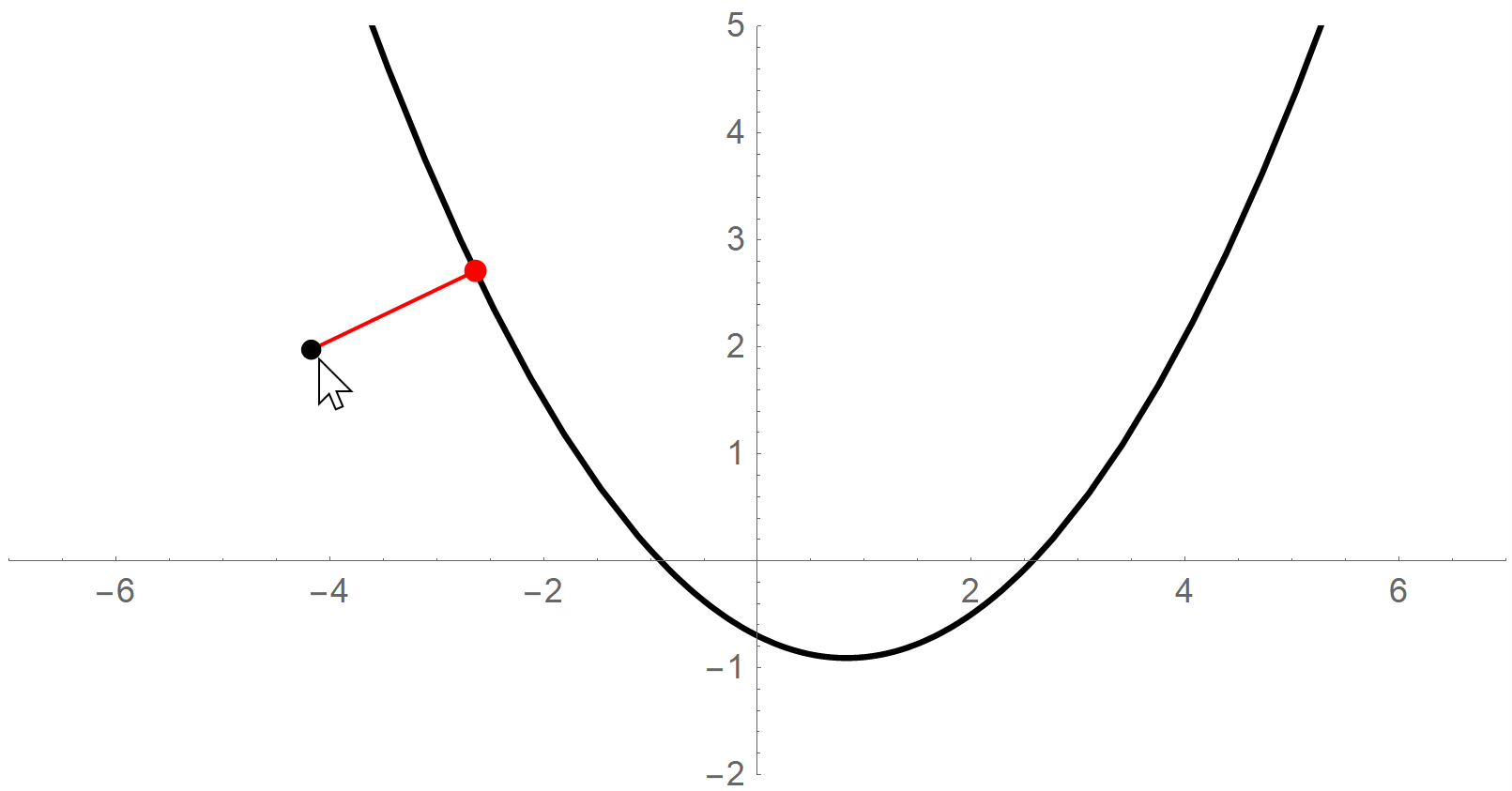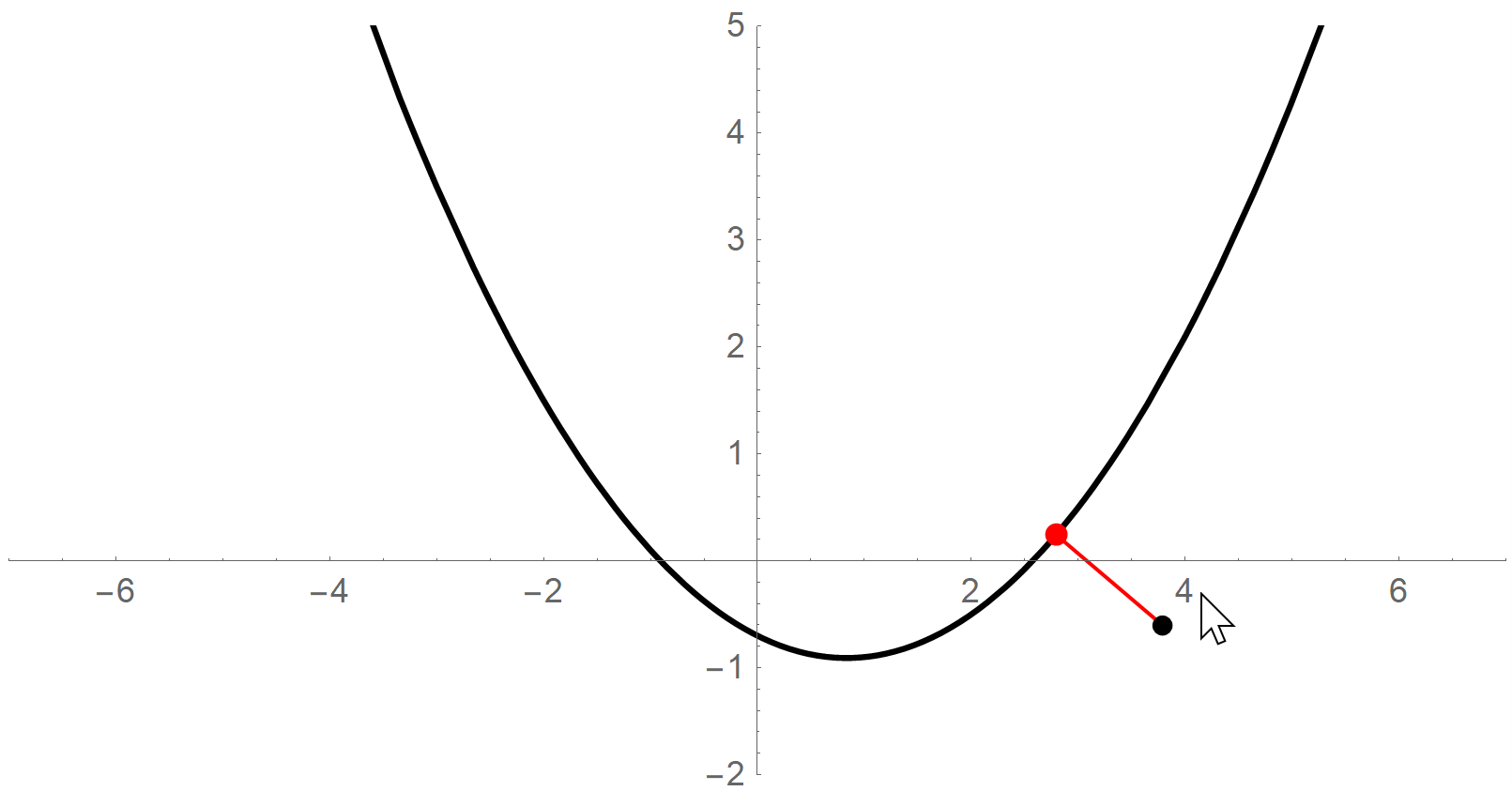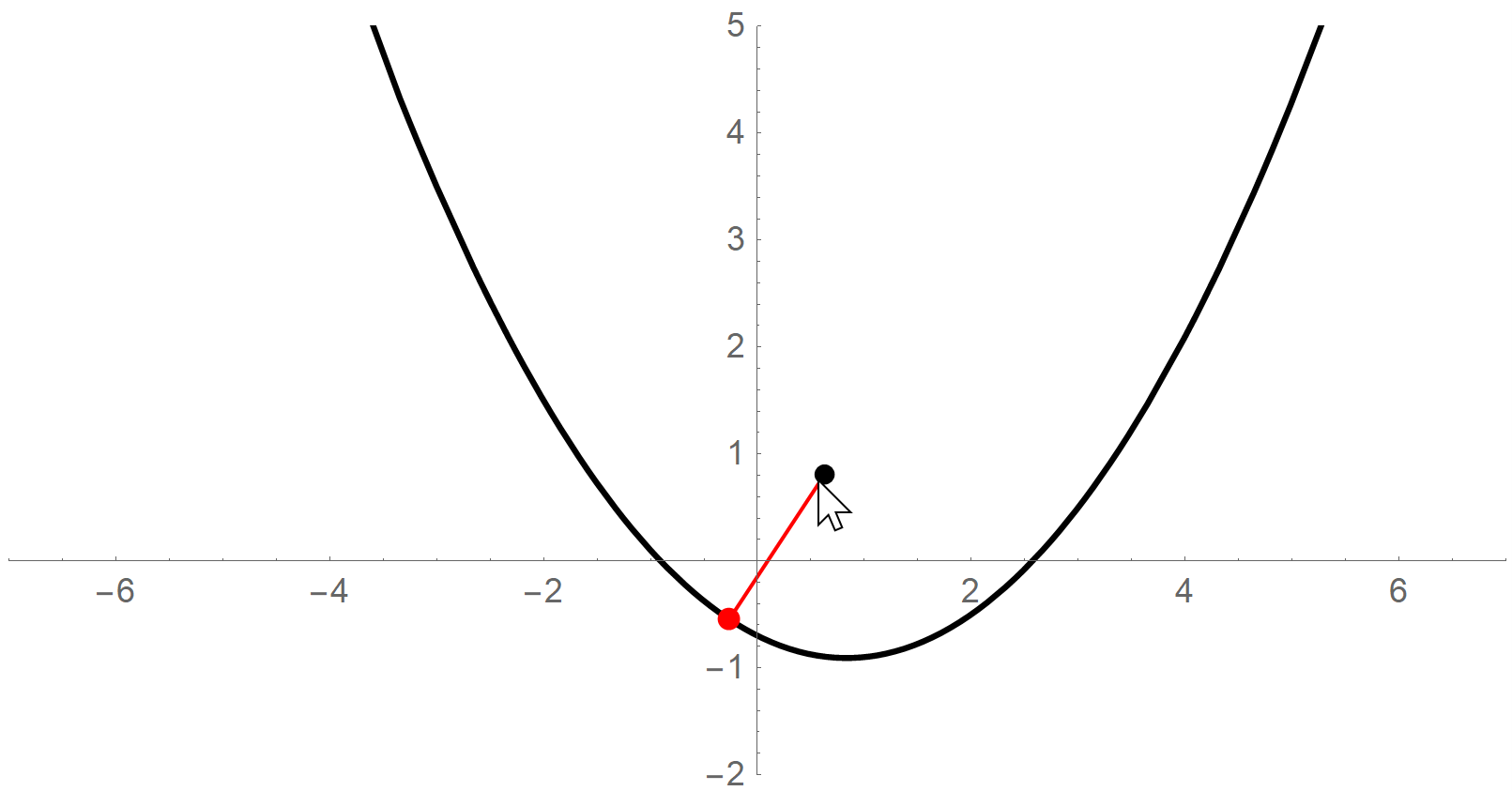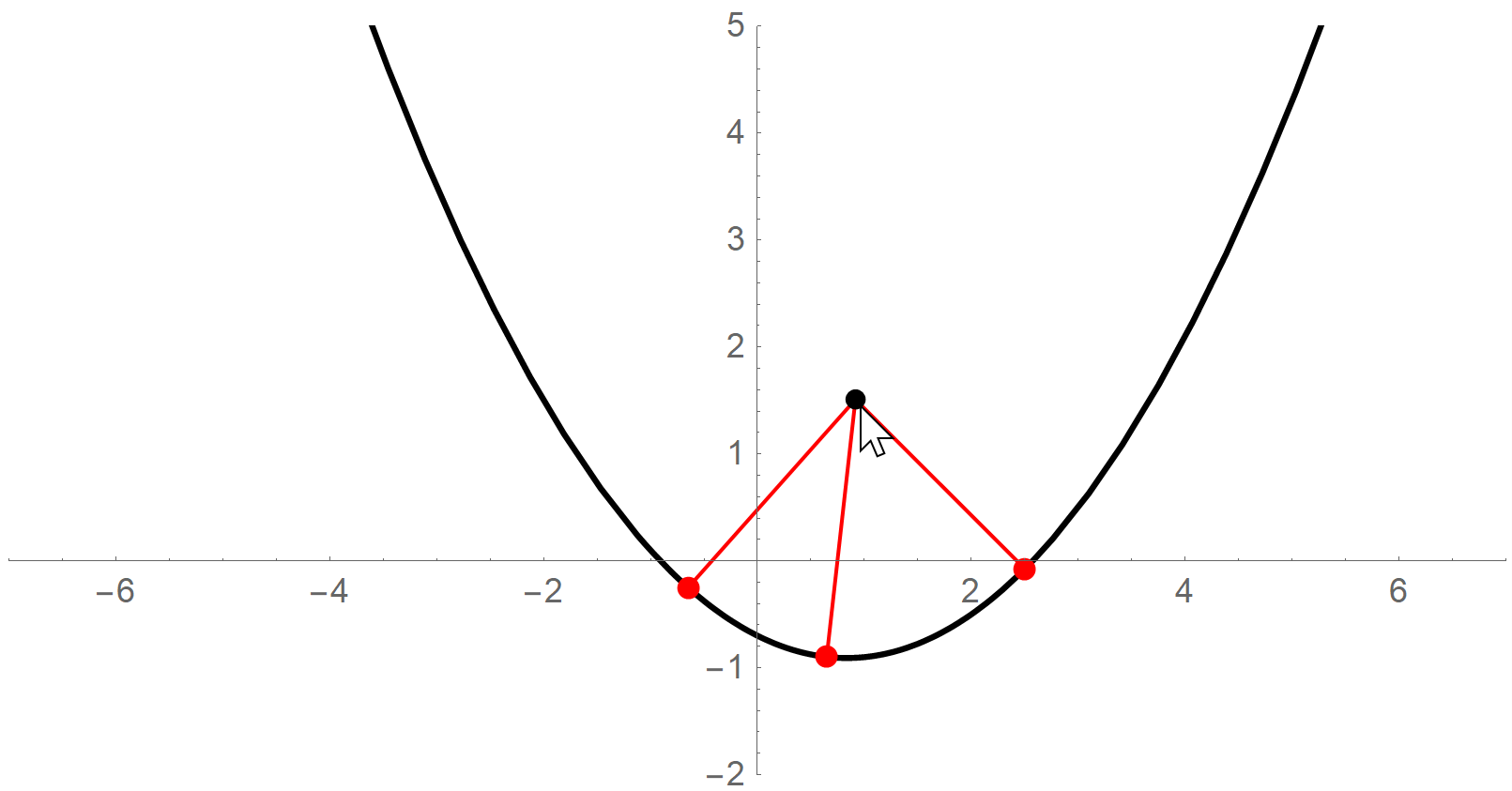
注意,弧长 s s s总是正的(我们假设车辆不能逆行或者倒车),但是 d d d可以是负的,道路左侧可以定义成 d > 0 d>0 d>0,右侧可以定义成 d < 0 d<0 d<0。
在百度Apollo无人驾驶项目中,这二者的转换函数在modules\common\math路径下的cartesian_frenet_conversion.cc文件。但是cartesian_to_frenet函数只是把 d d d算出来了,而最难的 s s s没算(直接作为已知输入)。注意百度把 ( s , d ) (s,d) (s,d)坐标记为 ( s , l ) (s,l) (s,l)坐标,这是因为符号 d d d被用于表示求导,防止弄混。
JMT函数中的polyeval(s0,T)是什么意思?polyeval是求多项式在某点的所有导数。这里的多项式是由系数s0定义的,s0是个状态类,它其实是 ( s 0 , s ˙ 0 , 1 2 s ¨ 0 ) (s_0,\dot s_0,\frac{1}{2}\ddot s_0) (s0,s˙0,21s¨0)。所以对应的多项式就是按照系数从低到高: f ( t ) = s 0 + s ˙ 0 t + 1 2 s ¨ 0 t 2 f(t)=s_0+\dot s_0t+\frac{1}{2}\ddot s_0t^2 f(t)=s0+s˙0t+21s¨0t2。这时再经过polyeval得到的输出就是三个导数项:零阶导数 s 0 + s ˙ 0 T + 1 2 s ¨ 0 T 2 s_0+\dot s_0T+\frac{1}{2}\ddot s_0T^2 s0+s˙0T+21s¨0T2、一阶导数 s ˙ 0 + s ¨ 0 T \dot s_0+\ddot s_0T s˙0+s¨0T、二阶导数 s ¨ 0 \ddot s_0 s¨0。
所以B就是两个三维状态向量之差:
s 1 − ( s 0 + s ˙ 0 T + 1 2 s ¨ 0 T 2 ) s ˙ 1 − ( s ˙ 0 + s ¨ 0 T ) s ¨ 1 − s ¨ 0 s_1-(s_0+\dot s_0T+\frac{1}{2}\ddot s_0T^2) \dot s_1-(\dot s_0+\ddot s_0T) \ddot s_1-\ddot s_0 s1−(s0+s˙0T+21s¨0T2)s˙1−(s˙0+s¨0T)s¨1−s¨0
generate_函数代码比较多,既然多我们就切成几部分来看。首先第一部分生成所有侧向轨迹,第二部分自然而然就是生成所有横向轨迹。第三部分则是将前面两部分的轨迹组合得到完整的轨迹,然后再根据代价从小到大排序,最后剔除掉可能碰撞的轨迹,最后剩下的最小轨迹就是输出的轨迹。
两个向量的叉积可以用来判断一个向量在另一个向量的那一侧,叉积的赋值是夹角的正弦。
{v1,v2}=m=RandomReal[{0,1},{2,2}];
ArcSin[Det[m]/Norm[v1]/Norm[v2]]
VectorAngle[v1,v2]
Graphics[{Arrow[{{0,0},v1}],Red,Arrow[{{0,0},v2}]},PlotRange->2]
3 行为决策
行为决策的意思是无人车应该采取什么行为,例如是变道还是停车。作者将所有可能的行为总结为4类:纵向方向的模式分别是Following,Merging,Stopping和Velocity Keeping。注意这里只提到纵向方向(也就是纵向 s s s坐标维度)。至于变道还是不变道则由侧向方向决定。侧向方向可以通过采样不同的侧向位置实现。此外,受到5次多项式本身表示能力的限制,规划出来的轨迹只能实现有限的行为,例如可以实现变道,但是无法生成连续的变道再回到原来车道的一段轨迹。
根据末端状态,前三种Following,Merging,Stopping可以归为一类,Velocity Keeping单独归为一类。为什么呢,因为前三种都需要限制轨迹末端的位置、速度和加速度,而Velocity Keeping只需要限制末端的速度和加速度,对位置不限制。从多项式函数的角度看,前三种用5次多项式表示,后一种用的是4次多项式。所以在代码中定义了following_merging_stoping函数统一处理。对于侧向方向不作分类,总是5次多项式,因为我们一定要约束侧向方向的末端位置在车道某处,而不希望无人车自由发挥。在实际应用中,笔者认为Merging遇到的情况不多,所以暂时不考虑,本文也不过多讨论。对于Following和Stopping来说,我们都要明确知道前车的状态(主要是位置和速度)。作者只考虑了Following,Merging和Velocity Keeping。Merging出现最少,只出现了2次。Following和Velocity Keeping分别都出现了5次。
下面重点分析Following和Stopping。
Stopping:在原程序中,作者没有考虑Stopping这种情况(所以TrajectoryGenerator.h中的stopping函数始终没被调用过)。当然这也是有道理的,因为无人车在正常执行任务时,我们希望Stopping最好不要出现,除非遇到特殊情况不得不停车,这时无人车可能无路可走了。
Following:跟车时,我们最关心的决策信息是被跟随者的位置和速度。首先,被跟随者必须在无人车的前方,如果被跟随者与无人车齐头并进或者在无人车后面,那显然无人车不能跟随它。如果只考虑速度还不够,如果被跟随者的速度为0甚至为负,那么无人车显然应该避让,不能再跟随。所以跟随模式的条件可以设计成下表这样的形式。其中, s c s_c sc是被跟者的纵向位置, s e s_e se是无人车的纵向位置, v c v_c vc是被跟者的纵向速度。只有当间距足够大和速度足够快同时满足,无人车才会考虑跟车。
BehaviorModule.h文件,其中Search_Center函数用于搜索无人车自己所在车道的情况,并以此进行决策,决定是采用FOLLOWING还是VELOCITY_KEEPING亦或MERGING。决策过程的判断逻辑是如下:
首先,查看目标车道Goal_Lane的前后有没有其它车辆,分成两种情况:
1 前面有车,此时根据后面有没有车再分成两种情况:
1.1 后面有车,此时计算前后车的间距,称为自由空间free_space。如果自由空间比Max_Tight_Merge_Offset大,再看与汽车的距离nf,如果nf小于Consider_Distance,则采用FOLLOWING模式, 采用前车的速度跟车行驶。如果nf不小于Consider_Distance,则采用VELOCITY_KEEPING模式,以v_ref参考速度速度保持。如果自由空间不比Max_Tight_Merge_Offset大,而是只比Min_Tight_Merge_Offset大,说明自由空间不宽裕,此时采用MERGING模式,保持在前后车中点位置行驶。如果自由空间比Min_Tight_Merge_Offset还小,此时不管,该情况应该是危险的特殊情况,应该单独考虑。
1.2 后面没车,此时如果无人车与前车的距离小于Consider_Distance,则采用FOLLOWING模式, 采用前车的速度跟车行驶。如果与前车的距离大于Consider_Distance,则采用VELOCITY_KEEPING模式,以恒定的v_ref参考速度。
前面有车时还做了一件事,就是看前车的车速,如果车速小于v_ref,说明前车太墨迹开得太慢,那么就要考虑变道超车,将变道超车的标志位attempt_switch置为true。
2 前面没车,以v_ref参考速度速度保持。此时不管后面有没有车,后面有车也不理它。
乍一看,上面的模式好像很多,有些复杂,但是实际上这些条件判断都是排他性的,所以最后只能有一种模式被选中,不会同时选择多个。最后把搜索模式和attempt_switch返回。
如果后方来车比较快,无人车应该怎么反应?
4 代码分析
最核心的PlanPath函数主要起到行为决策的功能,它只有两个输入,无人车自身的实时信息ego(包括尺寸、状态、轨迹)和无人车附近的其它车辆near_cars的信息。注意它除此以外没有接收其它信息,所以这个函数只能无休止的跑下去,而不能达到某个期望的目标位置,这显然是需要改造的。我们先分析PlanPath函数的功能:
1 首先,根据无人车的横向距离计算所在车道ego_lane,再计算无人车的纵向速度ego_speed。再有就是设定无人车的参考车速v_ref,这是非常重要的部分,笔者认为这部分不应该藏在这里,而是应该作为输入参数,因为我们可能会经常根据环境和任务调整这个参考速度。
2 随后,从其它车辆near_cars中提取其它的信息,例如每辆车所在的车道、和无人车的间距、预测的纵向车速等等。
3 最后也是最重要的部分,就是利用前面提取的信息搜索行为模式了。为了表示模式,作者定义了SearchMode和ActiveMode结构体。搜索出行为模式后,后面的函数会从这两个结构体中提取出行为类型和与这种行为有关的参数,例如目标速度、前车的状态等等,进行具体的轨迹生成。所以为了理解后面的程序,就要先了解这两个结构体的定义。
ActiveMode结构体中定义了三个成员,如下:
① 具体的行为模式(Following,Merging,Stopping,Velocity Keeping其中的一种)
② 其它车辆的状态,包括无人车前方和后方的车辆
③ 数字。最后这个数字number有两个模式会使用到,分别是停车和速度保持,当然对应的含义也不一样。对于停车模式,number存储的是应该停车的目标位置(纵向位置s);对于速度保持,number存储的当然就是目标车速了(纵向速度)。这些在TrajectoryGenerator.h文件中的generate_函数中可以根据函数调用很容易猜出来。
struct ActiveMode {
Mode mode;
vector<State> state;
double number; };
SearchMode结构体中也定义了三个成员,分别是:
① ActiveMode结构体 你可能注意到了,activeModes不是一个,而是一个向量,也就是说SearchMode结构体可以存储不只一个ActiveMode结构体。那么对于多个SearchMode结构体,它们中的具体模式有没有可能重复呢,不排除这种可能。
② 目标车道 每个SearchMode只存储一个目标车道。
③ 最小前车速度 min_lv_speed只在BehaviorModule.h文件中使用,其它文件中没有见到使用。min_lv_speed用来计算轨迹的代价。
struct SearchMode {
vector<ActiveMode> activeModes;
double goal_lane;
double min_lv_speed; };
4.1 多项式函数库polynomial.h
文件polynomial.h包含一系列与多项式有关的函数,例如相乘、求导等,其命名与MATLAB一样。polyval函数的作用是计算某个(x)值处的多项式函数值(y(x)),其定义如下。MATLAB也有同名函数。
/* polyval : evaluate a polynomial at xi */
double polyval(VectorXd const& coef, double xi) {
int N = coef.size();
if (N==1) return coef(0);
double yi = coef(N-1);
for (int i=N-2; i>=0; --i) {
yi = (yi*xi + coef(i));
}
return yi;
};
polyval函数的输入是定义多项式的系数coef和自变量取值x。系数coef的定义是低次项在前,高次项在后。我们举个例子,假设系数coef = {a, b, c, d};,那么x处的函数值是y(x) = a + b x + c x^2 + d x^3。在Mathematica软件中可以看到计算结果:
coef={a,b,c,d};
n=Length[coef];
y=coef[[n]];
For[i=n-1,i>=1,--i,y=(y*x+coef[[i]])]
y//Expand

另一个长得差不多的函数polyeval的功能是计算多项式在某点处所有的的导数。注意是所有的导数,包括0阶导数(就相当于计算函数值),以及无穷阶导数(超过次数+1以后都是零)。
VectorXd polyeval(VectorXd const& coef, double xi) {
int N = coef.size();
// Compute a factorial array and the powers of xi
VectorXd fac = VectorXd::LinSpaced(N,0,N-1);
VectorXd xip = VectorXd::Ones(N);
fac(0) = 1;
if (N>1) {
xip(1) = xi;
for (int i=2; i<N; ++i) {
fac(i) *= fac(i-1);
xip(i) = xip(i-1)*xi;
}
}
xip = xip.cwiseQuotient(fac); // xi^j/j!
VectorXd f = coef.cwiseProduct(fac); // a(j) * j!
VectorXd Ad = VectorXd::Zero(N);
// The n'th derivative at xi is a convolution between f and xip
for (int r=0; r<N; ++r) {
Ad(r) = f.tail(N-r).dot(xip.head(N-r));
}
return Ad;
};
PP的意思是分段多项式函数(Piece-wise polynomial),作者单独定义了一个类来表示该函数。具体来说,PP就是一个多次样条曲线,而PP2是PP的一个特例,是2段多次样条曲线。它们都在polynomial.h里,Trajectory类就是继承自PP2,说明它也是一个“2段多次样条曲线”,但是Vehicle中出现的Trajectory最多只使用二次样条,表示位置、速度和加速度,这是初始化时决定的。所以如果运行Vehicle中的display()会看到trajectory[0].display();只显示三个数值(代表多项式系数)。正常的四次或五次多项式则会显示5个或6个数值。
Trajectory() : PP2() {};
PP2() : coef({VectorXd::Zero(3)}), knot(1e300) {}
VectorXd::Zero(3) = {0,0,0}
4.2 Trajectory类
Trajectory类对两段分段多项式PP2类重新封装了一下,说白了就是用时间参数化的多项式来表示轨迹,这个轨迹可以是无人车本身的也可以是动态障碍物的。既然用时间参数化了,那就可以取出某个时刻物体(例如无人车)的状态,这里的状态具体指的是:位置、速度、加速度,程序中用Vector3d类型表示。注意一个轨迹Trajectory只是针对一个维度,而我们的物体用一个维度是不能确定的,必须用两个维度(就是对应Frenet坐标系的s维和d维)。所以在Vehicle类中定义了二维轨迹向量:vector
4.3 车辆类型
该程序定义车辆为Vehicle类,不管是无人车还是其它障碍物车辆都用一个类表示。如果再扩展一些,这个类也是对静态和动态物体的统一表达,因为静态可以被视为动态的特例,当然行人、自行车也可以使用这个类来表示。Vehicle中存储着车辆的以下信息:
① ID标示
① 形状信息,将车辆用长方形表示,需要定义长和宽
① 状态信息,即位置、速度、加速度
① 轨迹信息,这个表示未来一定时间车辆可能的状态。
正因为有轨迹信息,所以支持对动态物体进行避障。碰撞检测函数是helpers文件中的overlap函数。compute_2d_validity函数遍历不同时刻无人车和障碍物的位置并调用overlap函数进行碰撞检测。
4.4 车道参考线
参考线的制作调用了第三方spline.h文件,方法是对一些离散的点进行分段三次样条插值,得到一段段连续的解析曲线。RoadMap.h文件用于定义与参考线有关的计算函数,例如从frenet坐标转换为直角坐标,这个函数就是getXY。
定义参考线所需的离散点被弧长参数化,其格式如下。
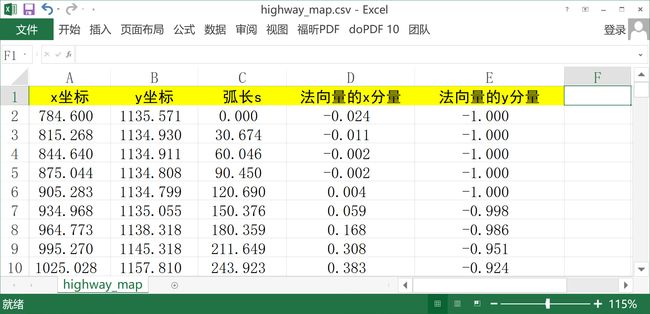
如果在数学计算软件中显示出来就是下图这样的,红色的箭头就是法向量,每个点处都有一个。
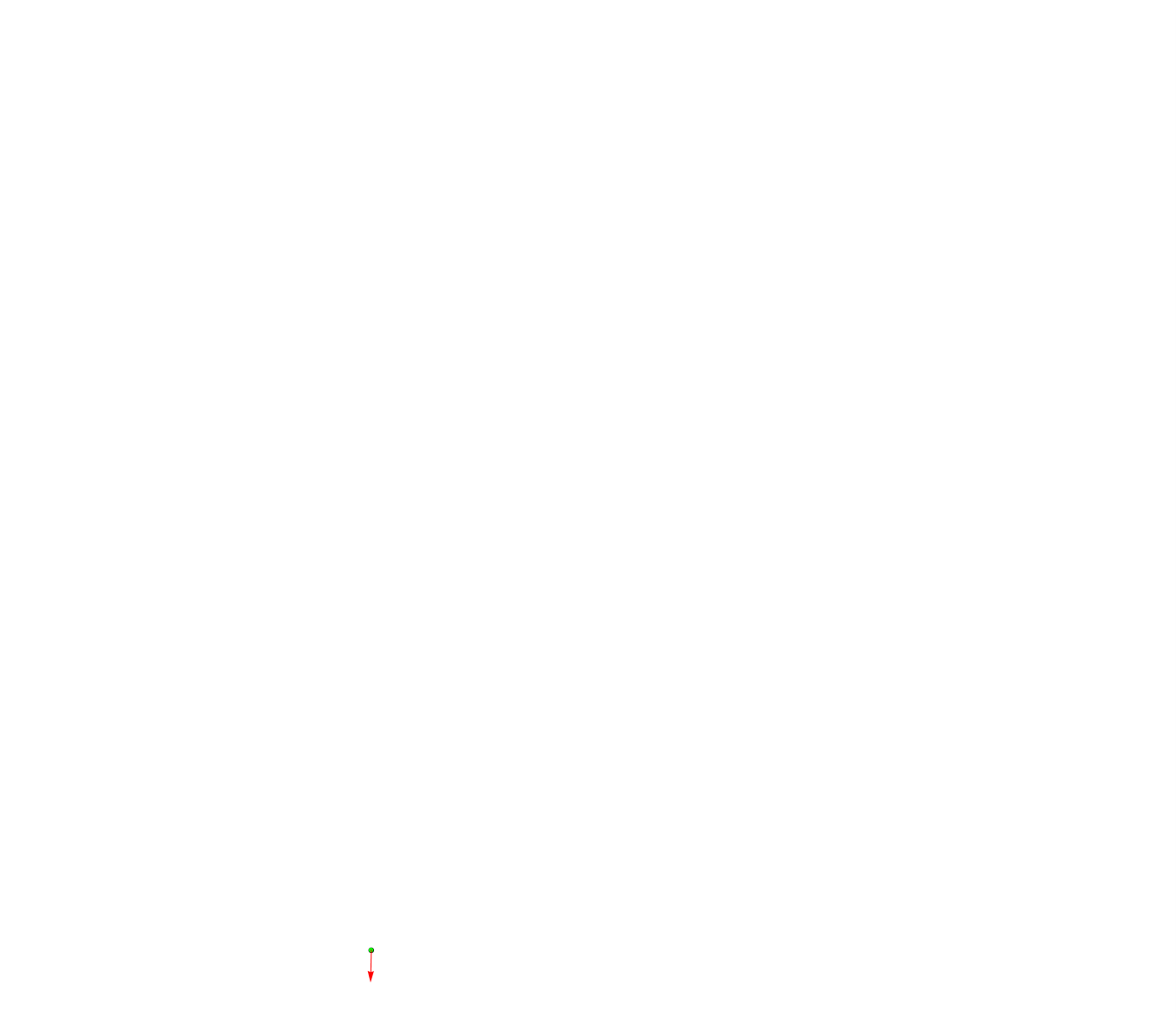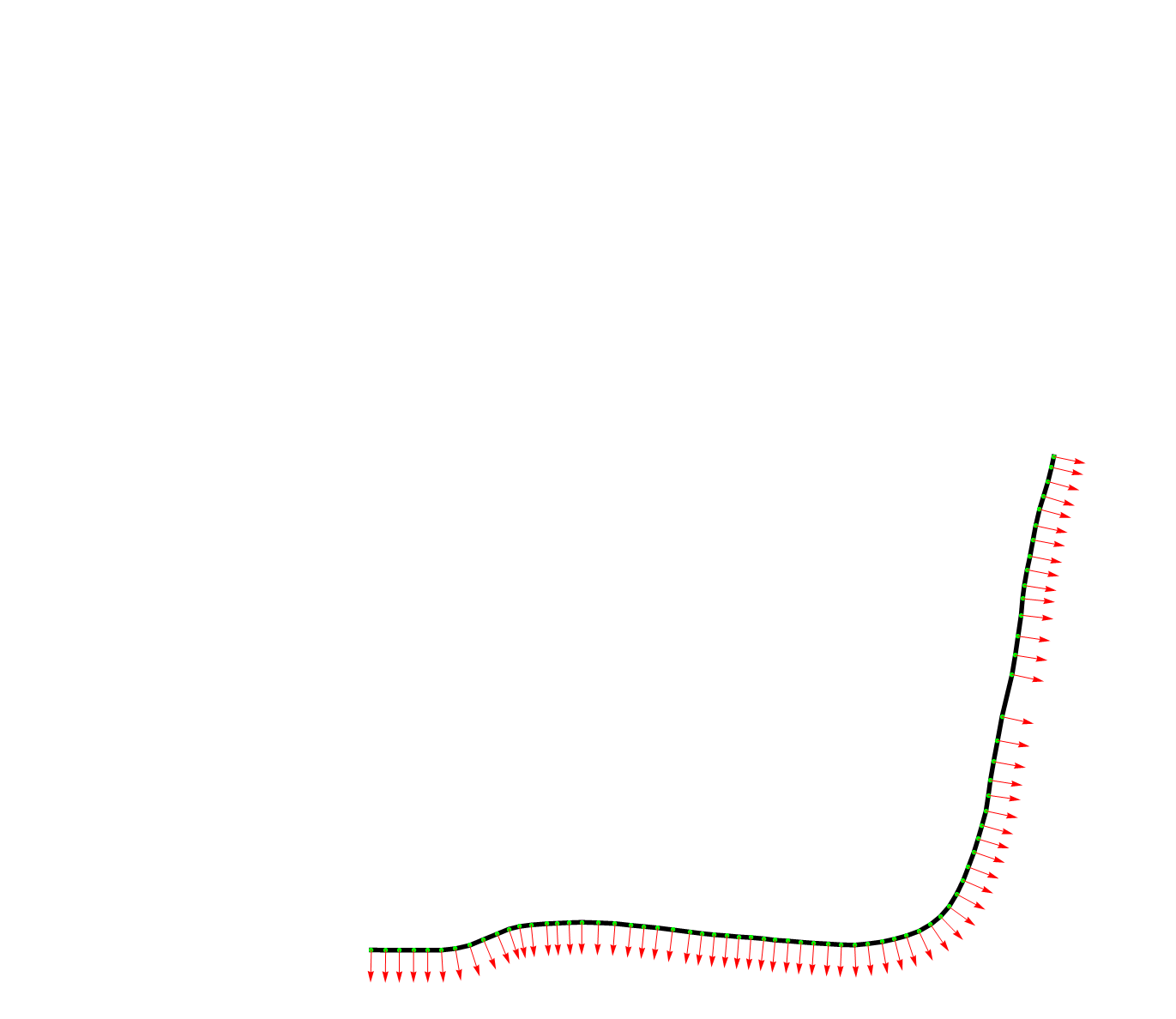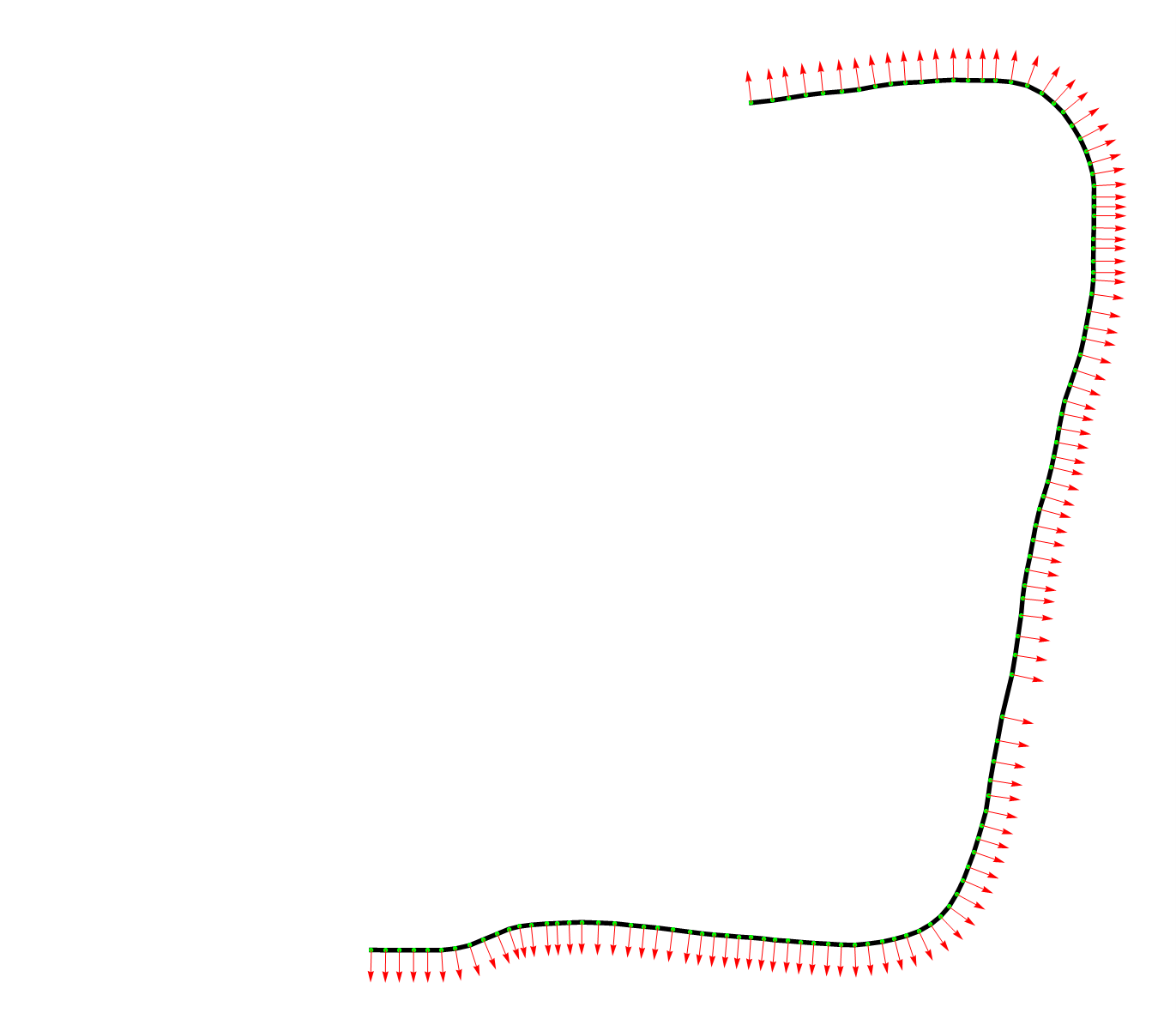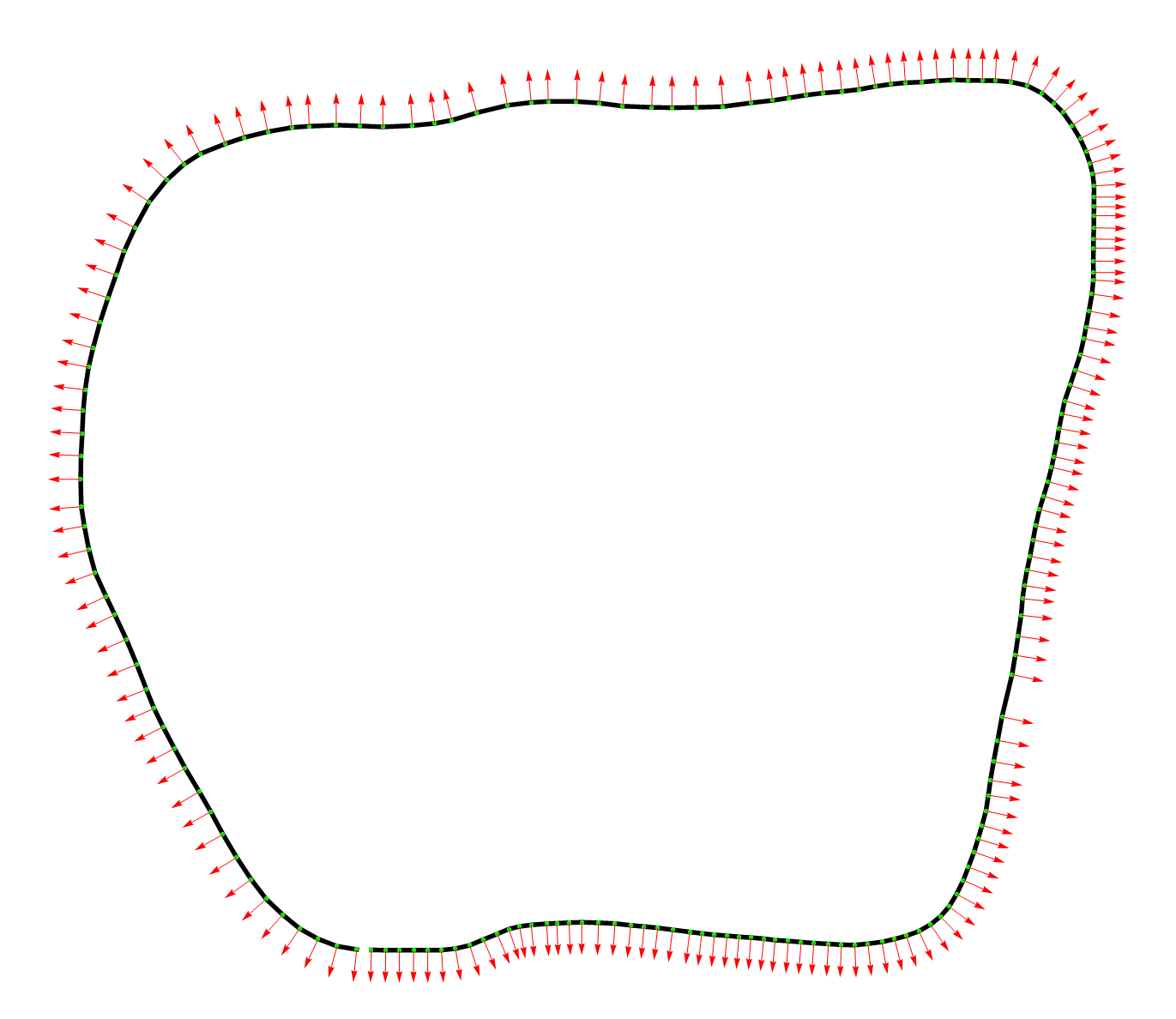
参考线应该怎么生成这个问题没有唯一答案。参考线可以位于道路中心,也可以位于道路最左侧或者最右侧,随你的习惯而定。不过原程序中默认是位于最左侧的,即无人车总是在参考线右侧行驶。如果想把参考线定义成成最右侧,可以改变getXY函数里的法向量的方向,加个负号即可,其它地方不用改。
// road normal vector
Vector2d n;
n << t(1), -t(0);
r += -d*n; // 原来是r += d*n;
5 常见问题
5.1 轨迹如何拼接?
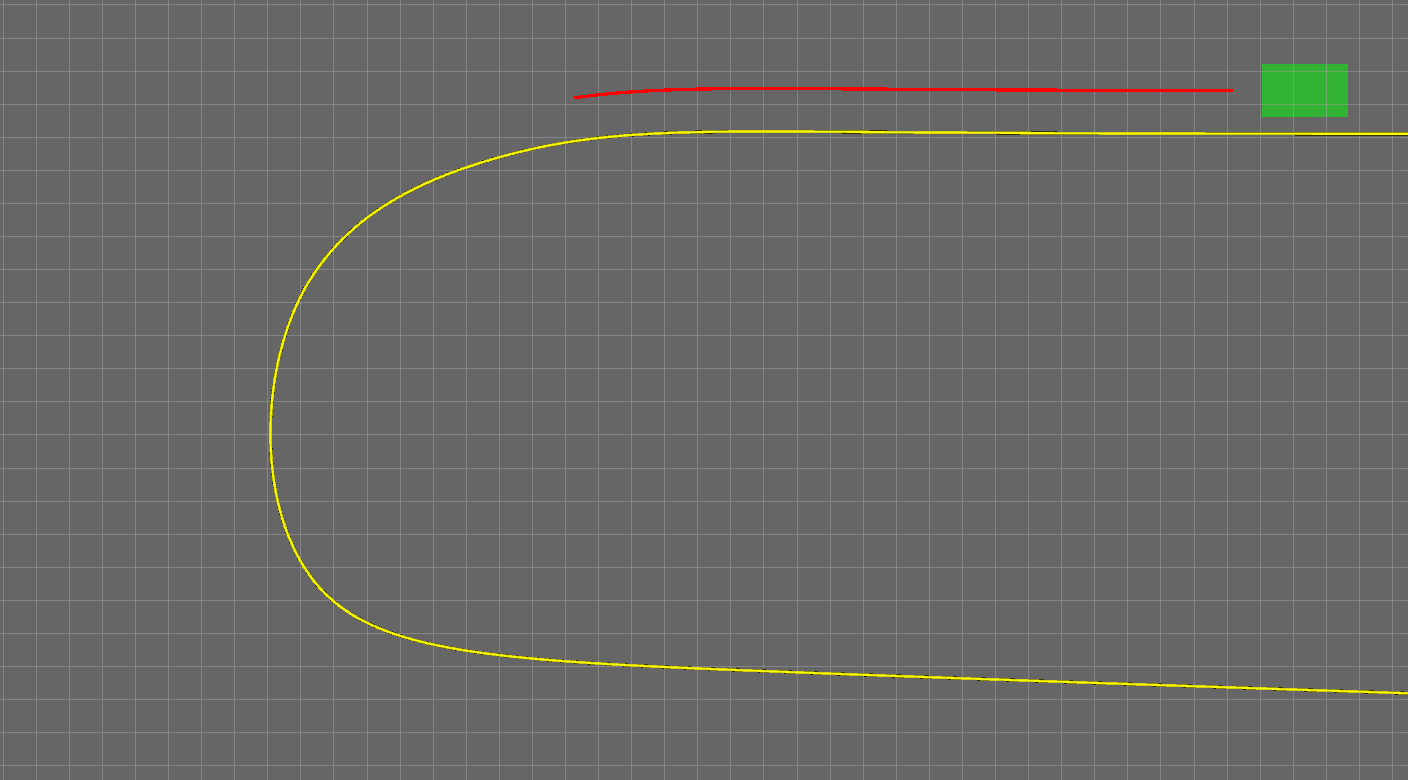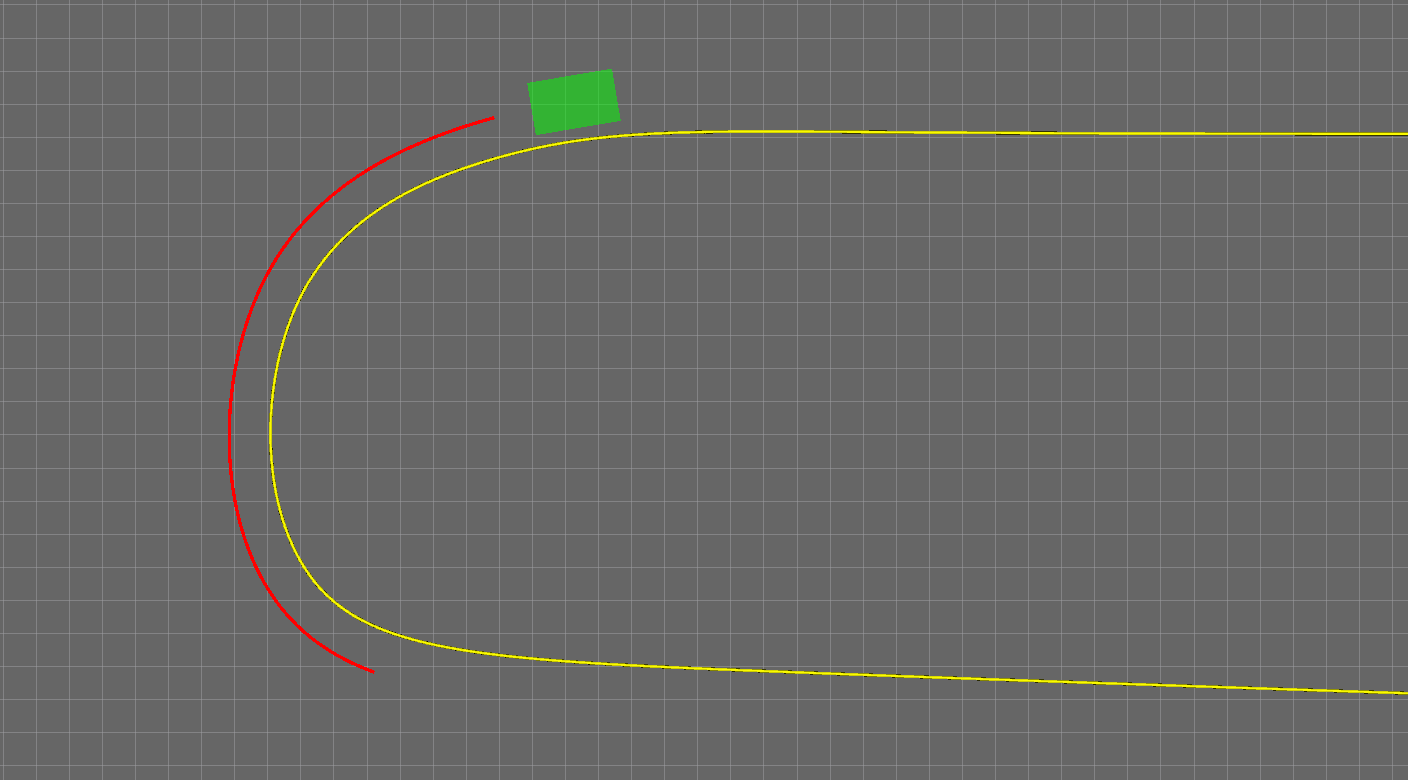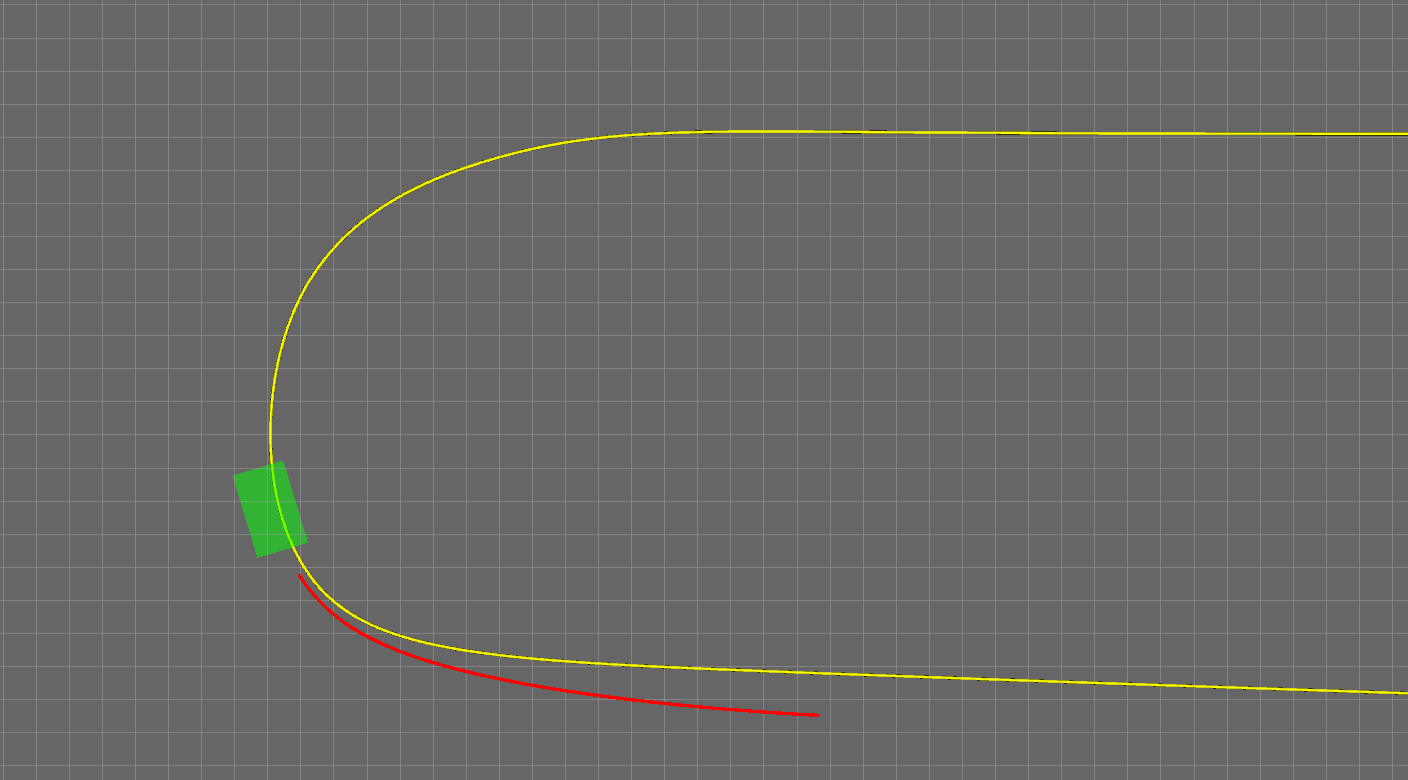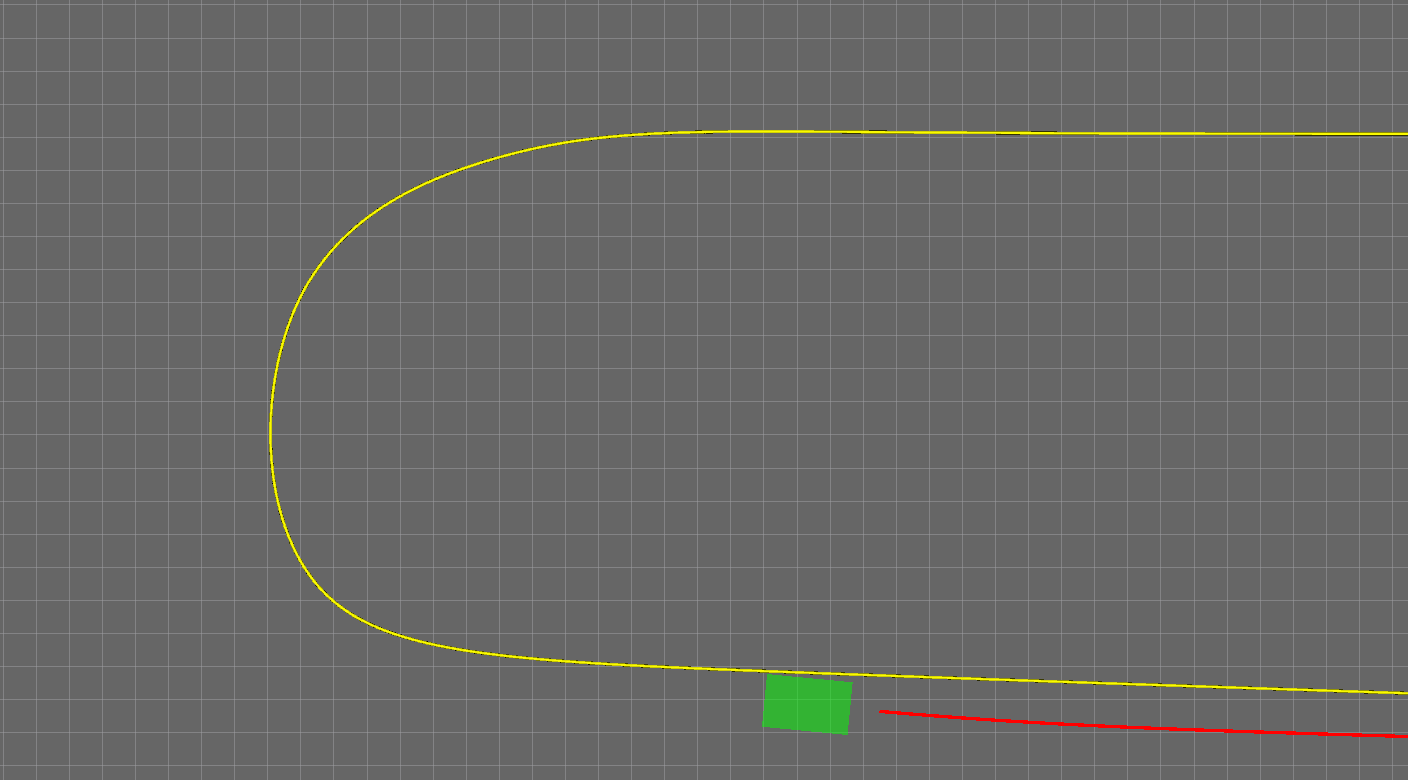
无人车在规划时是定时触发的,也就是按照固定的时间间隔(比如0.1秒)重复运行规划程序不断更新轨迹。这自然就带来一些问题,一个问题是下一次的规划的起点如何确定。如果起点选择的不好,那两段轨迹有可能过渡的不好,导致轨迹断裂、不光滑等等问题。所以起点如何选择,大多数人想当然的第一反应是:当然是规划当前时刻无人车实时的位置和速度了。但这会产生一个严重的问题,如下图所示。黄色线是参考线,红色曲线就是规划的轨迹。在拐弯的时候,无人车逐渐偏离了参考线甚至与参考线产生了交叉,而我们并没有让无人车变道,这显然不是我们想要的。为什么会出现这个问题呢?原因是无人车在跟踪参考轨迹时是滞后于轨迹的,如果每次都是以无人车当前时刻的状态作为起点来规划下一次的轨迹,那控制模块就会与规划模块形成耦合,使整个系统产生滞后,就会产生轨迹被车辆推着走的现象。所以,在设置规划的起点时一定要小心。解决方法就是,每次规划的起点是上一次规划的轨迹上的一部分,笔者选择的是上一次轨迹上离无人车最近的那个点的状态。
6 在Rviz中显示
开源项目SDC_ND_T3P1_Path_Planning是Udacity推出的自动驾驶课程系列的衍生代码,同时也提供了车辆运动的模拟器,能够仿真可视化。关于项目如何运行起来,这篇文章说的很清楚了。关于模拟器介绍几点。模拟器叫Udacity Self-driving Car Simulator,是Udacity的纳米学位课程中搭建的教学软件,使用Unity 3D游戏开发软件制作,界面如下右图。其中的黑车是无人车,车前的绿色线条就是规划出来的轨迹。模拟器是开源的,这篇文章提到,模拟器是用Unity 3D V5.5.1f1版本开发的,不要使用过高版本打开,因为老版本中的有些函数新版本并不支持。模拟器可以点击这里下载。但是笔者发现,有些资源(png材质)被禁止下载了,就算你安装了大文件版本git lfs或者fork到自己的仓库或码云也不行。因为作者加了限制,只有企业版才有下载权限。这就导致无法再在Unity中修改。此外模拟器运行起来很耗资源,而且每次启动之后其它车辆的位置都是随机的,无法复现bug。所以我放弃了使用模拟器而采用ROS的Rviz作为可视化界面。
利用Rviz发送障碍物,演示避障。
演示停车。
7 踩过的坑
7.1 C++编程
7.1.1 在一个构造函数里调用另一个构造函数
第一个大坑是关于构造函数调用的,这个问题有人遇到过:C++中可以在构造函数中调用另一个构造函数吗?
下面这样直接调用是不可以的,编译不会报错,但是一旦运行就有问题。
Vehicle::Vehicle(int id)
{
Vehicle(id, length, width);
}
但是写成这样是可以的,运行没有问题。
Vehicle::Vehicle(int id) : Vehicle(id, length, width, 0) {};
7.1.2 函数的默认输入
如果函数有默认的输入,声明和实现都要写。
头文件中写声明,注意C = 0:
VectorXd polyint(VectorXd const& coef, double C = 0);
cpp文件写实现:
VectorXd polyint(VectorXd const& coef, double C = 0) {
int N = coef.size();
VectorXd coefi = VectorXd::Zero(N+1);
coefi.tail(N) = coef.cwiseQuotient(VectorXd::LinSpaced(N,1,N));
coefi(0) = C;
return coefi;};
7.1.3 const
如果不想定义成类,那么成员变量怎么定义?在头文件中的变量定义时加上const修饰符即可,这样就能在cpp文件中使用了。
7.1.4 头文件中定义函数
头文件中不能定义函数,除非定义成内联函数或者加上const修饰符。