XGBoost入门了解

XGBoost入门了解

一 概念
XGBoost（Extreme Gradient Boosting）代表“极端梯度增强”，其中“梯度增强”一词来源于弗里德曼的论文《贪婪函数逼近：梯度增强机》,它可用于回归也可用于分类问题。

1、回归树与分类树 　
　事实上，分类与回归是一个型号的东西，只不过分类的结果是离散值，回归是连续的，本质是一样的，都是特征（feature）到标签/结果（label）之间的映射。
　分类树的样本输出是哪一类的形式，如判断蘑菇是有毒还是无毒，周末去看电影还是不去。而回归树的样本输出是数值的形式，比如给某人发放房屋贷款的数额就是具体的数值，可以是0到120万元之间的任意值。
　
　2、boosting集成学习　
　boosting集成学习，由多个相关联的决策树联合决策，什么叫相关联？举个例子，有一个样本真实情况是：[数据->标签]是[(2，4，5)-> 4]，第一棵决策树用这个样本训练得预测为3.3。那么第二棵决策树训练时的输入参考上一次的预测结果，这个样本就变成了[(2，4，5)-> 0.7]，也就是说，下一棵决策树输入样本会与前面决策树的训练和预测相关。(每棵树之间是串联的)。所以首先XGboost是一个boosting的集成学习。
　
二、 集成思想
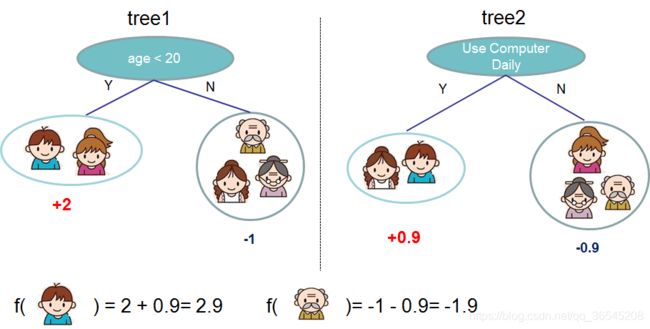
集成学习方法是指将多个学习模型组合，以获得更好的效果，使组合后的模型具有更强的泛化能力。XGBoost是以CART树(一堆二叉树)进行组合。故在此之前，我们先看下CART树。如下图，通过用户年龄进行判断用户是否喜欢玩游戏的得分值，得到一棵CART树模型。再由用户是否日常使用电脑判断用户是否喜欢玩游戏的得分值，得到另一棵CART树模型。
我们知道对于单个的决策树模型容易出现过拟合，并且不能在实际中有效应用。所以出现了集成学习方法。如下图，通过两棵树组合进行玩游戏得分值预测。其中tree1中对小男生的预测分值为2，tree2对小男生的预测分值为0.9。则该小男生的最后得分值为2.9。

将上面集成学习方法推广到一般情况，可知其预测模型为：

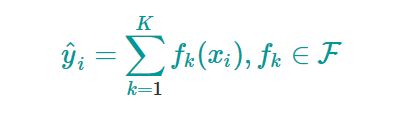
其中：

是K棵树对第i个样本的预测值。

K是现存K棵树，f是每棵树的结构，F是所有可能的树的集合(空间)。X是每个样本，x1是第一个样本，x2是第二个样本…，

那我们要的目标函数（现存K棵树，n个样本）即：

也就是说我们的目标函数（由K棵树组成的）由两部分构成：损失函数加正则项
其中：

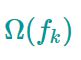
表示每棵树的正则项（惩罚项），我们现在只要知道它的作用是控制每棵树的复杂度，防止树的结构过于复杂导致模型泛化性变差即可。

表示每个样本的真实值与预测值之间的差值。

三、 XGBoost未知参数
上面，我们得到了XGBoost模型和它的目标函数，那么训练的任务就是通过最小化目标函数来找到最佳的参数组。

问题是参数在哪里？我们很自然地想到，XGBoost模型由CART树组成，参数自然存在于每棵CART树之中。

那么，就单一的 CART树而言，它的参数是什么呢？

根据上面对CART树的介绍，我们知道，确定一棵CART树需要确定两部分，第一部分就是树的结构，这个结构负责将一个样本映射到一个确定的叶子节点上，其本质上就是一个函数。第二部分就是各个叶子节点上的分数。
似乎遇到麻烦了，你要说叶子节点的分数作为参数，还是没问题的，但树的结构如何作为参数呢？而且我们还不是一棵树，而是K棵树!
让我们想像一下，**如果K棵树的结构都已经确定，那么整个模型剩下的就是所有K棵树的叶子节点的值.**此时，整个目标函数其实就是一个K棵树的所有叶子节点的值的函数。

四、 训练XGBoost
我们的目标不再是直接优化整个目标函数，这已经被我们证明是行不通的。而是分步骤优化目标函数，首先优化第一棵树，完了之后再优化第二棵树，直至优化完K棵树。整个过程如下图所示：

你可能还会问：我们每一步都想要哪棵树？一件很自然的事情是添加一个可以优化我们的目标函数的树。

即在第t步时，我们添加了一棵最优的CART树f，这棵最优的CART树f是怎么得来的呢？非常简单，就是在现有的t-1棵树的基础上，使得目标函数值最小的那棵CART树。
目标函数如下图：
其中我们是知道前t-1棵树的所有结构，才去构造第t棵树，所以前t-1棵树的正则项我们都是知道的，故变成了常数。
对于一般的损失函数，我们需要将其作泰勒二阶展开。

其中：

当我们再次把常数项都移除后变为：　　　　　　　　　　　　　　
其中：
之间的差值为常数去除了。

五、 正则项
我们先对CART树作另一番定义，如下所示：

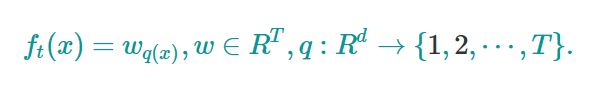
需要解释下这个定义，首先，一棵树有T个叶子节点，这T个叶子节点的值组成了一个T维向量w，q(x)是一个映射（函数），也就是把每个样本分到某个叶子节点需要这个q(x)做指点，q(x)其实就代表了CART树的结构。w_q(x)自然就是这棵树对样本x的预测值了。
而XGBoost就使用了如下的正则化项（人家自己定义的）：

其中γ和λ，这是XGBoost自己定义的，在使用XGBoost时，你可以设定它们的值，显然，γ越大，表示越希望获得结构简单的树，因为此时对较多叶子节点的树的惩罚越大。λ越大也是越希望获得结构简单的树。w是每个叶子节点的权重，也就是得分。T是f这棵树的叶子节点数。

那么我们把上面的目标函数再次化为：

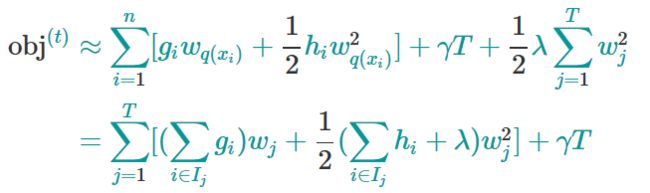
这里需要停一停，认真体会下。Ij代表什么？它代表一个集合，集合中每个值代表一个训练样本的序号，整个集合就是被第t棵CART树分到了第j个叶子节点上的训练样本。理解了这一点，再看这步转换，其实就是内外求和顺序的改变。

然后令：


则目标函数变为：

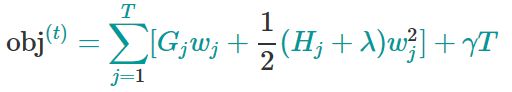
我们发现最后的目标函数实际上就剩下第t棵树了，对于第t棵CART树的某一个确定的结构，所有的Gj和Hj都是确定的。而且上式中各个叶子节点的值wj之间是互相独立的。上式其实就是一个简单的二次式，我们分别对各个叶子节点的权重求偏导，很容易求出各个叶子节点的最佳值以及此时目标函数的值。如下所示：

obj*代表了什么呢？

它表示了这棵树的结构有多好，值越小，代表这样结构越好！也就是说，它是衡量第t棵CART树的结构好坏的标准。注意_注意注意~，这个值仅仅是用来衡量结构的好坏的，与叶子节点的值可是无关的。为什么？请再仔细看一下obj的推导过程。obj只和Gj和Hj和T**有关，而它们又只和树的结构(q(x))有关，与叶子节点的值可是半毛关系没有。如下图所示：

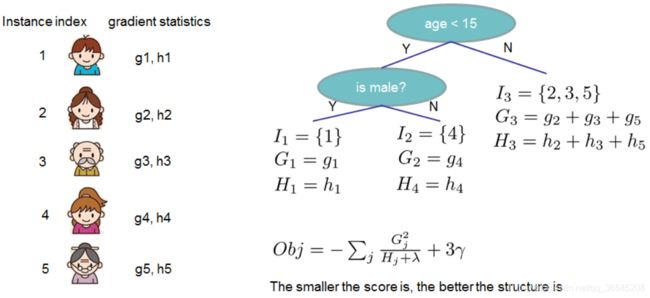
六、 找出最优树的结构
这里是什么意思呢？上面我们只是在通过建立K棵树来找一个评判标准，不能说随便拿个公式就可评判树的好坏吧。实际上这个算法在使用的时候只是构建一棵树，我们把原来那种构建多棵树的思想转换为一层层的构建节点的思想。
好了，有了评判树的结构好坏的标准，我们就可以先求最佳的树结构，这个定出来后，最佳的叶子结点的值实际上在上面已经求出来了。
问题是：树的结构近乎无限多，一个一个去测算它们的好坏程度，然后再取最好的显然是不现实的。所以，我们仍然需要采取一点策略，这就是逐步学习出最佳的树结构。这与我们将K棵树的模型分解成一棵一棵树来学习是一个道理，只不过从一棵一棵树变成了一层一层节点而已。

我们以上文提到过的判断一个人是否喜欢计算机游戏为例子。最简单的树结构就是一个节点的树。我们可以算出这棵单节点的树的好坏程度obj*。假设我们现在想按照年龄将这棵单节点树进行分叉，我们需要知道：

1、按照年龄分是否有效，也就是是否减少了obj的值
2、如果可分，那么以哪个年龄值来分。

为了回答上面两个问题，我们可以将这一家五口人按照年龄做个排序。如下图所示：

按照这个图从左至右扫描，我们就可以找出所有的切分点（上图是一种）。对每一个确定的切分点，我们衡量切分好坏的标准如下：

这个Gain实际上单个节点切分后，左、右节点的obj*之和减去切分后的obj*，Gain如果是正的，并且值越大，表示切分后obj越小于单节点的obj，就越值得切分。同时，我们还可以观察到，Gain的左半部分如果小于右侧的γ，则Gain就是负的，表明切分后obj反而变大了。γ在这里实际上是一个临界值，它的值越大，表示我们对切分后obj下降幅度要求越严。这个值也是可以在XGBoost中设定的。
扫描结束后，我们就可以确定是否切分，如果切分，对切分出来的两个节点，递归地调用这个切分过程，我们就能获得一个相对较好的树结构。

注意：XGBoost的切分操作和普通的决策树切分过程是不一样的。普通的决策树在切分的时候并不考虑树的复杂度，而依赖后续的剪枝操作来控制。XGBoost在切分的时候就已经考虑了树的复杂度，就是那个γ参数。所以，它不需要进行单独的剪枝操作。

本文引用：
https://www.jianshu.com/p/7467e616f227
https://www.cnblogs.com/zongfa/p/9324684.html
https://xgboost.readthedocs.io/en/latest/tutorials/model.html