机器学习之svm

概念

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

算法原理

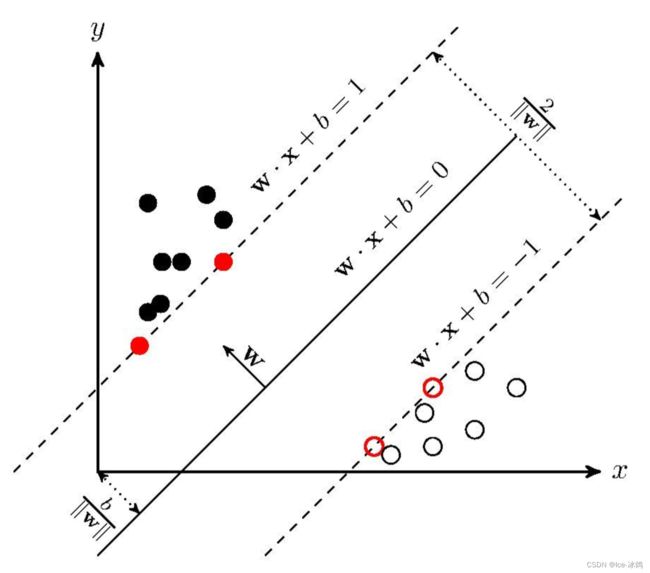
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如上图所示，$w\ast x+b=0$ 即为分离超平面，对于线性可分的数据集来说，这样的超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。

原理推导

为了使间隔$\frac{2}{\Vert W\Vert }$最小化，即使$\frac{1}{2}\Vert W\Vert$最大化，此处保留1/2的目的为方便求导是消去2。但存在约束条件$y_i(W^T{x}_i+b)\le 1$这就是SVM的基本型

问题分析

拉格朗日乘子法

对上述式子使用拉格朗日乘子，得到拉格朗日函数为：$$L(x,b,\alpha )=\frac{1}{2}\Vert w\Vert +\sum _{i=1}^m{\alpha }_i(1-y_i(W^T{x}_i+b))$$
令其对w，b的偏导为0可得
$$W=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$$
$$0=\sum _{i=1}^m{\alpha }_i{y}_i$$
代回拉格朗日函数后即可得到对偶问题：
$$\underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0$$此时只需解出α即可求出w和b从而得到模型

KKT条件

注意到SVM的基本型中有不等式约束，因此上式需要满足KKT条件：
$$\left\{\begin{array}{c}{\alpha }_i\ge 0\\ y_{i}f(x_i)-1\ge 0\\ {\alpha }_i(y_{i}f(x_i)-1)=0\end{array}\right\}$$

代码实现

导入包

import csv
import numpy as np
import matplotlib.pyplot as plt
import copy
from time import sleep
import random
import types

数据处理

def loadDataset(filename):
    with open(filename, 'r') as f:
        lines = csv.reader(f)
        data_set = list(lines)
    if filename != 'titanic.csv':
        for i in range(len(data_set)):
            del(data_set[i][0])
    # 整理数据
    for i in range(len(data_set)):
        del(data_set[i][0])
        del(data_set[i][2])
        data_set[i][4] += data_set[i][5]
        del(data_set[i][5])
        del(data_set[i][5])
        del(data_set[i][6])
        del(data_set[i][-1])

    category = data_set[0]

    del (data_set[0])
    # 转换数据格式
    for data in data_set:
        data[0] = int(data[0])
        data[1] = int(data[1])
        if data[3] != '':
            data[3] = float(data[3])
        else:
            data[3] = None
        data[4] = float(data[4])
        data[5] = float(data[5])
    # 补全缺失值 转换记录方式 分类
    for data in data_set:
        if data[3] is None:
            data[3] = 28
        # male : 1, female : 0
        if data[2] == 'male':
            data[2] = 1
        else:
            data[2] = 0
# 经过测试，如果不将数据进行以下处理，分布会过于密集，处理后，数据的分布变得稀疏了
        # age <25 为0, 25<=age<31为1，age>=31为2
        if data[3] < 25:
            data[3] = 0
        elif data[3] >= 21 and data[3] < 60: # 但是测试得60分界准确率最高？？？！！！
            data[3] = 1
        else:
            data[3] = 2
        # sibsp&parcg以2为界限，小于为0，大于为1
        if data[4] < 2:
            data[4] = 0
        else:
            data[4] = 1
        # fare以64为界限
        if data[-1] < 64:
            data[-1] = 0
        else:
            data[-1] = 1


    return data_set, category

def split_data(data):

    data_set = copy.deepcopy(data)

    data_mat = []
    label_mat = []
    for i in range(len(data_set)):
        if data_set[i][0] == 0:
            data_set[i][0] = -1

        label_mat.append(data_set[i][0])
        del(data_set[i][0])
        data_mat.append(data_set[i])

    print(data_mat)
    print(label_mat)

    return data_mat, label_mat

SVM

def select_j_rand(i ,m):
    # 选取alpha
    j = i
    while j == i:
        j = int(random.uniform(0, m))
    return j
    
def clip_alptha(aj, H, L):
    # 修剪alpha
    if aj > H:
        aj = H
    if L > aj:
        aj = L

    return aj

def smo(data_mat_In, class_label, C, toler, max_iter):
    # 转化为numpy的mat存储
    data_matrix = np.mat(data_mat_In)
    label_mat = np.mat(class_label).transpose()
    # data_matrix = data_mat_In
    # label_mat = class_label
    # 初始化b，统计data_matrix的纬度
    b = 0
    m, n = np.shape(data_matrix)
    # 初始化alpha，设为0
    alphas = np.mat(np.zeros((m, 1)))
    # 初始化迭代次数
    iter_num = 0
    # 最多迭代max_iter次
    while iter_num < max_iter:
        alpha_pairs_changed = 0
        for i in range(m):
            # 计算误差Ei
            fxi = float(np.multiply(alphas, label_mat).T*(data_matrix*data_matrix[i, :].T)) + b
            Ei = fxi - float(label_mat[i])
            # 优化alpha，松弛向量
            if (label_mat[i]*Ei < -toler and alphas[i] < C) or (label_mat[i]*Ei > toler and alphas[i] > 0):
                # 随机选取另一个与alpha_j成对优化的alpha_j
                j = select_j_rand(i, m)
                # 1.计算误差Ej
                fxj = float(np.multiply(alphas, label_mat).T*(data_matrix*data_matrix[j, :].T)) + b
                Ej = fxj - float(label_mat[j])
                # 保存更新前的alpha，deepcopy
                alpha_i_old = copy.deepcopy(alphas[i])
                alpha_j_old = copy.deepcopy(alphas[j])
                # 2.计算上下界L和H
                if label_mat[i] != label_mat[j]:
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L == H:
                    print("L == H")
                    continue
                # 3.计算eta
                eta = 2.0 * data_matrix[i, :]*data_matrix[j, :].T - data_matrix[i, :]*data_matrix[i, :].T - data_matrix[j, :]*data_matrix[j, :].T
                if eta >= 0:
                    print("eta >= 0")
                    continue
                # 4.更新alpha_j
                alphas[j] -= label_mat[j]*(Ei - Ej)/eta
                # 5.修剪alpha_j
                alphas[j] = clip_alptha(alphas[j], H, L)
                if abs(alphas[j] - alphas[i]) < 0.001:
                    print("alpha_j变化太小")
                    continue
                # 6.更新alpha_i
                alphas[i] += label_mat[j]*label_mat[i]*(alpha_j_old - alphas[j])
                # 7.更新b_1和b_2
                b_1 = b - Ei - label_mat[i]*(alphas[i] - alpha_i_old)*data_matrix[i, :]*data_matrix[i, :].T - label_mat[j]*(alphas[j] - alpha_j_old)*data_matrix[i, :]*data_matrix[j, :].T
                b_2 = b - Ej - label_mat[i]*(alphas[i] - alpha_i_old)*data_matrix[i, :]*data_matrix[j, :].T - label_mat[j]*(alphas[j] - alpha_j_old)*data_matrix[j, :] * data_matrix[j, :].T
                # 8.根据b_1和b_2更新b
                if 0 < alphas[i] and C > alphas[i]:
                    b = b_1
                elif 0 < alphas[j] and C > alphas[j]:
                    b = b_2
                else:
                    b = (b_1 + b_2)/2
                # 统计优化次数
                alpha_pairs_changed += 1
                # 打印统计信息
                print("第%d次迭代 样本：%d , alpha优化次数：%d" % (iter_num, i, alpha_pairs_changed))
        # 更新迭代次数
        if alpha_pairs_changed == 0:
            iter_num += 1
        else:
            iter_num = 0
        print("迭代次数：%d" % iter_num)

    return b, alphas


def caluelate_w(data_mat, label_mat, alphas):
    # 计算w
    alphas = np.array(alphas)
    data_mat = np.array(data_mat)
    label_mat = np.array(label_mat)

    # numpy.tile(A, reps):通过重复A给出的次数来构造数组。

    # numpy中reshape函数的三种常见相关用法
    # reshape(1, -1)转化成1行：
    # reshape(2, -1)转换成两行：
    # reshape(-1, 1)转换成1列：
    # reshape(-1, 2)转化成两列

    w = np.dot((np.tile(label_mat.reshape(1, -1).T, (1, 5))*data_mat).T, alphas)
    return w.tolist()

主程序

if __name__ == "__main__":
    test_set, category = loadDataset('titanic_test.csv')
    data_set, category = loadDataset('titanic_train.csv')

    test_mat, test_label = split_data(test_set)
    data_mat, label_mat = split_data(data_set)

    b, alphas = smo(data_mat, list(label_mat), 0.6, 0.001, 40)
    print(b)
    print(alphas)
    w = caluelate_w(data_mat, label_mat, alphas)
    print(w)

    print(test_mat)
    print(test_label)
    result = prediction(test_mat, w, b)

    count = 0
    for i in range(len(result)):
        if result[i] == test_label[i]:
            count += 1

    print(count)

    print(f'the accuracy is {count/len(result)}')

测试结果

可以看出准确率较高为76.5%

总结

• SVM的优势在于解决小样本、非线性和高维的回归和二分类问题。

• 小样本，是指与问题的复杂度相比，SVM要求的样本数相对较少。

• 非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过核函数和松弛变量来实现，这一块才是SVM的精髓。

• 高维，是指样本维数很高，因为SVM 产生的分类器很简洁，用到的样本信息很少，仅仅用到支持向量。

• 由于分类器仅由支持向量决定，SVM还能够有效避免过拟合。