机器学习----回归问题

1.序言

这个系列主要总结一些自己在coursera上的课堂笔记。cousera上的机器学习课程是大名鼎鼎的Andrew NG(吴恩达)老师讲的，讲的深入浅出，真的是良心课程。课程录制在2011年，当时各种DNN还没有那么火，CNN用到图像分类是在2012年，所以课程的内容有点旧，但机器学习的思想仍是很重要的。

2.简介

ML(Mechine Learing)叫做机器学习，我们在网上看到的垃圾邮件的过滤，自动识别标记图片，搜索引擎的排名，以及目前的CV,NLP领域都会用到机器学习算法。机器学习不同的大牛有不同的定义，这里不去引这些例子，咬文嚼字的事情交给大牛们去做，还是希望我们在学习时能够像机器一样，不带任何情绪，扯远了。

目前公认的机器学习算法分为两个大类：监督学习(supervised learning)和无监督学习(unsupervised learning)
监督学习中包括：回归问题(连续型)和聚类问题(离散型)。无监督学习有聚类问题和非聚类问题。这个小结主要研究回归问题中的线性回归。

3.线性回归问题(linear regression)

3.1 单变量线性回归模型

回归问题（拟合问题）就指利用现有的数据，找出一个数学表达式，这个表达式能很好的描述这些数据的变化趋势，我们先研究最简单的单变量的情况，直接用一个图来说明 :

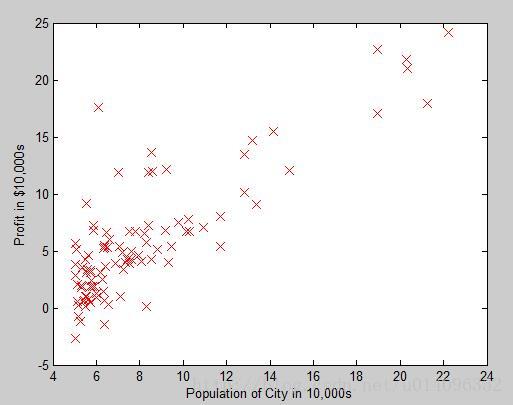
Andrew的课程作业中的例子是用城市的人口来估计某种商品在这个城市销售的利润，从图中我们可以看出，人口与利润是存在着一定的线性关系的，我们现在要做的就是找出这条直线。上边是研究问题的表述，我们用数学模型的方法重新描述一下这个问题。
从长期的观察中，我们发现某种商品利润( y )与人口(x)是存在着一定的线性关系的，我们为了找出这种线性关系收集到一定数量(m 组)的数据，其中的某一组数据我们记为 (x(i),y(i)) ，这些数据被称为 训练集(Training Set)。如果两个变量有线性关系，一定可以用一条直线来表示，所以，我们 假设(hypothesis注意这里的名词，这些数据看上去像是线性关系，所以只能 假设)这条直线为：

hθ(x)=θ0+θ1x

现在的任务就变成了如何选取 θ0,θ1 使得这条直线能更好的描述模型。注意，在这里选不同的 θ0,θ1 会产生不同的直线，如下图：

如何评价到底哪条直线才能更好的表达模型呢？这里我们引入 带价函数(Cost Function)：

J(θ0,θ1)=12m∑i=1m(hθ(x(i))−y(i))2

这个表达式的解释就是：数据集中的每组数据都计算一个差，即通过假设直线预测出的 y^=hθ(x(i)) 的值与真实的 y(i) 值之间的差，因为差有正有负，消除符号的影响我们给差加平方，最后把所有计算出的差取平均就得到一个衡量总体偏差的带价函数，至于为什么要取2，之后的讲解中就会明白。我们的目标就是让这个带价越小越好，因为小的带价意味着预测出的结果与真实结果偏差小，至此为止，单变量线性回归的就完全搞清楚了我们用简单的数学模型来描述一下：

假设：

hθ(x)=θ0+θ1x

求参数：

θ0,θ1

带价函数：

J(θ0,θ1)=12m∑i=1m(hθ(x(i))−y(i))2

目标：

minJ(θ0,θ1)

我们先来研究这个模型的简化，即先以一个参数入手，我们看看这其中的回归思想，简化的模型描述为：

假设：

hθ(x)=θ1x

求参数：

θ1

带价函数：

J(θ1)=12m∑i=1m(hθ(x(i))−y(i))2

目标：

minJ(θ1)

3.1.2一个参数的情况

假设我们的数据集为只有三组数据， (1,1),(2,2),(3,3)

如果我们取 θ1=1 ,这时 hθ(x)=x ,这三组点恰好在这条直线上，所以我们的

J(θ1)=12m∑i=1m(hθ(x(i))−y(i))2=12m(0+0+0)=0

同样的道理，如果取 θ1=0.5 ,这时 hθ(x)=0.5x ，一样可以算出一个 J(θ1) ,这时 J(θ1)≈0.58 ,取 θ1=0 , J(θ1)≈2.3 ,这样，我们就能画出一条Cost function的图像

我们发现带价函数其实是关于 θ1 的一元二次函数，当 θ1=1 时，带价函数达到最小值，且最小值为0，说明模型能够完美拟合数据集！当cost function的最小值不为0时，模型不能完美拟合数据集，只能在误差最小程度上拟合。

3.1.3多个参数的情况

我们接下来看两个参数的情况，从上边一个参数情况，可以看出cost function其实是抛物线，那么两个参数时，cost function张什么样呢？对了，是抛物面！如下图：

还有一种画等高图的方法略过，按照这个规律，3个参数，4个参数，…,n个参数，当然我们的认知范围仅限3维，3个以上的参数是无法想出来它的函数图像的，但是我们根据这以上的两个图是可以找出规律的，就是： 带价函数一定是凸函数，在数学上，一个凸集一定是存在最小值的，严格在证明略过，用在我们这个问题里就是： 带价函数一定有最小值。好了，最小值的存在性已经完美解决，接下来就是如何去找这个最小值了，有高等数学思想的同学一定会想到有两种思路： 解析法和 数值法，前者是用一个表达式表示这个解，后者值用迭代的方法找出这个解的近似。我们先说数值解，这就是我们常说的： 梯度下降法(他的本质是数值微分！)

3.1.4梯度下降法

这里先说梯度下降法的适用范围：某个函数的局部最优解是全局最优解！否则不同的初始位置为找到不同的最小值，梯度下降法最直观的理解就是，假如你站在山上，找到下山最快的那条路径，如果我们有从山顶仍一枚硬币，硬币下山的路径就是梯度下降法。直接给出用梯度下降法求参数的迭代公式：

θj:=θj−α∂∂θjJ(θ0,θ1)(j=0,1)

当有两个参数时，上述公式就变成

θ0:=θ0−α∂∂θ0J(θ0,θ1)θ1:=θ1−α∂∂θ1J(θ0,θ1)

要注意的是，上述两个式子一定要 同时更新！！！！
式中的 α 称作 学习率它反映的是梯度下降法的步长， α 取太大时每一步的步长太大，很可能越过最小值从而找不到最小值， α 太小时收敛的会很慢！我们看一下一个参数的梯度下降法的步骤：

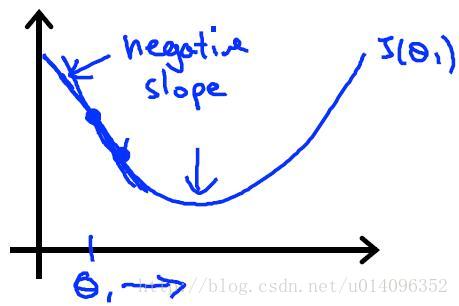
假设从初始的 θ1 =0是，每迭代一次， θ1 都会向着最小值的方向走一步，数学上可以严格证明， 在 α 固定时梯度下降法总可以找到最优解！
我们把梯度下降法运用到线性回归中，即把 J(θ0,θ1) 的表达式代入之前提到的公式，运用多元函数求导规则得到：

θ0:=θ0−α1m∑i=1m(hθ(x(i))−y(i))θ1:=θ1−α1m∑i=1m(hθ(x(i))−y(i))x(i)

写成向量形式就是：

θ:=θ−α1mXT(h(X)−y)

回到我们最开始提到的问题，用梯度下降法找出的直线如下：

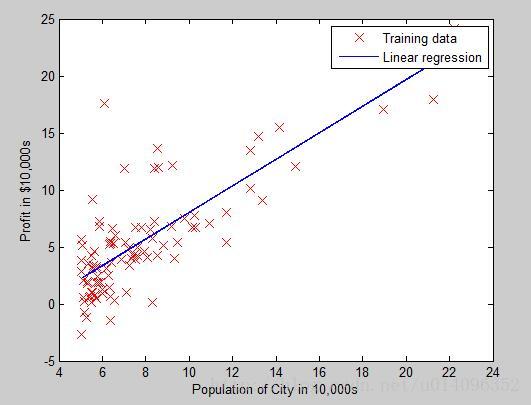
4多变量线性回归

4.1.1多个参数与梯度下降法

按照单变量线性回归的模型，直接做维度的扩展

假设：

hθ(x)=∑i=0mθixi=θTx

其中 x0=1
求参数：

θ0,θ1,...,θn

带价函数：

J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2

目标：

minJ(θ0,θ1,...,θn)

按照上边形式化的推导，我们很容易得出多变量回归的梯度下降法

θj:=θj−α∂∂θjJ(θ0,θ1,...,θn)(j=0,1,...,n)

代入 J(θ0,θ1,...,θn) 的表达式得

θ1:=θ1−α1m∑i=1m(hθ(x(i))−y(i))x(i)(j=0,1,...,n)

到这里，看起来一切那么顺其自然，等等，多个变量时会出现新的问题，由于不同的变量有不同的取值范围，如果两个变量的取值范围相差的太大则梯度下降法会很慢很慢，我们要做的就是把变量 归一化处理。数学上用来做归一化的方法有很多，这里推荐一种，如下：

x(i)=x(i)−μs

其中 μ 是数据集中变量 x(i) 的均值， s 是标准差，不要忘记在做预测时仍需要做标准化处理！

4.1.2梯度下降法中的学习率

为了考察梯度下降法中带价函数的变化，我们通常画J(θ)关于迭代次数的函数，如下图：

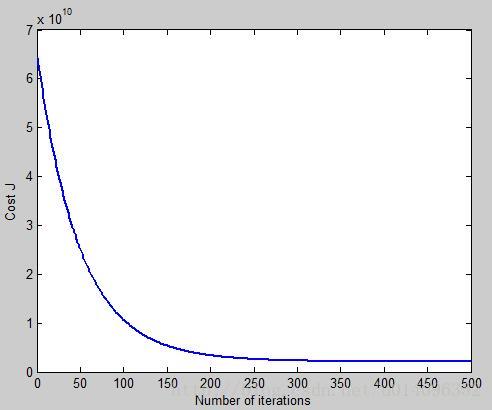
如果函数下降的太慢，说明学习率 α 选的太小，如果函数不是下降而是其他的形状，说明学习率 α 选得太大，NG推荐的一个学习率选择的方法是分别试0.001,0.003,0.01,0.03,0.1,0.3…

4.1.3多项式回归

与多变量的线性回归类似，多项式回归的模型如下：

假设：

hθ(x)=∑i=0mθixii=θTx

其中 x0=1
求参数：

θ0,θ1,...,θn

带价函数：

J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2

目标：

minJ(θ0,θ1,...,θn)

在真正做回归时只需要做简单的变量替换 x=xi ，同样的思路，这用变换可以用到对数函数，指数函数的回归！这里不展开讲，真正做的的时候很容易把对数函数通过两边取指数变成线性函数，或者把指数函数两边取对数变成线性函数。

5解析法

我们之前提到，求 J(θ) 的最小值也可以用解析法！有一定多元微积分基础的同学就会知道，对每个变量求偏导，再让它们等于0就可以找到最值！数学表达式为：

J(θ0,θ1,...,θn)=12m∑i=1m(hθ(x(i))−y(i))2∂∂θ1J(θ0,θ1,...,θn)=∂∂θ2J(θ0,θ1,...,θn)=...=∂∂θnJ(θ0,θ1,...,θn)=0

解得：

θ=(XTX)−1XTy

用解析法找到的解一定是精确解，但是计算机在求大型矩阵的逆时会很费时，所以在变量的个数大于10000时推荐用梯度下降，小于10000时可以考虑解析法，有些童鞋会问，如果矩阵不可逆时怎么办？这时求逆时用广义逆(可以翻看矩阵论)。
好了，至此所有关于回归问题的方法已经介绍完，近期将不定期更新分类问题。