Eigen——线性代数运算的C++模板库

    前几天，帮着师兄改写程序，需要将Mathematica编写的程序用C语言翻译出来并运行出结果。这几天下来也算对Eigen有了初步的了解。写一下，希望对大家有所帮助。

在最初选择C++矩阵运算库是，主要参考了如下两篇文，

http://blog.csdn.net/chenbang110/article/details/12304123

http://blog.csdn.net/houston11235/article/details/8501135

目前比较主流的矩阵运行库有Armadillo,Eigen ,OpenCV，在选择C++矩阵库时，主要看大家实际情况，这里就对Eigen做初步介绍。深入学习请参考 http://eigen.tuxfamily.org/dox/，也可以下载它的离线下载包学习 http://eigen.tuxfamily.org/dox/index.html。

Eigen——线性代数运算的C++模板库，面向矩阵，向量，数值运算以及相关的 运算。

使用Eigen准备工作

Eigen官网上下载Eigen源码库函数包 http://eigen.tuxfamily.org/index.php?title=Main_Page，将它解压到一个不含中文的目录下。

下面就是安装Eigen，我是基于Visual Studio 2010的Windows开发，运行VS2010,创建一个基于Win32控制台应用程序的空项目，在解决方案资源管理器中右击源文件，添加C++文件，粘贴如下代码：

#include

#include

using Eigen::MatrixXd;

int main()

{

MatrixXd m(2,2);

m(0,0) = 3;

m(1,0) = 2.5;

m(0,1) = -1;

m(1,1) = m(1,0) + m(0,1);

std::cout << m << std::endl;

}

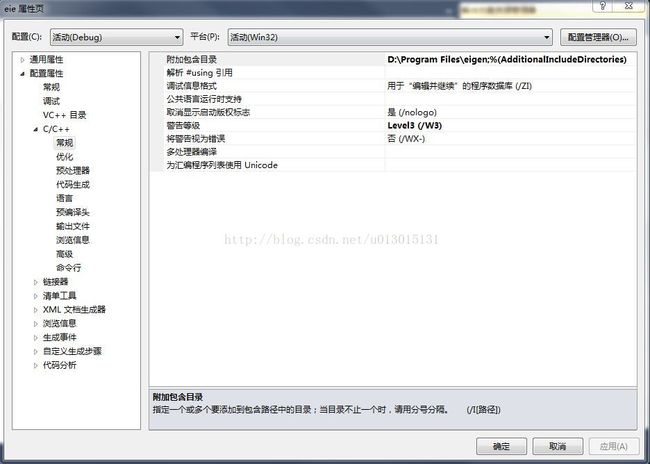
右击项目->属性->C/C++->常规->附加包含目录，添加解压后的Eigen库函数包。

输出3     -1

    2.5   1.5   输出成功！

Eigen矩阵运算的简单介绍

 Eigen provides two kinds of dense objects: mathematical matrices andvectors which are both represented by the template class Matrix, and general 1D and 2D arrays represented by the template class Array:

这两种类型的变量主要区别：1、Matrix类型变量加减法若行列数不相等，不能做加减。Array类型的变量是可以加减一个常数，作用是各个元素分别加减该常数；2、Matrix与Array类型变量做乘法也会不同，Matrix是矩阵相乘，Array对应元素相乘；

Matrix 与Array可以相互转换，方法 .array()和.matrix()。如下：

#include #include using namespaceEigen; using namespacestd; int main() { MatrixXf m(2,2); MatrixXf n(2,2); MatrixXf result(2,2); m << 1,2, 3,4; n << 5,6, 7,8; result = m * n; cout << "-- Matrix m*n: --" << endl << result << endl << endl; result = m.array() * n.array(); cout << "-- Array m*n: --" << endl << result << endl << endl; result = m.cwiseProduct(n); cout << "-- With cwiseProduct: --" << endl << result << endl << endl; result = m.array() + 4; cout << "-- Array m + 4: --" << endl << result << endl << endl; }

-- Matrix m*n: -- 19 22 43 50 -- Array m*n: -- 5 12 21 32 -- With cwiseProduct: -- 5 12 21 32 -- Array m + 4: -- 5 6 7 8

如下是Eigen关于Matrix与Array类型的运算操作（详细参见官网）：

Basic matrix manipulation

	1D objects	2D objects	Notes
Constructors	Vector4d v4; Vector2f v1(x, y); Array3i v2(x, y, z); Vector4d v3(x, y, z, w); VectorXf v5; // empty object ArrayXf v6(size);	Matrix4f m1; MatrixXf m5; // empty object MatrixXf m6(nb_rows, nb_columns);	By default, the coefficients  are left uninitialized
Comma initializer	Vector3f v1; v1 << x, y, z; ArrayXf v2(4); v2 << 1, 2, 3, 4;	Matrix3f m1; m1 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
Comma initializer (bis)	int rows=5, cols=5; MatrixXf m(rows,cols); m << ( Matrix3f() << 1, 2, 3, 4, 5, 6, 7, 8, 9).finished(), MatrixXf::Zero(3,cols-3), MatrixXf::Zero(rows-3,3), MatrixXf::Identity(rows-3,cols-3); cout << m;		output: 1 2 3 0 0 4 5 6 0 0 7 8 9 0 0 0 0 0 1 0 0 0 0 0 1
Runtime info	vector.size(); vector.innerStride(); vector.data();	matrix.rows(); matrix.cols(); matrix.innerSize(); matrix.outerSize(); matrix.innerStride(); matrix.outerStride(); matrix.data();	Inner/Outer* are storage order dependent
Compile-time info	ObjectType::Scalar ObjectType::RowsAtCompileTime ObjectType::RealScalar ObjectType::ColsAtCompileTime ObjectType::Index ObjectType::SizeAtCompileTime
Resizing	vector.resize(size); vector.resizeLike(other_vector); vector.conservativeResize(size);	matrix.resize(nb_rows, nb_cols); matrix.resize(Eigen::NoChange, nb_cols); matrix.resize(nb_rows, Eigen::NoChange); matrix.resizeLike(other_matrix); matrix.conservativeResize(nb_rows, nb_cols);	no-op if the new sizes match, otherwise data are lost resizing with data preservation
Coeff access with  range checking	vector(i) vector.x() vector[i] vector.y() vector.z() vector.w()	matrix(i,j)	Range checking is disabled if  NDEBUG or EIGEN_NO_DEBUG is defined
Coeff access without range checking	vector.coeff(i) vector.coeffRef(i)	matrix.coeff(i,j) matrix.coeffRef(i,j)
Assignment/copy	object = expression; object_of_float = expression_of_double.cast< float>();		the destination is automatically resized (if possible)

    Array operators:

Arithmetic operators	array1 * array2 array1 / array2 array1 *= array2 array1 /= array2 array1 + scalar array1 - scalar array1 += scalar array1 -= scalar
Comparisons	array1 < array2 array1 > array2 array1 < scalar array1 > scalar array1 <= array2 array1 >= array2 array1 <= scalar array1 >= scalar array1 == array2 array1 != array2 array1 == scalar array1 != scalar
Trigo, power, and  misc functions  and the STL variants	array1.min(array2) array1.max(array2) array1.abs2() array1.abs() abs(array1) array1.sqrt() sqrt(array1) array1.log() log(array1) array1.exp() exp(array1) array1.pow(exponent) pow(array1,exponent) array1.square() array1.cube() array1.inverse() array1.sin() sin(array1) array1.cos() cos(array1) array1.tan() tan(array1) array1.asin() asin(array1) array1.acos() acos(array1)

   Arithmetic Operators

add  subtract	mat3 = mat1 + mat2; mat3 += mat1; mat3 = mat1 - mat2; mat3 -= mat1;
scalar product	mat3 = mat1 * s1; mat3 *= s1; mat3 = s1 * mat1; mat3 = mat1 / s1; mat3 /= s1;
matrix/vector  products *	col2 = mat1 * col1; row2 = row1 * mat1; row1 *= mat1; mat3 = mat1 * mat2; mat3 *= mat1;
transposition  adjoint *	mat1 = mat2.transpose(); mat1.transposeInPlace(); mat1 = mat2.adjoint(); mat1.adjointInPlace();
dot product  inner product *	scalar = vec1.dot(vec2); scalar = col1.adjoint() * col2; scalar = (col1.adjoint() * col2).value();
outer product *	mat = col1 * col2.transpose();
norm  normalization *	scalar = vec1.norm(); scalar = vec1.squaredNorm() vec2 = vec1.normalized(); vec1.normalize(); // inplace
cross product *	#include vec3 = vec1.cross(vec2);

使用Eigen矩阵库运算结果与Mathematica运算结果丝毫不差！