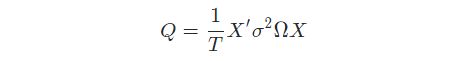python 回归 statsmodels_FamaMacbeth 回归和NeweyWest调整

1. 综述

Fama Macbeth是一种通过回归方法做因子检验，并且可以剔除残差截面上自相关性的回归方法，同时为了剔除因子时序上的自相关性，可以通过Newey West调整对回归的协方差进行调整。

2. 原理

2.1 系数估计

Fama Macbeth回归分为两步，第一步是横截面回归 ，在截面上用股票收益率对各因子暴露做回归，得到各因子的收益率；第二部是对系数的时间序列取平均得到作为参数的估计值，并进行t检验，t检验用到的标准误经过Newey West调整，总结如下

2.2 标准误估计

• 简单估计

其中，分子上为回归系列的标准差，可以直接计算，也可以进行Newey West调整消除异方差和序列自相关。

• Newey West 调整

 Newey West的原理主要参考了石川大佬的文章[2][3]，简单说明，考虑一个线性模型

当残差不存在异方差和自相关性时，残差协方差阵为单位阵的倍数，回归系数的协方差估计是一致估计量，当残差存在异方差或自相关性时，协方差阵估计有问题，可以通过Newey West调整解决，具体来说是估计上式中的

Newey West调整即对Q进行估计，最终给出的估计量具有一致性，表达式如下，用S表示

上式中，括号中第一项为仅有异方差时的调整，后面一项为针对自相关的调整，其中，e为样本残差，L为计算自相关性影响的最大滞后阶数，w_l是滞后期l的系数，从公式来看，随着滞后期数的增加，影响减小。将S带入系数协方差阵的估计可以得到协方差的Newey West估计量

其中，L常用的取法有很多种，python的famamacbeth函数的取法包括

以上是对于OLS的Newey West调整，对于Fama Macbeth回归，是对已经回归出来的一堆beta系数序列的方差进行调整，跟回归有一定差别，可以做一个转换：用回归出来的所有beta做因变量，1做自变量，做一个回归，这样回归出来的系数是所有beta的均值，残差也捕捉了beta中的异方差性和自相关性，对这个回归方程做newey west即可，这个在石川大佬的文章中有更细致的说明。

3. Python实现

Python的linearmodels中自带FamaMacBeth函数，本文一方面调用这一函数，另一方面自己写，用两种方法实现Fama Macbeth回归，确保结果的准确性。

数据使用2010-2018年全A股的市值、动量、PB、roe因子进行测试。

3.1 数据载入

from linearmodels import FamaMacBeth
import numpy as np
import pandas as pd

import datetime

import statsmodels.api as sm
import statsmodels.formula.api as sml

def getICSeries(factors,ret,method):
    

    icall = pd.DataFrame()
    fall = pd.merge(factors,ret,left_on = ['tradedate','stockcode'],right_on = ['tradedate','stockcode'])
    icall = fall.groupby('tradedate').apply(lambda x:x.corr(method = method)['ret']).reset_index()
    icall = icall.drop(['ret'],axis = 1).set_index('tradedate')

    return icall


def ifst(x):
    if pd.isnull(x.entry_dt):
        return 0
    elif (x.tradedate < x.entry_dt) |(x.tradedate > x.remove_dt):
        return 0
    else:
        return 1


def ols_coef(x,y):
    x = x.astype('float64')
    y = y.astype('float64')

    return sm.OLS(y,sm.add_constant(x),missing = 'drop').fit().params



def ols_coef1(x,formula):
    return sml.ols(formula, data=x).fit(missing = 'drop').params
price = pd.read_csv('price.csv',index_col = 0)
pb = pd.read_csv('pb.csv',index_col = 0)
roe = pd.read_csv('roe.csv',index_col = 0)
mkt = pd.read_csv('mkt.csv',index_col = 0)
ST = pd.read_excel('ST.xlsx')

'''
收益率计算
'''

price['tradedate'] = price.tradedate.apply(getdate)
ret_m = getRet(price,freq ='m',if_shift = True)
mom1 = getRet(price,freq ='m',if_shift = False)
mom1 = mom1.rename(columns = {'ret':'mom1'})

fall = pd.merge(pb,roe,left_on = ['tradedate','stockcode'],right_on = ['tradedate','stockcode'])
fall = pd.merge(fall,mkt,left_on = ['tradedate','stockcode'],right_on = ['tradedate','stockcode'])
fall['tradedate'] = fall.tradedate.apply(getdate)
fall = pd.merge(fall,mom1,left_on = ['tradedate','stockcode'],right_on = ['tradedate','stockcode'])
del fall['rptdate']




fall = pd.merge(fall,ST,left_on = 'stockcode',right_on = 'stockcode',how = 'left')
fall['if_st'] = fall.apply(ifst,axis = 1)
fall = fall.loc[fall.if_st == 0].reset_index(drop = True)
fall = fall.drop(['if_st','entry_dt','remove_dt'],axis = 1)


alldata = pd.merge(fall,ret_m,left_on = ['tradedate','stockcode'],right_on = ['tradedate','stockcode'])
alldata['mktcap'] = np.log(alldata.mktcap)

3.2 计算因子IC

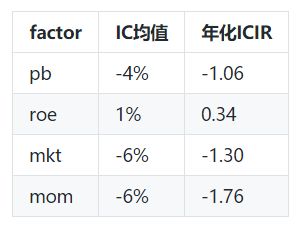
alldata中包含所有的因子和收益率数据，并且已经剔除了ST，用alldata做测试。首先用alldata计算因子的IC，ICIR结果如下

ics = getICSeries(fall,ret_m,'spearman')
icir = ics.mean()/ics.std()*np.sqrt(12)
ics.cumsum().plot()

3.3 Fama macbeth回归

接下来用这四个因子做FamaMacbeth回归，首先用python自带的函数FamaMacbeth

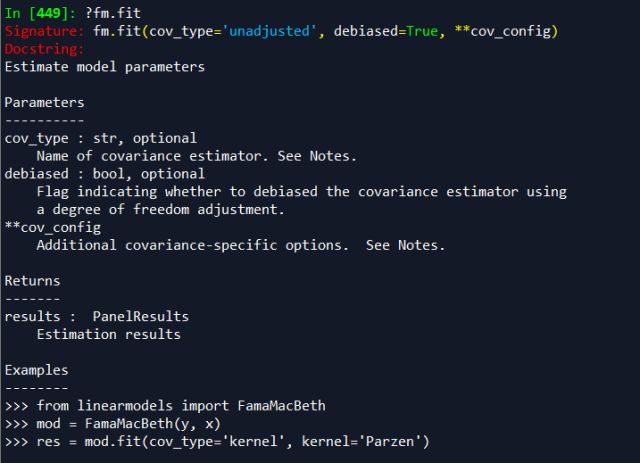
这个函数用法和statsmodels中的OLS基本一致，输入因变量(dependent)，自变量(exog)和样本权重(weights)，需要注意的是因变量、自变量都是面板数据，或者用MultiIndex的dataframe，日期在前，个体编码在后。生成FamaMacbeth对象后用fit方法进行系数估计,fit的输入参数较多

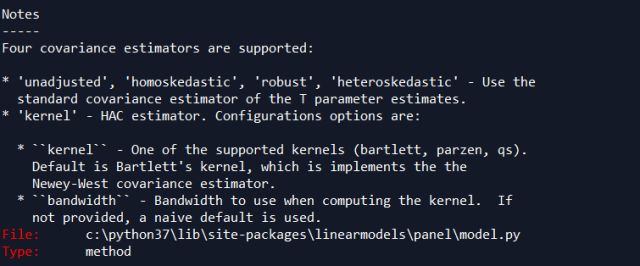
• cov_type表示是否对方差进行调整，'unadjusted'表示不调整，默认为不调整。'kernel'表示调整，即用Newey West方法进行调整

• debiased：是否对协方差进行自由度调整，即分母用n还是n-1

• bandwitdh：窗宽，即上文NW调整中的L，如果不设置会通过算法自动生成最优的，也可以根据上面L的公式手动输入。

关于这两个函数的细致说明可以参考[1]，这里首先给出不进行调整的回归结果

fmdata = alldata.set_index(['stockcode','tradedate'])
fm = FamaMacBeth(dependent = fmdata['ret'],
                 exog = sm.add_constant(fmdata[['pb','mktcap','mom1','roe_ttm']]))
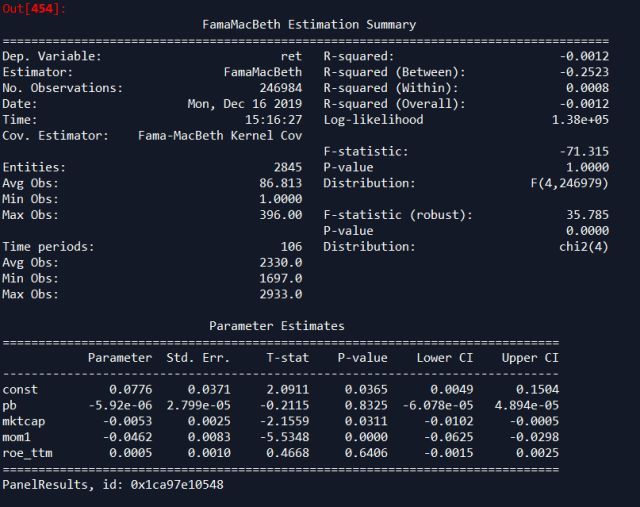
res_fm = fm.fit(debiased=False)
res_fm

手动回归并与上述结果相对比

res = alldata.dropna().groupby('tradedate').apply(ols_coef1,'ret ~ 1 + pb + mktcap + mom1 + roe_ttm')
res.mean()

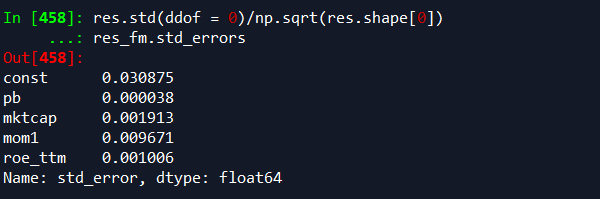
res.std(ddof = 0)/np.sqrt(res.shape[0])

• 回归系数

• 回归标准误

接下来看Newey West调整后的结果，这里根据上面的公式计算最优的L

T = res.shape[0]
L = int(np.ceil(4 * (T / 100) ** (2 / 9)))

取bandwidth = 5，NW调整后的回归结果如下

res_fm = fm.fit(cov_type= 'kernel',debiased = False,bandwidth = 5)
res_fm

手动回归，用beta序列对1进行回归，对结果做NW调整，这里回归用statsmodels中的OLS函数构造辅助函数ols_nw_se完成，最大滞后阶数也设置为5，返回标准误

def ols_nw_se(y):
    return sm.OLS(y.values,np.ones(len(y))).fit(missing = 'drop',cov_type = 'HAC',cov_kwds={'maxlags':5}).bse

res.apply(ols_nw_se,axis = 0)

最后对回归结果做简单分析，从FM结果来看，市值和动量通过了显著性检验，方向与IC的方向一致，表明因子对股票收益率有一定的解释力，pb、roe未能通过检验，表明这两个因子中的信息有跟其他两个重叠了，没有信息增益。但是要说明本文建模整个过程都比较粗糙，只是为实现FM回归，结论不具有一般性。

获取数据源码，后台回复"famamacbeth"

参考文献

[1]https://bashtage.github.io/linearmodels/panel/models.html#linearmodels.panel.model.FamaMacBeth 

[2] https://zhuanlan.zhihu.com/p/40984029 

[3] https://zhuanlan.zhihu.com/p/54913149

[4] Fama E F, MacBeth J D. Risk, return, and equilibrium: Empirical tests[J]. Journal of political economy, 1973, 81(3): 607-636.