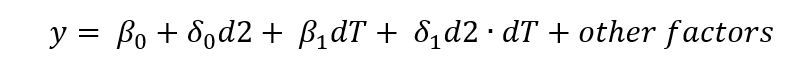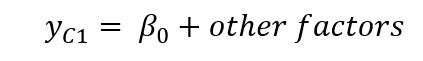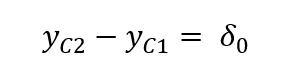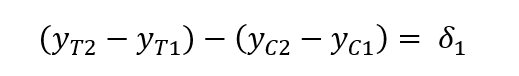r语言 面板数据回归_R语言——伍德里奇计量经济导论案例实践 第十三章 横截面与面板数据(一)...
哈喽,停更了大概有三周的计量笔记又要重新开始啦!虽然美国的疫情没有停歇的迹象,可是依旧阻挡不了大学开学的热情。从8月3号开始上课到现在,也经历了很多事情,每天都是抱着死猪不怕开水烫的心情,暗地里安慰自己已经群体免疫。除了疫情外,最让人头疼的就是开学后的各种作业啦,计量的各种证明题着实易让人崩溃。幸好,每次翻开伍德里奇的教材都有种亲切感,所以这本书的计量笔记还能继续更新。从第十三章开始,这本书就进入了第三部分,涉及的内容是一些较为高级的计量模型。使用伍德里奇这本教材授课,一般不会涉及第三部分的章节,除非计量课程分两个学期进行授课。第十三章的前半部分讲述了独立混合横截面数据 (independently pooled cross section 我的中文翻译很可能是错的 

 ) 的分析方法,后半部分讲述了面板数据 (panel data) 的分析方法。因为内容太多,所以我的笔记也分成两篇,今天这篇先讲independently pooled cross section有关的内容。简言之,独立混合横截面数据就是在时间轴上选取不同的时间节点对总体数据进行抽样。比如为了研究某地区某项政策对女性职场收入的影响,我们在政策实施之前对该地区的女性进行抽样调查获得横截面数据,在政策实施两年后,再进行一次随机抽样调查获得横截面数据,因为第二次也是随机抽样,所以第一次受访的调查对象有可能会再次接受采访,也可能没有接受到采访。而面板数据在不同的时间节点并没有都进行随机抽样,只有在第一个时间节点进行了随机抽样,而后就固定跟踪观察第一次随机抽样的观察对象,记录相应数据,有点类似于时间序列。比如同样是研究女性职场收入,面板数据在第一次进行随机抽样后,两年后是对第一次的受访女性进行回访,采集到新的薪酬数据。如果你还没太明白,那就是我中文解释的太烂~在这里还是推荐阅读原版教材,英语解释概念确实较为清晰。
) 的分析方法,后半部分讲述了面板数据 (panel data) 的分析方法。因为内容太多,所以我的笔记也分成两篇,今天这篇先讲independently pooled cross section有关的内容。简言之,独立混合横截面数据就是在时间轴上选取不同的时间节点对总体数据进行抽样。比如为了研究某地区某项政策对女性职场收入的影响,我们在政策实施之前对该地区的女性进行抽样调查获得横截面数据,在政策实施两年后,再进行一次随机抽样调查获得横截面数据,因为第二次也是随机抽样,所以第一次受访的调查对象有可能会再次接受采访,也可能没有接受到采访。而面板数据在不同的时间节点并没有都进行随机抽样,只有在第一个时间节点进行了随机抽样,而后就固定跟踪观察第一次随机抽样的观察对象,记录相应数据,有点类似于时间序列。比如同样是研究女性职场收入,面板数据在第一次进行随机抽样后,两年后是对第一次的受访女性进行回访,采集到新的薪酬数据。如果你还没太明白,那就是我中文解释的太烂~在这里还是推荐阅读原版教材,英语解释概念确实较为清晰。
一、Independently Pooled Cross Section使用混合独立横截面数据的一大动力就是可以获得容量更大的样本,如果我们假设自变量对因变量的效应在不同的时间点是不变的,比如每多接受一年教育对薪酬的效应在1990年是增加0.98美元,在2000年依然是增加0.98美元,那么使用混合独立横截面数据就不会带来特别大的问题,并且因为样本容量大了,我们的估计值就可以更精确 (还记得第四章渐近性的内容嘛)。不过因变量在不同的时间节点的期望值分布可能会有所不同,所以一般我们会使用year dummy来允许我们的线性回归方程在不同的时间节点有不同的截距,同时又保证了自变量的局部效应是不变的。书上的例子13.1: Women's Fertility over Time就是典型的混合独立横截面,数据 fertil1包括了从1972年到1984年偶数年份的对美国女性生育率的随机抽样调查,年份在这里被设置为了dummy variable,当我们控制了其他可能影响生育率的变量之后,如果year dummy的系数还是显著的,即表明不同时间点的生育率有着大不同,而这些不同并不是因为被控制的变量造成的。 下面是该例子的R语言代码: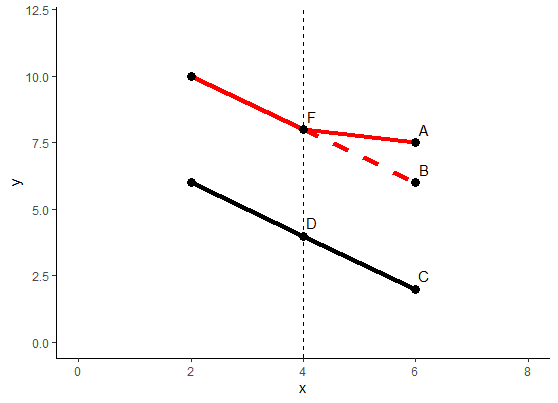 如果用计量回归方程来表示,即为:
这里的d2和dT均为dummy variable,d2 = 1即表示在实验之后,dT = 1即表示属于实验组。当dT = 1, d2 = 0时:
当dT = 1, d2 = 1时:
通过差分可获得实验组试验前后的自变量的变化:
当dT = 0, d2 = 0时:
当dT = 0, d2 = 1时:
通过差分可获得对照组试验前后的自变量的变化:
通过双重差分获得treatment effect:
我们在差分的过程中把可能影响因变量的因素都消除掉了,最后剩下的系数即为施加处理后的效应。我们以书中的eg 13.3: Effect of a Garbage Incinerator's Location on Housing Prices为例,所使用的数据为 kielmc,这个案例探究了在住宅区附近修建垃圾焚烧厂对房价的影响。直觉上看,在住宅周边修建垃圾焚烧厂肯定会使房价下跌,但是影响房价的因素有很多,比如房子已经建成的时间、房子的大小等等,我们希望通过双重差分法来消除其他因素对房价的影响,确定垃圾焚烧厂与房价之间的因果关系。我们在回归中使用了两个dummy,y81 = 1时表示时间点在1981年即修建垃圾焚烧厂之后,nearinc = 1表示房子距离垃圾焚烧厂较近。
如果用计量回归方程来表示,即为:
这里的d2和dT均为dummy variable,d2 = 1即表示在实验之后,dT = 1即表示属于实验组。当dT = 1, d2 = 0时:
当dT = 1, d2 = 1时:
通过差分可获得实验组试验前后的自变量的变化:
当dT = 0, d2 = 0时:
当dT = 0, d2 = 1时:
通过差分可获得对照组试验前后的自变量的变化:
通过双重差分获得treatment effect:
我们在差分的过程中把可能影响因变量的因素都消除掉了,最后剩下的系数即为施加处理后的效应。我们以书中的eg 13.3: Effect of a Garbage Incinerator's Location on Housing Prices为例,所使用的数据为 kielmc,这个案例探究了在住宅区附近修建垃圾焚烧厂对房价的影响。直觉上看,在住宅周边修建垃圾焚烧厂肯定会使房价下跌,但是影响房价的因素有很多,比如房子已经建成的时间、房子的大小等等,我们希望通过双重差分法来消除其他因素对房价的影响,确定垃圾焚烧厂与房价之间的因果关系。我们在回归中使用了两个dummy,y81 = 1时表示时间点在1981年即修建垃圾焚烧厂之后,nearinc = 1表示房子距离垃圾焚烧厂较近。


 ) 的分析方法,后半部分讲述了面板数据 (panel data) 的分析方法。因为内容太多,所以我的笔记也分成两篇,今天这篇先讲independently pooled cross section有关的内容。简言之,独立混合横截面数据就是在时间轴上选取不同的时间节点对总体数据进行抽样。比如为了研究某地区某项政策对女性职场收入的影响,我们在政策实施之前对该地区的女性进行抽样调查获得横截面数据,在政策实施两年后,再进行一次随机抽样调查获得横截面数据,因为第二次也是随机抽样,所以第一次受访的调查对象有可能会再次接受采访,也可能没有接受到采访。而面板数据在不同的时间节点并没有都进行随机抽样,只有在第一个时间节点进行了随机抽样,而后就固定跟踪观察第一次随机抽样的观察对象,记录相应数据,有点类似于时间序列。比如同样是研究女性职场收入,面板数据在第一次进行随机抽样后,两年后是对第一次的受访女性进行回访,采集到新的薪酬数据。如果你还没太明白,那就是我中文解释的太烂~在这里还是推荐阅读原版教材,英语解释概念确实较为清晰。
) 的分析方法,后半部分讲述了面板数据 (panel data) 的分析方法。因为内容太多,所以我的笔记也分成两篇,今天这篇先讲independently pooled cross section有关的内容。简言之,独立混合横截面数据就是在时间轴上选取不同的时间节点对总体数据进行抽样。比如为了研究某地区某项政策对女性职场收入的影响,我们在政策实施之前对该地区的女性进行抽样调查获得横截面数据,在政策实施两年后,再进行一次随机抽样调查获得横截面数据,因为第二次也是随机抽样,所以第一次受访的调查对象有可能会再次接受采访,也可能没有接受到采访。而面板数据在不同的时间节点并没有都进行随机抽样,只有在第一个时间节点进行了随机抽样,而后就固定跟踪观察第一次随机抽样的观察对象,记录相应数据,有点类似于时间序列。比如同样是研究女性职场收入,面板数据在第一次进行随机抽样后,两年后是对第一次的受访女性进行回访,采集到新的薪酬数据。如果你还没太明白,那就是我中文解释的太烂~在这里还是推荐阅读原版教材,英语解释概念确实较为清晰。
一、Independently Pooled Cross Section使用混合独立横截面数据的一大动力就是可以获得容量更大的样本,如果我们假设自变量对因变量的效应在不同的时间点是不变的,比如每多接受一年教育对薪酬的效应在1990年是增加0.98美元,在2000年依然是增加0.98美元,那么使用混合独立横截面数据就不会带来特别大的问题,并且因为样本容量大了,我们的估计值就可以更精确 (还记得第四章渐近性的内容嘛)。不过因变量在不同的时间节点的期望值分布可能会有所不同,所以一般我们会使用year dummy来允许我们的线性回归方程在不同的时间节点有不同的截距,同时又保证了自变量的局部效应是不变的。书上的例子13.1: Women's Fertility over Time就是典型的混合独立横截面,数据 fertil1包括了从1972年到1984年偶数年份的对美国女性生育率的随机抽样调查,年份在这里被设置为了dummy variable,当我们控制了其他可能影响生育率的变量之后,如果year dummy的系数还是显著的,即表明不同时间点的生育率有着大不同,而这些不同并不是因为被控制的变量造成的。 下面是该例子的R语言代码:
### 导入数据处理包library(tidyverse)### 导入数据library(wooldridge)### 导入相关检验命令符包library(lmtest)library(car)### 导入数据输出包library(stargazer)### 添加year dummy进行回归lm_fertility 2) + black + east + northcen + west + farm + othrural + town + smcity + y74 + y76 + y78 + y80 + y82 + y84, data = fertil1)summary(lm_fertility)### 在R语言中我们一般把dummy当作factor进行处理### 我们可以把数据里的年份变量设置为dummy然后对year这一个变量进行回归### 效果和上面的单独设置year dummy是一样的### 创建新的表格 将year设置为factorfer % mutate(year = factor(year)) ### 对year进行回归lm_fer 2) + black + east + northcen + west + farm + othrural + town + smcity + year, data = fer)summary(lm_fer)
当我们控制住其他可能影响生育率的变量后,根据结果我们可以发现,和1972年相比,生育率在1982年和1984年急剧下降,根据t statistic和p-value我们也可发现结果是显著的。在生育率这个例子中,我们假设了自变量在不同时间点对因变量的局部效应是恒定的,比如在我们的回归结果中,自变量 educ受教育年限的系数值约为-0.128,即当其他变量不变时,100位多接受一年教育的女性平均会少生大概12个孩子,这个效果在不同的年份都是一样的。但我们都知道,这是非常不符合实际情况的,比如随着教育的普及,多接受一年教育对薪酬的局部效应在1950年和在1990年肯定是不同的。在之前的第七章我们已经提到过,我们可以添加year dummy与自变量的交互项来允许改变不同时间节点的自变量的系数值。课本中的eg 13.2: Changes in the Return to Education and the Gender Wage Gap研究了1978年和1985年这两个不同年份的关于薪酬的横截面数据。我们在回归中加入了year dummy和year dummy与自变量 educ以及 gender的交互项,如果year dummy和交互项的系数都是显著的,也即表明薪酬在1978年和1985年这两个不同时间节点有着不同的分布。使用数据 cps78_85,下面为R语言代码:### 对year进行回归lm_cps 2) + union + female + female:y85, data = cps78_85)summary(lm_cps) 如果用计量回归方程来表示,即为:
这里的d2和dT均为dummy variable,d2 = 1即表示在实验之后,dT = 1即表示属于实验组。当dT = 1, d2 = 0时:
当dT = 1, d2 = 1时:
通过差分可获得实验组试验前后的自变量的变化:
当dT = 0, d2 = 0时:
当dT = 0, d2 = 1时:
通过差分可获得对照组试验前后的自变量的变化:
通过双重差分获得treatment effect:
我们在差分的过程中把可能影响因变量的因素都消除掉了,最后剩下的系数即为施加处理后的效应。我们以书中的eg 13.3: Effect of a Garbage Incinerator's Location on Housing Prices为例,所使用的数据为 kielmc,这个案例探究了在住宅区附近修建垃圾焚烧厂对房价的影响。直觉上看,在住宅周边修建垃圾焚烧厂肯定会使房价下跌,但是影响房价的因素有很多,比如房子已经建成的时间、房子的大小等等,我们希望通过双重差分法来消除其他因素对房价的影响,确定垃圾焚烧厂与房价之间的因果关系。我们在回归中使用了两个dummy,y81 = 1时表示时间点在1981年即修建垃圾焚烧厂之后,nearinc = 1表示房子距离垃圾焚烧厂较近。
如果用计量回归方程来表示,即为:
这里的d2和dT均为dummy variable,d2 = 1即表示在实验之后,dT = 1即表示属于实验组。当dT = 1, d2 = 0时:
当dT = 1, d2 = 1时:
通过差分可获得实验组试验前后的自变量的变化:
当dT = 0, d2 = 0时:
当dT = 0, d2 = 1时:
通过差分可获得对照组试验前后的自变量的变化:
通过双重差分获得treatment effect:
我们在差分的过程中把可能影响因变量的因素都消除掉了,最后剩下的系数即为施加处理后的效应。我们以书中的eg 13.3: Effect of a Garbage Incinerator's Location on Housing Prices为例,所使用的数据为 kielmc,这个案例探究了在住宅区附近修建垃圾焚烧厂对房价的影响。直觉上看,在住宅周边修建垃圾焚烧厂肯定会使房价下跌,但是影响房价的因素有很多,比如房子已经建成的时间、房子的大小等等,我们希望通过双重差分法来消除其他因素对房价的影响,确定垃圾焚烧厂与房价之间的因果关系。我们在回归中使用了两个dummy,y81 = 1时表示时间点在1981年即修建垃圾焚烧厂之后,nearinc = 1表示房子距离垃圾焚烧厂较近。
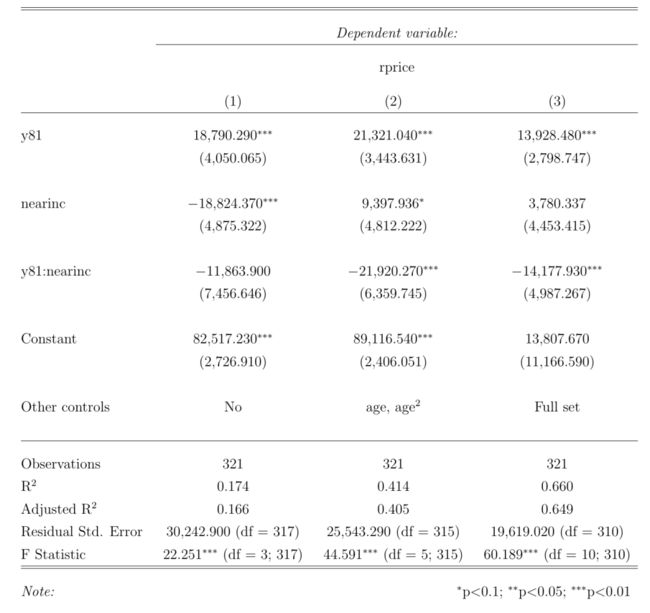
### 未添加控制变量 仅有year dummy和lm_price1 ### 添加age变量 即房子已经建成多久lm_price2 2), data = kielmc)### 继续添加新的控制变量 包括大小、房间数量等lm_price3 2) + intst + land + area + rooms + baths, data = kielmc)### 输出表格 在LaTex中显示### 表格中只显示了dummy的系数值和截距### 表格中最后一行Other controls是我在LaTex代码中手动添加的stargazer(lm_price1, lm_price2, lm_price3, omit = c("age", "I(age^2)", "intst", "land", "area", "rooms", "baths"))