08.1. 序列模型

8.1. 序列模型

电影评分看法的改变，一些原因：

• 锚定效应
• 享乐适应
• 季节性
• 场外因素

序列数据的应用场景：

• 股价
• 语音、文本数据
• 地震，余震
• 人类之间的互动等

8.1.1. 统计工具

处理序列数据需要统计工具和新的深度神经网络架构。

8.1.1.1. 自回归模型

输入数据的数量这个数字将会随着我们遇到的数据量的增加而增加， 因此需要一个近似方法来使这个计算变得容易处理。

• 自回归模型（autoregressive models）：
  满足长度为L的时间跨度，对下一个跨度进行预测
• 隐变量自回归模型（latent autoregressive models）
  保留一些对过去观测的总结， 并且同时更新预测和总结
  
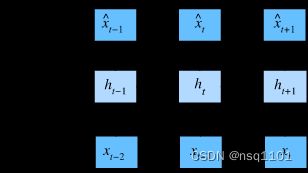
  隐变量自回归模型

如何生成训练数据？
一个经典方法是使用历史观测来预测下一个未来观测。

8.1.1.2. 马尔可夫模型

一阶马尔可夫模型（first-order Markov model）：
当前预测只和前一个时刻的数据相关

8.1.1.3. 因果关系

未来的事件不能影响过去

8.1.2. 训练

在了解了上述统计工具后，让我们在实践中尝试一下！
首先，我们生成一些数据：使用正弦函数和一些可加性噪声来生成序列数据：

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

T = 1000  # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

接下来，我们将这个序列转换为模型的“特征－标签”（feature-label）对. 在这里，我们仅使用前600个“特征－标签”对进行训练。

tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):
   features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))

batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                           batch_size, is_train=True)

# 使用一个相当简单的架构训练模型： 一个拥有两个全连接层的多层感知机，ReLU激活函数和平方损失。
# 初始化网络权重的函数
def init_weights(m):
   if type(m) == nn.Linear:
       nn.init.xavier_uniform_(m.weight)

# 一个简单的多层感知机
def get_net():
   net = nn.Sequential(nn.Linear(4, 10),
                       nn.ReLU(),
                       nn.Linear(10, 1))
   net.apply(init_weights)
   return net

# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

# train
def train(net, train_iter, loss, epochs, lr):
   trainer = torch.optim.Adam(net.parameters(), lr)
   for epoch in range(epochs):
       for X, y in train_iter:
           trainer.zero_grad()
           l = loss(net(X), y)
           l.sum().backward()
           trainer.step()
       print(f'epoch {epoch + 1}, '
             f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')

net = get_net()
train(net, train_iter, loss, 5, 0.01)

# result
epoch 1, loss: 0.092109
epoch 2, loss: 0.061592
epoch 3, loss: 0.057409
epoch 4, loss: 0.055409
epoch 5, loss: 0.054001

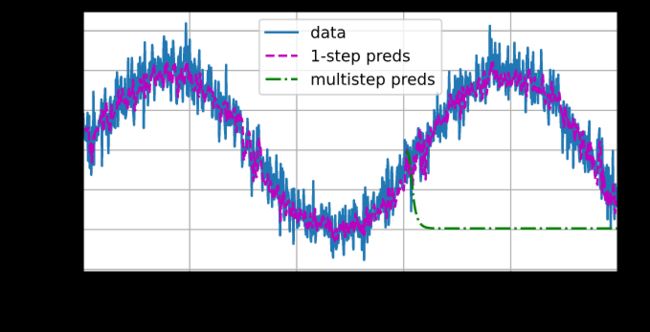
8.1.3. 预测

• 单步预测（one-step-ahead prediction）

onestep_preds = net(features)
d2l.plot([time, time[tau:]],
        [x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
        'x', legend=['data', '1-step preds'], xlim=[1, 1000],
        figsize=(6, 3))

• 多步预测

multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
   multistep_preds[i] = net(
       multistep_preds[i - tau:i].reshape((1, -1)))

d2l.plot([time, time[tau:], time[n_train + tau:]],
        [x.detach().numpy(), onestep_preds.detach().numpy(),
         multistep_preds[n_train + tau:].detach().numpy()], 'time',
        'x', legend=['data', '1-step preds', 'multistep preds'],
        xlim=[1, 1000], figsize=(6, 3))

通过对整个序列预测的计算， 让我们更仔细地看一下步预测的困难。

max_steps = 64

features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i（i=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):
   features[:, i] = net(features[:, i - tau:i]).reshape(-1)

steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
        [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
        legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
        figsize=(6, 3))

以上例子清楚地说明了当我们试图预测更远的未来时，预测的质量是如何变化的。
虽然“步预测”看起来仍然不错，但超过这个跨度的任何预测几乎都是无用的。

8.1.4. 小结

• 内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测）在实践的难度上差别很大。因此，对于你所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。

• 序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。

• 对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。

• 对于直到时间步的观测序列，其在时间步的预测输出是“步预测”。随着我们对预测时间值的增加，会造成误差的快速累积和预测质量的极速下降。