【专题】最短路算法(2.8k字,非常详细)
图论算法之最短路算法
前言
常见的最短路算法有这些:Floyd、Dijkstra、Bellman-Ford 和 SPFA。其中,SPFA 已经死了,因为它很容易被 hack(洛谷出的测试数据生成器 CYaRon 还有专门的卡 SPFA 函数),且时间复杂度与 Bellman-Ford 几乎没有区别,所以在此不再介绍。
这些算法有哪些区别
有这么多最短路的算法,那他们究竟有什么区别呢?评判这些算法,我们有如下指标:
- 单源 or 全源
- 是否能处理负权边
- 是否能发现负权回路
- 时间复杂度
其中,单源的意思是:从一个点到其他点;全源的意思是:从任意点到任意点。其他的指标都很好理解,就不再赘述。
我将这几个指标汇总成一个表,来更加清晰地发现他们的区别:
| 单源 / 全源 | 负权边 | 负权回路 | 时间复杂度 | |
|---|---|---|---|---|
| F l o y d Floyd Floyd | 全源 | 是 | 否 | O ( N 3 ) O(N^3) O(N3) |
| D i j k s t r a Dijkstra Dijkstra | 单源 | 否 | 否 | O ( N 2 ) O(N^2) O(N2) |
| B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford | 单源 | 是 | 是 | O ( N E ) O(NE) O(NE) |
其中, N N N 代表结点个数, E E E 代表边的个数。
三个算法各有优缺点,在实战中使用最多的是 D i j k s t r a Dijkstra Dijkstra。
下面开始讲解这些算法。
Floyd
这个算法是最简单的最短路径算法。可以计算任意两条边之间的最短路径。
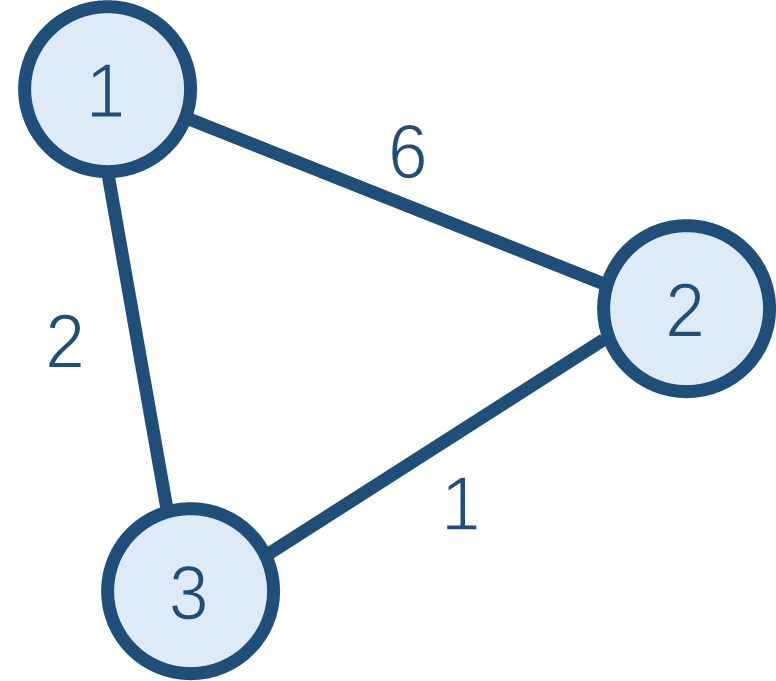
该算法的思想很简单,类似于一个区间 DP。如果点 i i i 到点 k k k 的权值加上点 k k k 到点 j j j 的权值之和小于原先点 i i i 到点 j j j 的权值,那么更新它。例如:
像这个图,原本点 1 1 1 到点 2 2 2 的权值为 6 6 6,现在发现点 1 1 1 到点 3 3 3 的权值加上点 3 3 3 到点 2 2 2 的权值之和( 3 3 3)小于它,所以更新最小值。
PS: dis[u][v] 表示从 u u u 到 v v v 最短路径长度,w[u][v] 表示连接 u , v u, v u,v 的边的权值。
/********** 初始化 **********/
dis[u][v] = w[u][v]; // 如果 u, v 有边相连
dis[u][v] = INF; // 如果 u, v 没有边相连
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (dis[i][j] > dis[i][k] + dis[k][j])
dis[i][j] = dis[i][k] + dis[k][j];
值得注意的是,虽然第一层循环也可以放在 i , j i, j i,j 后面或者 i , j i, j i,j 之间,但是这会导致效率降低,甚至比 O ( N 3 ) O(N^3) O(N3) 还要低,所以枚举中间点的这层循环必须放在最外层。
示例代码:
#include
#include
const int N = 1e3 + 9, INF = 0x3F3F3F3F;
int n, m, a, b, f[N][N];
int main() {
memset(f, INF, sizeof f);
for (int i = 1; i <= n; i++)
f[i][i] = 0;
scanf("%d%d", &n, &m);
for (int i = 1, u, v, w; i <= m; i++) {
scanf("%d%d%d", &u, &v, &w);
f[u][v] = w;
}
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (f[i][j] > f[i][k] + f[k][j])
f[i][j] = f[i][k] + f[k][j];
scanf("%d%d", &a, &b);
if (f[a][b] != INF) printf("%d", f[a][b]);
else puts("-1");
return 0;
}
Dijkstra
这个算法是最常用的最短路径算法。速度也是三个算法中最快的。
该算法用的是贪心的思路,思想是蓝白点。什么是蓝点、白点呢?
白点是已经确定最短路径的点,而蓝点就是未确定最短路径的点。想要求出两点之间的最短路,就是要将一个点作为起点,另一个点变成白点。
本节中,dis[i] 代表从指定起点开始,到点 i i i 的最短路。
贪心的思路是:每次选最小的 dis[i],将 i i i 变为白点,并更新与 i i i 相邻的所有蓝点到起点的最短路 dis[j]。重复这项操作即可。可以看出,这个算法会认为**在同一条路径上,经过的边越多,走的距离越远。**这也是为什么 D i j k s t r a Dijkstra Dijkstra 不能处理负权边的情况。
为了更好的理解,我会通过图示来解释。
为了看的更清晰,我将白点统一画成红点。
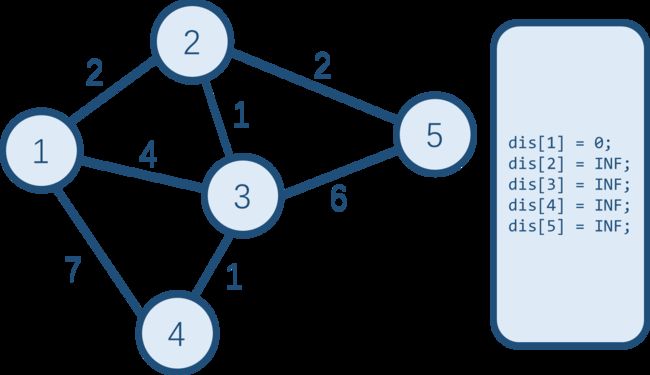
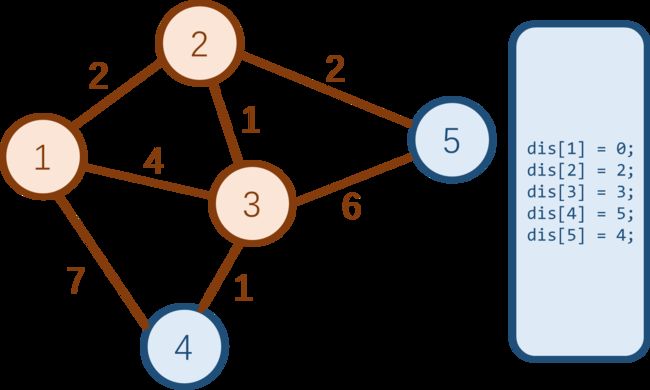
这是初始的图。我们要计算从起点 1 1 1 开始,到各个点的最短路。开始时,起点到起点的最短路为 0 0 0。
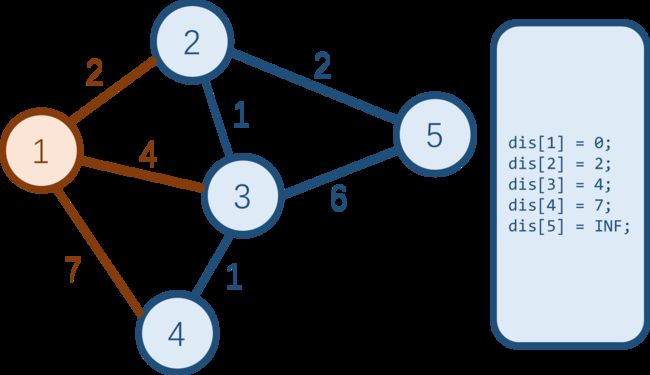
所有蓝点中,dis 值最小的是 1 1 1 号点,把它变为白点后,更新与之相邻的三个蓝点到起点的最短路 dis[2], dis[3], dis[4]。
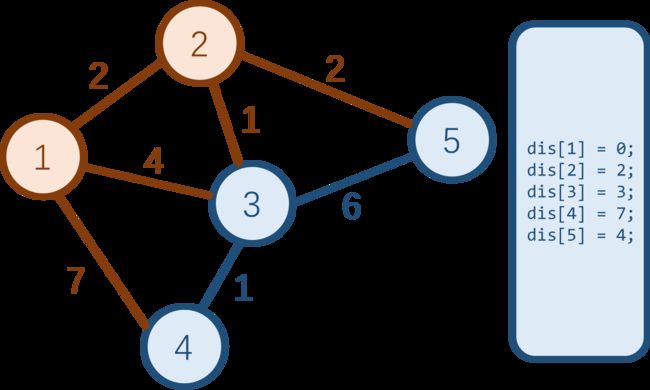
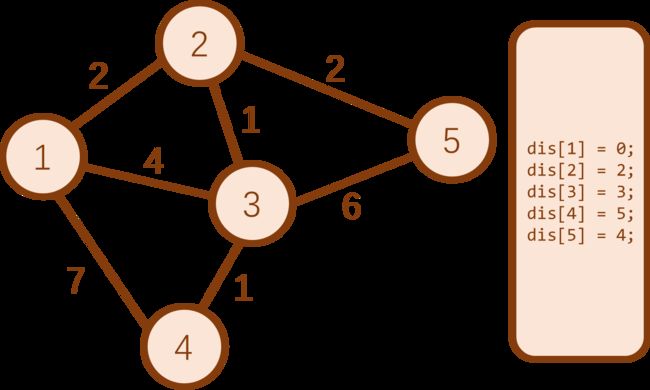
现在,点 2 2 2 是所有蓝点中 dis 值最小的蓝点。所以将其变为白点,并更新与之相邻的两个蓝点的最短路。
现在,点 3 3 3 是所有蓝点中 dis 值最小的蓝点。所以将其变为白点,并更新与之相邻的两个蓝点的最短路。
最后,依次将点 5 5 5、点 4 4 4 变为白点。至此, D i j k s t r a Dijkstra Dijkstra 算法过程结束。
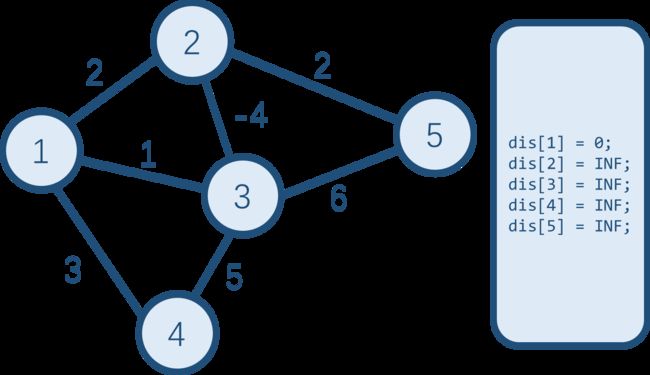
下面举一个负权边的例子,以证明该算法无法处理负权边。
第一步同上,不再说了。
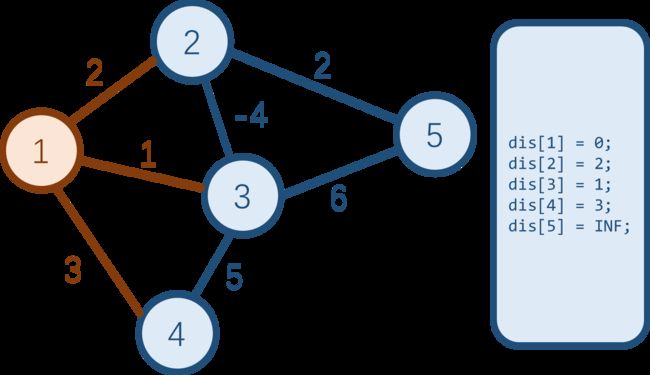
这时候,dis 值最小的蓝点是点 3 3 3。按照 D i j k s t r a Dijkstra Dijkstra 的思路,下一步会把点 3 3 3 设为不再改动的白点。可是,真正的到点 3 3 3 的最短路是 1 → 2 → 3 = − 2 1\rightarrow 2\rightarrow 3 = -2 1→2→3=−2。可以看出, D i j k s t r a Dijkstra Dijkstra 确实不能处理负边权的情况。
代码(Luogu 4779 【模板】单源最短路径(标准版))
#include
#include
const int N = 1e5 + 9, M = 2e5 + 9;
const int INF = 0x3F;
int n, m, s, hd[N], dis[N];
bool isWhiteDot[N];
struct Edge {
int to, nx, wt;
} eg[M];
void addE(int u, int v, int w, int c) {
eg[c] = {v, hd[u], w}, hd[u] = c;
}
void dijkstra() {
memset(dis, 0x3F, sizeof dis);
dis[s] = 0;
for (int i = 1; i < n; i++) {
int u = 0, mn = INF;
for (int j = 1; j <= n; j++)
if (isWhiteDot[j]==false and dis[j] dis[u] + eg[j].wt)
dis[v] = dis[u] + eg[j].wt;
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 1, u, v, w; i <= m; i++) {
scanf("%d%d%d", &u, &v, &w);
addE(u, v, w, i);
}
dijkstra();
for (int i = 1; i <= n; i++)
printf("%d ", dis[i]);
return 0;
}
这个代码可以得 0 0 0 分( T L E TLE TLE),所以我们再来讨论一下优化。
可以发现, D i j k s t r a Dijkstra Dijkstra 代码中的第二层循环的第一个循环的作用就是找最小值。我们有专门的数据结构来处理——堆。堆,即优先级队列,最大的功能就是可以维护一个数列中的最大值或者最小值。所以,我们可以用堆优化 D i j k s t r a Dijkstra Dijkstra。
堆优化后的 D i j k s t r a Dijkstra Dijkstra 板子:
#include
#include
const int N = 1e5 + 9, M = 2e5 + 9;
const int INF = 0x3F;
int n, m, s, hd[N], dis[N];
bool isWhiteDot[N];
struct Edge {
int to, nx, wt;
} eg[M];
void addE(int u, int v, int w, int c) {
eg[c] = {v, hd[u], w}, hd[u] = c;
}
void dijkstra() {
memset(dis, 0x3F, sizeof dis);
dis[s] = 0;
for (int i = 1; i < n; i++) {
int u = 0, mn = INF;
for (int j = 1; j <= n; j++)
if (isWhiteDot[j]==false and dis[j] dis[u] + eg[j].wt)
dis[v] = dis[u] + eg[j].wt;
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 1, u, v, w; i <= m; i++) {
scanf("%d%d%d", &u, &v, &w);
addE(u, v, w, i);
}
dijkstra();
for (int i = 1; i <= n; i++)
printf("%d ", dis[i]);
return 0;
}
Bellman-Ford
与 D i j k s t r a Dijkstra Dijkstra 相同,这个算法也是采用了蓝白点的思想,也是一种单源最短路的算法。但不同的是:
-
它的思路是动态规划
-
它可以处理负边权
-
它可以发现负权回路
B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford 算法的思路很简单。一开始,认为起点是白点,然后枚举所有的边,一定会有一些边连接着蓝点和白点。所以,每次拿现有的白点去更新所有邻接的蓝点,每次循环至少有一个点会从蓝点变成白点。
但 B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford 的蓝白点与 D i j k s t r a Dijkstra Dijkstra 的蓝白点不太一样。 B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford 是用已更新过的点去更新未更新过的点。已更新过的点被称为白点。不同于 D i j k s t r a Dijkstra Dijkstra, B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford 的白点可能还会被更新。
状态定义: f k , i f_{k,i} fk,i 代表从起点出发,最多经过不构成负权回路 k k k 条边后到达点 i i i 的最短路径长度
状态转移:显然, f k , i f_{k,i} fk,i 的值是由 f k − 1 , j ( j ∈ [ 0 , i − 1 ] ) f_{k-1,j}(j\in [0,i-1]) fk−1,j(j∈[0,i−1]) 的值更新而来的。即将 f k − 1 , j ( j ∈ [ 0 , i − 1 ] ) f_{k-1,j}(j\in [0,i-1]) fk−1,j(j∈[0,i−1]) 的终点作为中转点,将这个点连一条边指向 i i i,取两者最小值,即为所要求的最短路径长度。
状态转移方程: f k , u = m i n ( f k − 1 , u , m i n { f k − 1 , j + g j , u } ) f_{k,u} = min(f_{k-1,u},min\{f_{k-1,j}+g_{j,u}\}) fk,u=min(fk−1,u,min{fk−1,j+gj,u})。其中, g j , u g_{j,u} gj,u 表示点 i i i 到点 j j j 的距离。
状态初始化:为了方便书写,我们规定,点 0 0 0 为起点。则根据状态定义, f k , 0 f_{k,0} fk,0 代表从起点出发,最多经过 k k k 条边到达点 0 0 0 的最短路径长度。显然,从起点到起点的最短路径长度一定是 0 0 0,所以只需要把 f k , 0 f_{k,0} fk,0 初始化成 0 0 0,其余初始化成无穷大即可。
那么它是怎么判断负权回路的呢?
如果 B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford 两层循环处理完毕后,发现还存在某条边,使得 f u + w u , v < f v f_u + w_{u,v} < f_v fu+wu,v<fv,就说明一定存在负权回路。
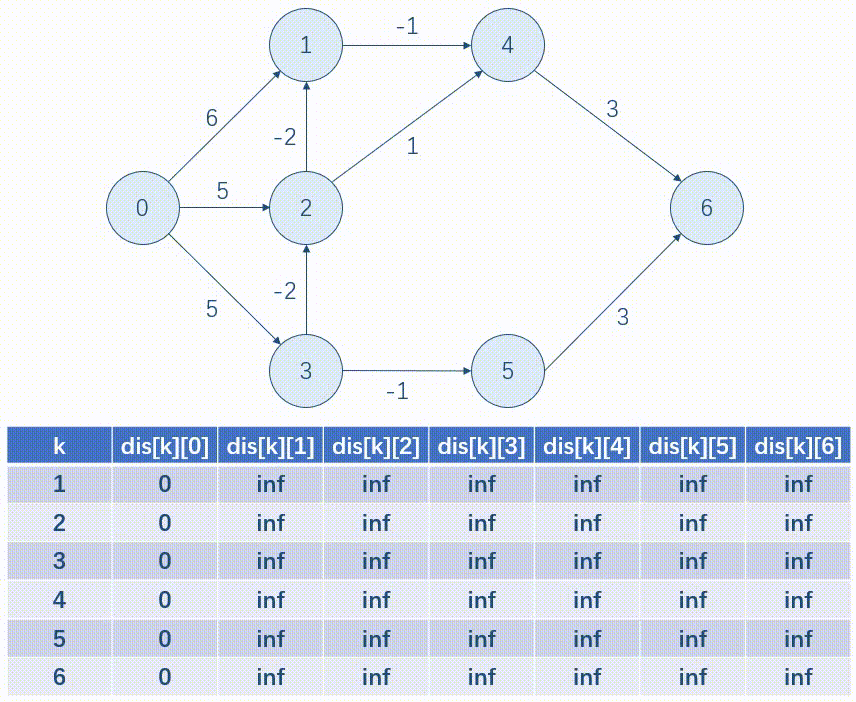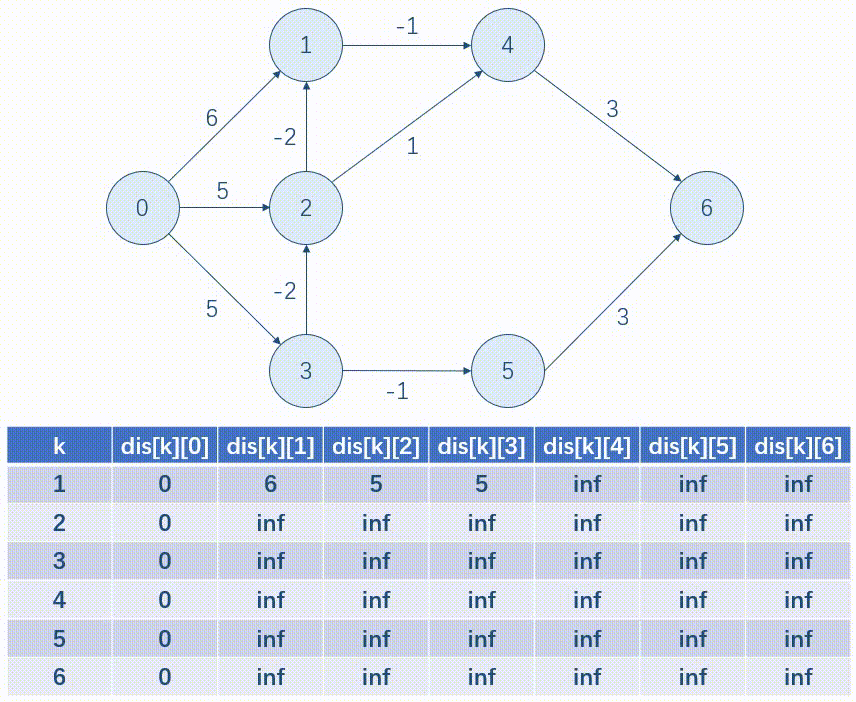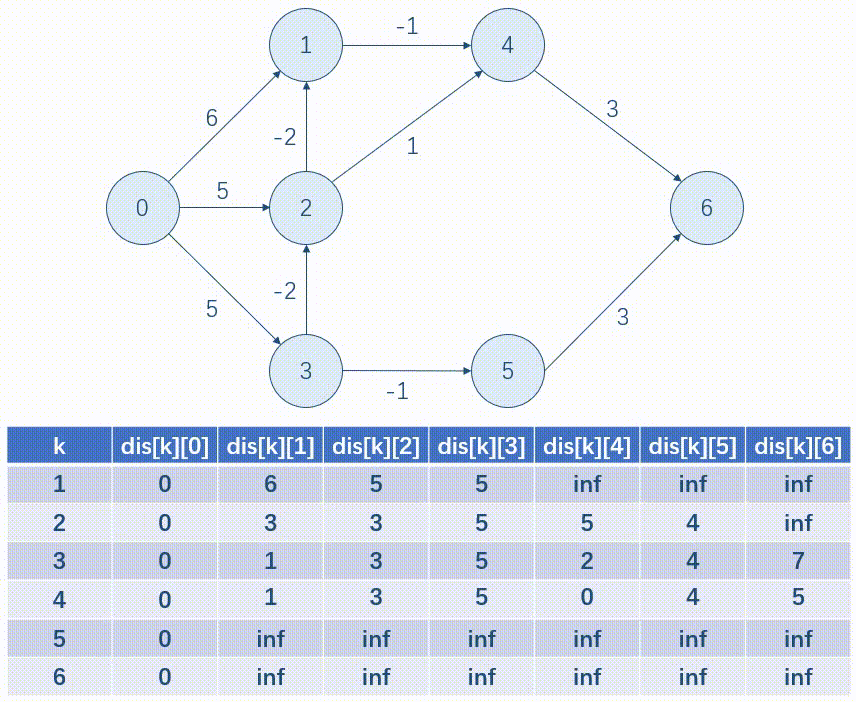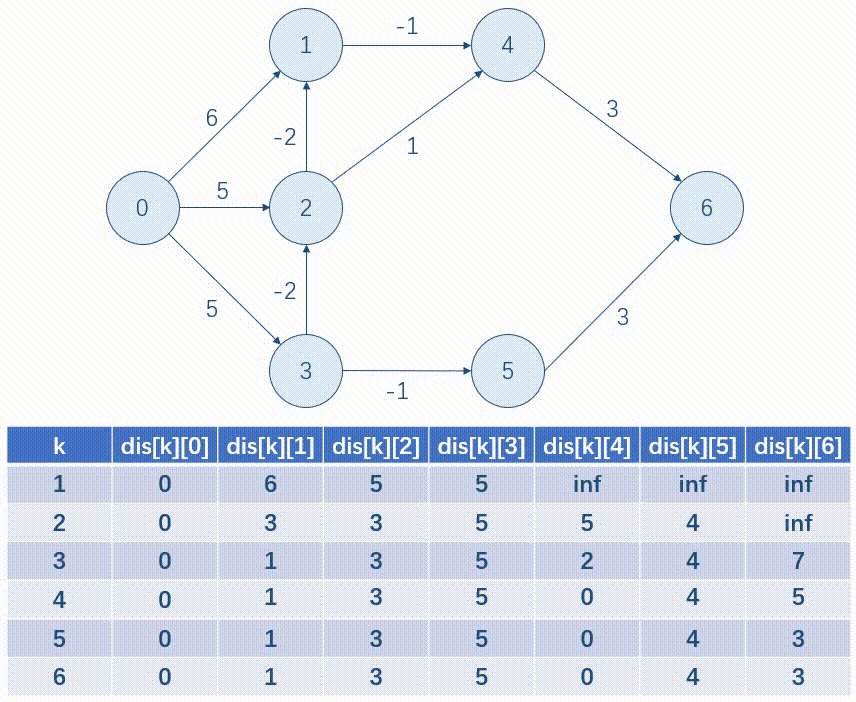
以下面这张图为例,我们用表格的形式模拟一遍 B e l l m a n - F o r d Bellman\text{-}Ford Bellman-Ford。
优化:写完后我们发现,每一次只是按行更新一遍 dis 数组,所以我们可以使用滚动数组的方式来存,这样就可以省去一维。
最终代码(题目链接:AcWing 853. 有边数限制的最短路)
#include
#include
const int N = 509, M = 1e4 + 9, INF = 0x3F3F3F3F;
int n, m, k, dis[N], backup[N];
struct Edge {
int fr, to, wt;
} eg[M];
int bellman_ford() {
memset(dis, 0x3F, sizeof dis);
dis[1] = 0;
for (int i = 1; i <= k; i++) {
memcpy(backup, dis, sizeof dis);
for (int j = 1; j <= m; j++) {
int u = eg[j].fr, v = eg[j].to, w = eg[j].wt;
dis[v] = std::min(dis[v], backup[u] + w);
}
}
if (dis[n] > INF / 2) return -114514; // 这里不要写 return -1,会被卡
return dis[n];
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1, u, v, w; i <= m; i++) {
scanf("%d%d%d", &u, &v, &w);
eg[i] = {u, v, w};
}
int res = bellman_ford();
if (res == -114514) puts("impossible");
else printf("%d", res);
return 0;
}
后记
这篇博客从七月末开始写,到现在九月初才写完。再加上文章篇幅比较长,难免会犯一些错误。如果大家发现了文章的错误,或者认为笔者还有哪里没有介绍清楚,请在 勘误区 中不吝指出,谢谢!
upt(2022/09/04 22:20): 更新了部分无法显示的 LaTeX \LaTeX LATEX。