GMM高斯混合模型及EM算法(matlab和python实现)

【完整代码】

因文章原因，我将GMM实现的matlab和python完整代码放到了我的GitHub了，可以下载验证：
　　GMM实现的matlab和python完整代码

https://github.com/taw19960426/GMM-matlab-python

一、GMM高斯混合模型(matlab)

１.GMM综述

Gaussian Mixture Model ，就是假设数据服从 Mixture Gaussian Distribution ，换句话说，数据可以看作是从数个 Gaussian Distribution 中生成出来的。实际上，我们在 K-means 和 K-medoids 两篇文章中用到的那个例子就是由三个 Gaussian 分布从随机选取出来的。实际上，从中心极限定理可以看出，Gaussian 分布（也叫做正态 (Normal) 分布）这个假设其实是比较合理的，除此之外，Gaussian 分布在计算上也有一些很好的性质，所以，虽然我们可以用不同的分布来随意地构造 XX Mixture Model ，但是还是 GMM 最为流行。另外，Mixture Model 本身其实也是可以变得任意复杂的，通过增加 Model 的个数，我们可以任意地逼近任何连续的概率密分布。

每个 GMM 由 个 Gaussian 分布组成，每个 Gaussian 称为一个“Component”，这些 Component 线性加成在一起就组成了 GMM 的概率密度函数：
$$P(x)=\sum _{k=1}^K{W}_{k}g\left(x|{\mu }_k,\sum _k\right)$$
其中W是权重，X是样本，包含平均值以及协方差$$\left({\mu }_k,{\Sigma }_k\right)$$
根据上面的式子，如果我们要从 GMM 的分布中随机地取一个点的话，实际上可以分为两步：首先随机地在这 个 Component 之中选一个，每个 Component 被选中的概率实际上就是它的系数 ，选中了 Component 之后，再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布，转化为了已知的问题。

2. 案列的引入

在校园里随机抽取2000个学生，其中有男有女，已知男生，女生的身高都服从高斯分布，这两个高斯分布的均值和方差我们都不知道，另外由于某种原因，我们也不知道2000个学生里男生和女生的个数，现在我们要求出两个分布的均值和方差，还有男女比例。

2.1数据准备

我们需要产生两个高斯分布序列，分别代表男女生的身高。需要注意的是，我们在产生序列的时候必须要在知道男女生各占多少的情况下进行随机生成。

%绘制男女生身高的GMM
clc
clear all
%男女生共取2000人，女生平均身高163，男声平均身高180
male=180+sqrt(10)*randn(1,1000);
%产生均值为180，方差为10的一个1*1000的随机数
female=163+sqrt(10)*randn(1,1000);
h=[female male];

对于混合前和混合后的数据如下图所示：

2.2初始化参数

%Step 1.首先根据经验来分别对男女生的均值、方差和权值进行初始化
mu1_first=170;sigmal_first=10;w1_first=0.7;%男生的
mu2_first=160;sigma2_first=10;w2_first=0.3;%以我们学校理工院校为例

2.3计算每个身高的响应R

%Step 2. 
%计算男的身高在男分布中的响应R1i
%计算女的身高在男分布中的响应R2i
h=[female male];%混合
N=2000;
R1i=zeros(1,N);
R2i=zeros(1,N);
for i=1:N
    p1=w1_first*pdf('norm',h(i),mu1_first,sigmal_first);
    p2=w2_first*pdf('norm',h(i),mu2_first,sigma2_first);
    %p1,p2权重*男女生的后验概率
   R1i(i)=p1/(p1+p2);
   R2i(i)=p2/(p1+p2);
end

2.4更新男女分布的期望

以男生为例

%Step 3.
%更新男、女生身高分布的期望mu
s1=0;
s2=0;
for i=1:N
    s1=s1+R1i(i)*h(i);
    s2=s2+R2i(i)*h(i);
end
s11=sum(R1i);
s22=sum(R2i);
mu1_last=s1/s11;
mu2_last=s2/s22;

2.5更新男女分布的标准差

%Step 4.
%更新男、女生身高分布的标准差sigma(一维）
t1=0;
t2=0;
for i=1:N
    t1=t1+R1i(i)*(h(i)-mu1_last)^2;
    t2=t2+R2i(i)*(h(i)-mu2_last)^2;
end
t11=sum(R1i);
t22=sum(R2i);
sigmal_last=sqrt(t1/t11);
sigma2_last=sqrt(t2/t22);

2.6更新两个分布的权重

%Step 5.
%更新权值
w1_last=s11/N;
w2_last=s22/N;

3.结果显示

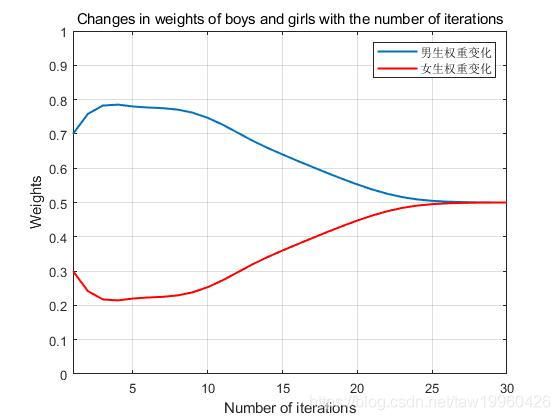
3.1权重随迭代次数变换图

%画出男女生的权重迭代历史
figure(3);
x1=1:0.5:iteration;
y1=interp1(outcome(:,3),x1,'spline');
%interp1用法参考https://www.cnblogs.com/jiahuiyu/articles/4978005.html   
plot(y1,'linewidth',1.5);%画出男生的权重迭代历史
hold on;
grid on;
y2=interp1(outcome(:,6),x1,'spline');
plot(y2,'r','linewidth',1.5);%画出女生权重迭代历史
legend('男生权重变化','女生权重变化','location','northeast');%坐标轴设置，将标识框放置在图的左上角
title('Changes in weights of boys and girls with the number of iterations');
xlabel('Number of iterations');
ylabel('Weights');
axis([1 iteration 0 1]);

3.2男生女生以及混合后身高的概率密度曲线图

figure(4);
hold on;
%男生女生以及混合后身高的概率密度曲线
t=linspace(140,220,550);%500个
%女生的概率密度函数
yy2=normpdf(t,mu2_last,sigma2_last);
plot(t,yy2,'m','linewidth',1.5);
%男生的概率密度函数
yy1=normpdf(t,mu1_last,sigma1_last);
plot(t,yy1,'linewidth',1.5);
y3=w1_last*yy1+w2_last*yy2;
plot(t,y3,'k','linewidth',1.5);
legend('女生','男生','混合');
title('男生女生以及混合后身高的概率密度曲线');
xlabel('身高/cm');ylabel('概率');hold off;%坐标轴设置
hold off;

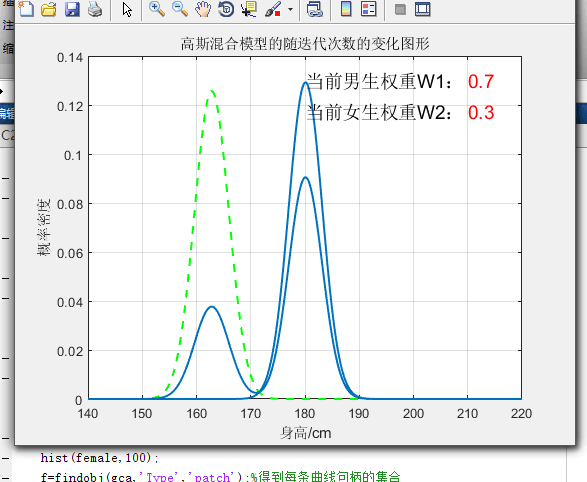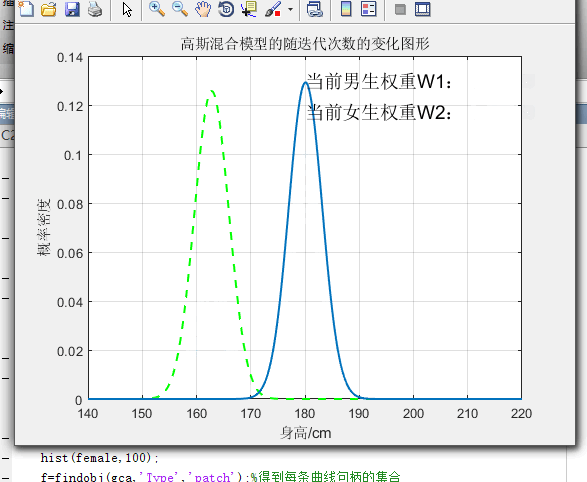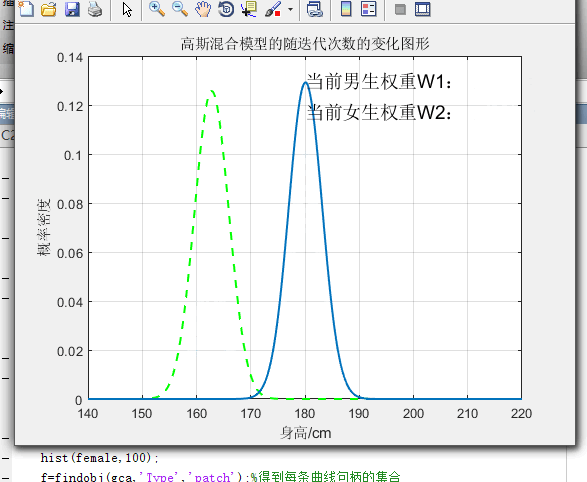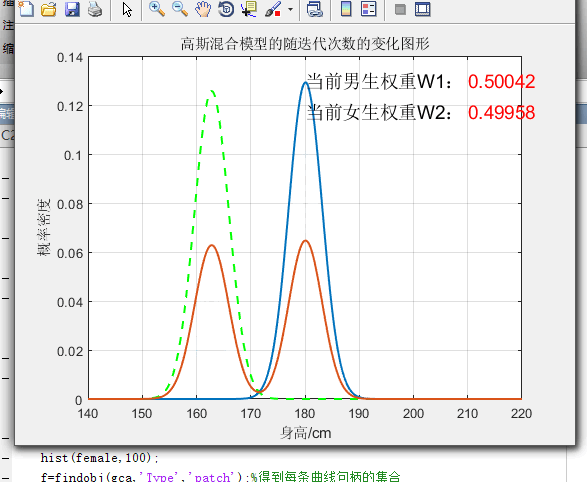
3.3不同权值下图像的比较

%画高斯混合模型的随迭代次数的变化而变化图形
figure(5)
plot(t,yy2,'--g','linewidth',1.5);
hold on;
plot(t,yy1,'linewidth',1.5);
title('高斯混合模型的随迭代次数的变化图形');
xlabel('身高/cm');
ylabel('概率密度');
grid on;
weights1=outcome(:,3);
weights2=outcome(:,6);
%
%将字符串基本信息显示在右上角
text(180,0.13,'当前男生权重W1： ','FontSize',14,'FontWeight','demi');%图中显示权重
text(180,0.117,'当前女生权重W2： ','FontSize',14,'FontWeight','demi');
c=colormap(lines(iteration));%定义times条不同颜色的线条
for i=1:iteration
      pause(0.2);
    %绘制迭代i次的图像,以不同颜色
    y4=weights1(i)*yy1+weights2(i)*yy2;%对两个高斯概率密度图像进行加权
    plt=plot(t,y4,'color',c(i,:),'linewidth',1.5);%绘画加权后的图像
    %weights里面的数值转换为字符串
    str1=num2str(weights1(i));
    str2=num2str(weights2(i));
    %权重跟着i变换
    tex1=text(210,0.13,str1,'FontSize',14,'FontWeight','demi','color','r');%显示当前权重值
    tex2=text(210,0.117,str2,'FontSize',14,'FontWeight','demi','color','r');
    %删除原来的，动态显示
    pause(0.4);
    if(iteration>i)
        delete(tex1);
        delete(tex2);
        delete(plt);
    end
end
hold off;

二、GMM高斯混合模型(python)

1.数据准备

# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
from scipy import stats
import em

#产生身高数据
np.random.seed(100)  # 固定随机数种子，确保下次运行数据相同
#产生满足正太分布的随机数，参数分别为：均值，方差，样本量
male=np.random.normal(180,np.sqrt(10),1000)
female=np.random.normal(163,np.sqrt(10),1000)

2.起始图像显示

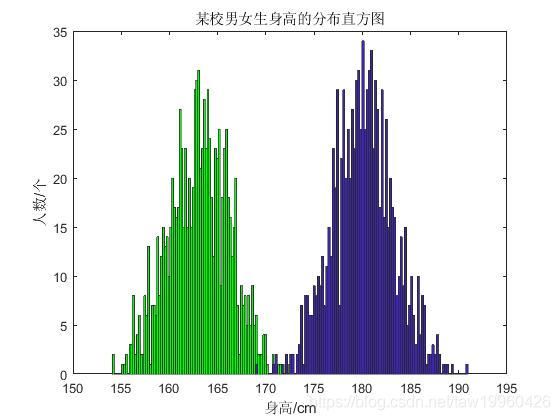
2.1男女生身高的分布直方图

#分别画出男女生图像
m1=pd.Series(male).hist(bins=100)
f1=pd.Series(female).hist(bins=100)
m1.plot()
f1.plot()
plt.title('Histogram of height distribution of boys and girls in a school')
#某校男女生身高的分布直方图
plt.xlabel('height/cm')
plt.ylabel('People/Number')
plt.show()

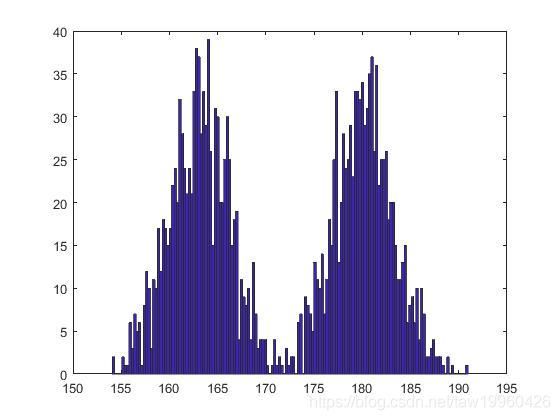
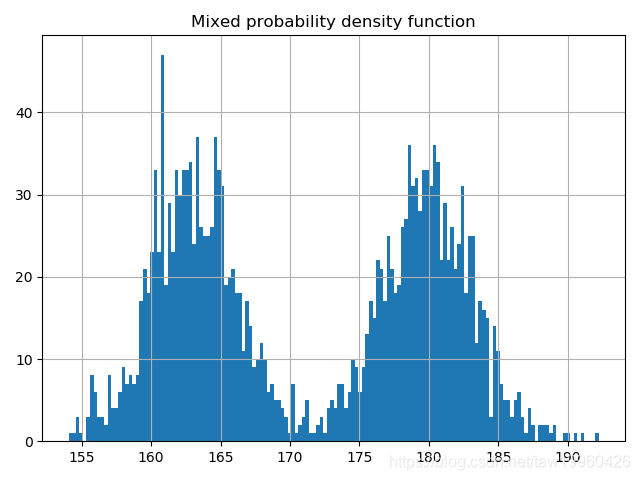
2.2混合数据后画图

#混合数据后画图
h=list(male)# 转化为list
h.extend(female)
h=np.array(h)# 再转成numpy格式的数据
h1=pd.Series(h).hist(bins=150)
h1.plot()
plt.title('Mixed probability density function')#混合后概率密度函数
plt.show()

3.GMM构造

#GMM的构造
#Step 1.首先根据经验来分别对男女生的均值、方差和权值进行初始化
mu1=170;sigmal=10;w1=0.7#男生的
mu2=160;sigma2=10;w2=0.3#以我们学校理工院校为例

d=1
n = len(h)  # 样本长度
# 开始EM算法的主循环
for iteration in range(100):
    mu1,sigmal,w1,mu2,sigma2,w2=em.em(h,mu1,sigmal,w1,mu2,sigma2,w2)

4.最终结果显示

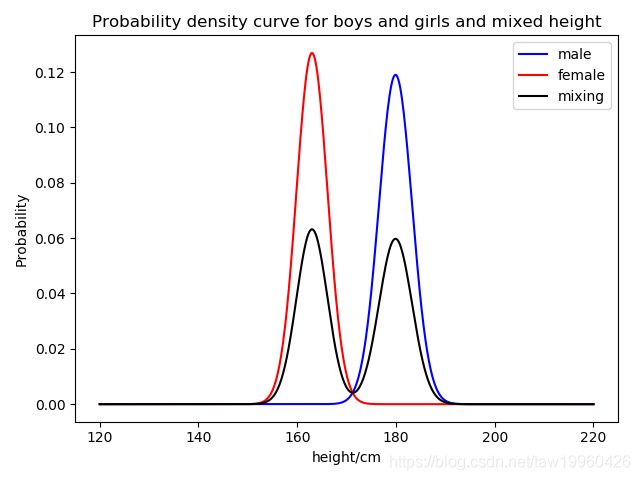
男生女生以及混合后身高的概率密度曲线

#男生女生以及混合后身高的概率密度曲线
t=np.linspace(120,220,550)#500个
m = stats.norm.pdf(t,loc=mu1, scale=sigmal) # 男生分布的预测
f = stats.norm.pdf(t,loc=mu2, scale=sigma2) # 女生分别的预测
mix=w1*m+w2*f#混合后
plt.plot(t, m, color='b')
plt.plot(t, f, color='r')
plt.plot(t, mix, color='k')
#男生女生以及混合后身高的概率密度曲线
plt.title('Probability density curve for boys and girls and mixed height')
#plt.legend([p1,p2,p3],["male","female","mixing"],loc='upper right')
plt.legend(["male","female","mixing"],loc='upper right')
plt.xlabel('height/cm')
plt.ylabel('Probability')#坐标轴设置
plt.show()

权重的迭代情况：