神经网络:卷积神经网络基础学习
1、卷积神经的由来
1.1 引言
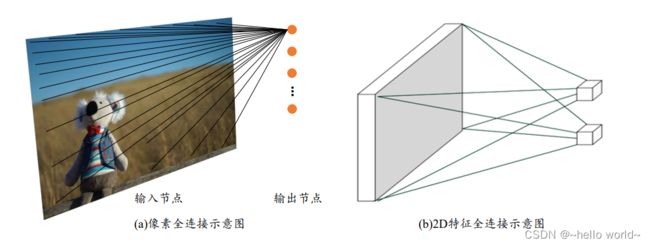
全连接层也称为稠密连接层(Dense Layer),网络层的每个输出节点都与所有的输入节点相连接,用于提取所有输入节点的特征信息,这种稠密的连接方式全连接层参数量大、计算代价高。输出与输入的关系为:

全连接网络因参数量过大运算时所占计算机资料较大,为解决这个问题,提出了局部相关性。局部相关性,是基于距离的重要性分布假设特性,即只关注和自己距离较近的部分节点,而忽略距离较远的节点。在这种重要性分布假设下,全连接层的连接模式变成了输出节点 只与以 为中心的局部区域(感受野)相连接,与其它像素无连接。
以2D 图片数据为例,如果简单地认为与当前像素欧式距离小于和等于 k √ 2 \frac{k}{√2} √2k 的像素点重要性较高,欧式距离大于 k √ 2 \frac{k}{√2} √2k 到像素点重要性较低,那么就很轻松地简化了每个像素点的重要性分布问题。

如图所示,以实心网格所在的像素为参考点,它周边欧式距离小于或等于 k √ 2 \frac{k}{√2} √2k 的像素点以矩形网格表示,网格内的像素点重要性较高,网格外的像素点较低。这个高宽为的窗口称为感受野(Receptive Field),它表征了每个像素对于中心像素的重要性分布情况,网格内的像素才会被考虑,网格外的像素对于中心像素会被忽略。
利用局部相关性的思想,我们把感受野窗口的高、宽记为(感受野的高、宽可以不相等,为了便与表达,这里只讨论高宽相等的情况),当前位置的节点与大小为 的窗口内的所有像素相连接,与窗口外的其它像素点无关,此时网络层的输入输出关系表达如下:
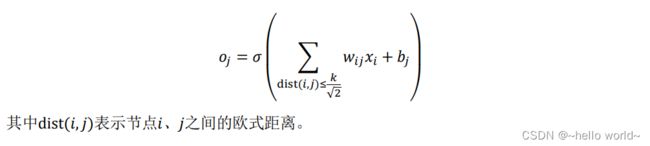
.
1.2 权值共享
每个输出节点仅与感受野区域内 × 个输入节点相连接,输出层节点数为 ‖‖,则当前层的参数量为 × × ‖‖,相对于全连接层的 ‖‖ × ‖‖,考虑到一般取值较小,如 1、3、5 等, × ≪ ‖‖,因此成功地将参数量减少了很多。能否再将参数量进一步减少,比如只需要 × 个参数即可完成当前层的计算?
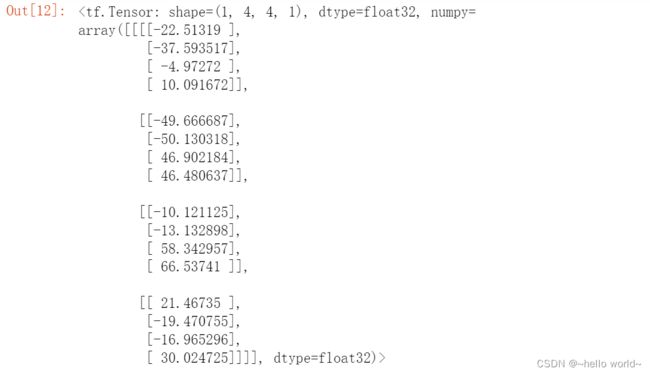
通过权值共享的思想,对于每个输出节点 ,均使用相同的权值矩阵 ,那么无论输出节点的数量 ‖‖ 是多少,网络层的参数量总是 × 。如图所示,在计算左上角位置的输出像素时,使用权值矩阵:
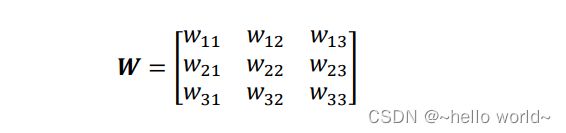
与对应感受野内部的像素相乘累加,作为左上角像素的输出值;在计算右下方感受野区域时,共享权值参数,即使用相同的权值参数相乘累加,得到右下角像素的输出值,此时网络层的参数量只有3 × 3 = 9个,且与输入、输出节点数无关。

通过运用局部相关性和权值共享的思想,成功把网络的参数量从 ‖‖ × ‖‖ 减少到 × (准确地说,是在单输入通道、单卷积核的条件下)。这种共享权值的 “局部连接层” 网络其实就是卷积神经网络。
.
1.3 卷积运算
在局部相关性的先验下,提出了简化的 “局部连接层”,对于窗口 × 内的所有像素,采用权值相乘累加的方式提取特征信息,每个输出节点提取对应感受野区域的特征信息。这种运算其实是信号处理领域的一种标准运算:离散卷积运算。离散卷积运算在计算机视觉中有着广泛的应用,这里给出卷积神经网络层从数学角度的阐述。在信号处理领域,1D 连续信号的卷积运算被定义两个函数的积分:函数 ()、函数 (),其中 () 经过了翻转 (−) 和平移后变成 ( − ) 。卷积的“卷”是指翻转平移操作,“积”是指积分运算
1D 连续卷积定义为:
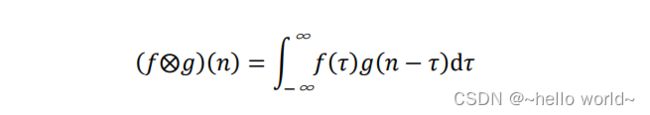
离散卷积定义:
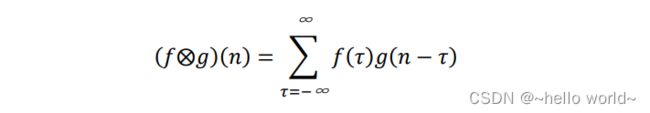
1.4 2D 离散卷积运算
在计算机视觉中,卷积运算基于 2D 图片函数 ( ) 和 2D 卷积核 ( ),其中 ( ) 和 ( ) 仅在各自窗口有效区域存在值,其它区域视为 0,如图 所示,则 2D 离散卷积定义为:
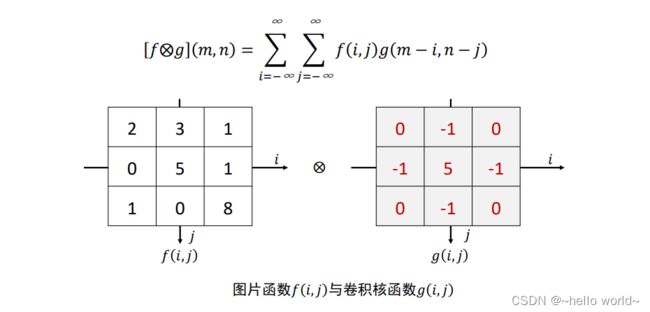
2D 离散卷积运算是先将卷积核( )函数翻转(沿着和方向各翻转一次),变成 (− −) 。当 ( ) = (−1, −1 ) 时,(− 1− , −1 − )表示卷积核函数翻转后再向左、向上各平移一个单元,此时:
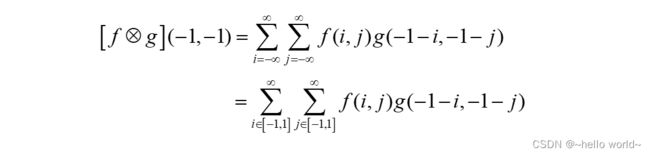
2D 函数只在 ∈ [−1,1], ∈ [−1,1] 存在有效值,其它位置为 0。按照计算公式,我们可以得到 [⨂] ( 0,−1 ) =7 ,如下图所示:
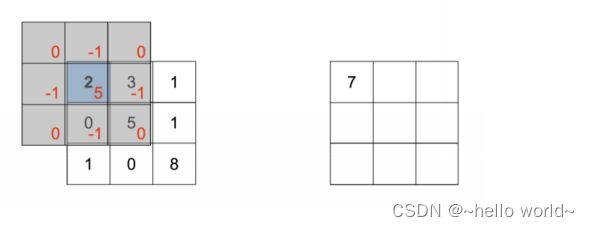
.
同理,( ) = ( 0,−1)时:
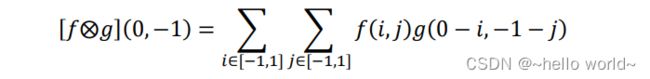
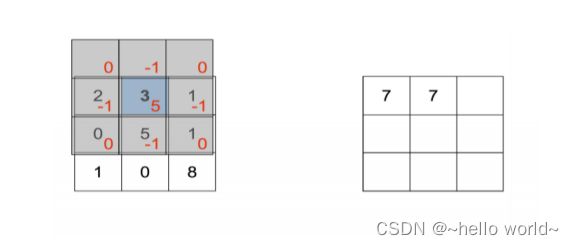
即卷积核翻转后再向上平移一个单元后对应位置相乘累加, [⨂] (0,−1) =7,如图所示
.
当( ) = (1,−1)时:
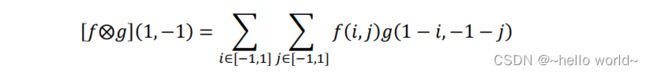
即卷积核翻转后再向右、向上各平移一个单元后对应位置相乘累加,[⨂] (0,−1) =1,如图所示。
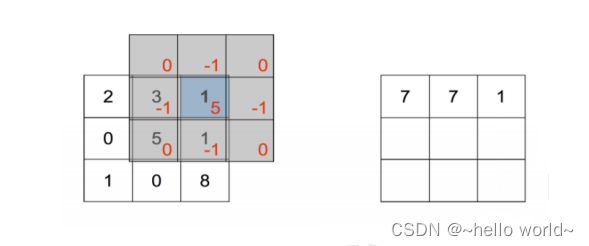
.
当( ) = (−1,0)时:
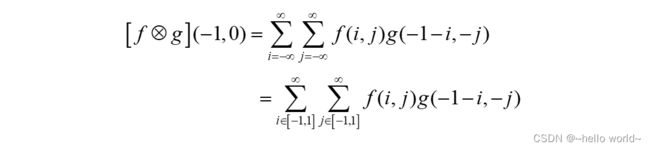
即卷积核翻转后再向左平移一个单元后对应位置相乘累加,[⨂] (0,−1) =1, 如图所示
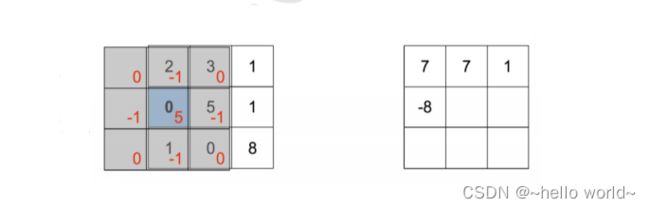
.
按照此种方式循环计算,可以计算出函数 [⨂] (,), ∈[−1,1], ∈ [−1,1] 的所有值,如下图所示
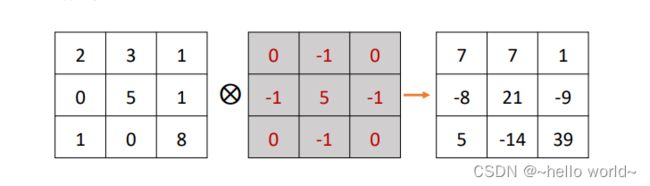
.
我们把“权值相乘累加”的运算记为 ∙(,):
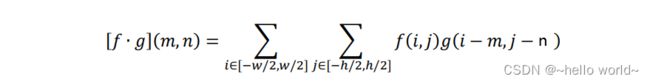
仔细比较它与标准的 2D 卷积运算不难发现,在“权值相乘累加”中的卷积核函数 ( ),并没有经过翻转。只不过对于神经网络来说,目标是学到一个函数 ( ) 使得 ℒ 越小越好,至于 ( ) 是不是恰好就是卷积运算中定义的“卷积核”函数并不十分重要,因为并不会直接利用它。在深度学习中,函数 ( ) 统一称为卷积核(Kernel),有时也叫 Filter、Weight 等。由于始终使用 ( ) 函数完成卷积运算,卷积运算其实已经实现了权值共享的思想。
2D 离散卷积运算流程:每次通过移动卷积核,并与图片对应位置处的感受野像素相乘累加,得到此位置的输出值。卷积核即是行、列为大小的权值矩阵,对应到特征图上大小为 的窗口即为感受野,感受野与权值矩阵 相乘累加,得到此位置的输出值。通过权值共享,从左上方逐步向右、向下移动卷积核,提取每个位置上的像素特征,直至最右下方,完成卷积运算。可以看出,两种理解方式殊途同归,从数学角度理解,卷积神经网络即是完成了 2D 函数的离散卷积运算;从局部相关与权值共享角度理解,也能得到一样的效果。正是基于卷积运算,卷积神经网络才能如此命名。
在计算机视觉领域,2D 卷积运算能够提取数据的有用特征,通过特定的卷积核与输入图片进行卷积运算,获得不同特征的输出图片,如下表所示,列举了一些常见的卷积
核及其效果样片。

.
2、卷积神经网络
卷积神经网络通过充分利用局部相关性和权值共享的思想,大大地减少了网络的参数量,从而提高训练效率,更容易实现超大规模的深层网络。
以 2D 图片数据为例,对卷积神经网络层的具体计算流程展开说明。卷积层接受高、宽分别为 ℎ、,通道数为 的输入特征图,在 个高、宽都为,通道数为 的卷积核作用下,生成高、宽分别为 ℎ′、′,通道数为 的特征图输出。需要注意的是,卷积核的高宽可以不等,为了简化讨论,这里仅讨论高宽都为的情况,之后可以轻松推广到高、宽不等的情况。首先从单通道输入、单卷积核的情况开始讨论,然后推广至多通道输入、单卷积核,最后讨论最常用,也是最复杂的多通道输入、多个卷积核的卷积层实现。
.
2.1 基础概念介绍
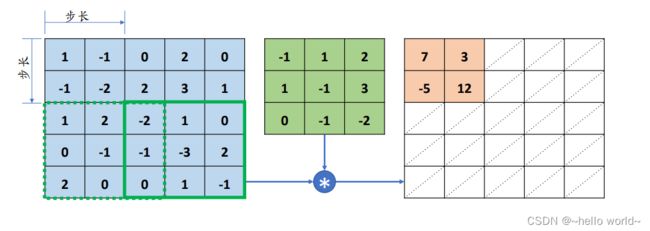
步长:
感受野密度的控制手段一般是通过移动步长(Strides)实现的。步长是指感受野窗口每次移动的长度单位,对于 2D 输入来说,分为沿 (向右)方向和 (向下)方向的移动长度。如下图 所示,感受野步长为 2 。
.
填充
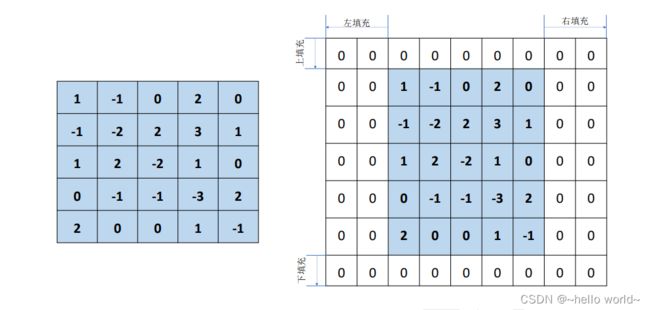
由上图可知,经过卷积运算后的输出 的高宽一般会小于输入 的高宽,即使是步长 = 1 时,输出 的高宽也会略小于输入 高宽。在网络模型设计时,有时希望输出的高宽能够与输入 的高宽相同,从而方便网络参数的设计、残差连接等。为了让输出 的高宽能够与输入 的相等,一般通过在原输入 的高和宽维度上面进行填充(Padding)若干无效元素操作,得到增大的输入′。通过精心设计填充单元的数量,在′上面进行卷积运算得到输出的高宽可以和原输入相等,甚至更大。
如下图所示,在高/行方向的上(Top)、下(Bottom)方向,宽/列方向的左(Left)、右(Right)均可以进行不定数量的填充操作,填充的数值一般默认为 0,也可以填充自定义的数据。上、下方向各填充 1 行,左、右方向各填充 2 列,得到新的输入′。
.
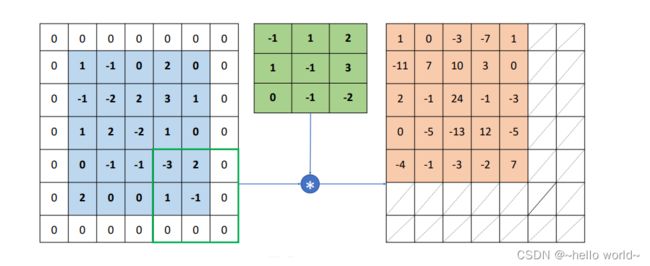
通过精心设计的 Padding 方案,可以得到输出 和输入 的高、宽相等的结果,如下图
.
卷积神经层的输出尺寸 [b,ℎ′,′, ] 由卷积核的数量 ,卷积核的大小 ,步长 ,填充数 (只考虑上下填充数量 ℎ 相同,左右填充数量 相同的情况) 以及输入 的高宽 ℎ/ 共同决定,它们之间的数学关系可以表达为:
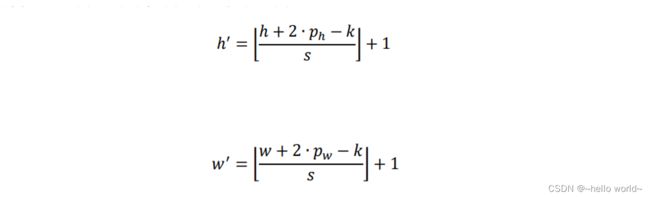
其中 ℎ、 分别表示高、宽方向的填充数量,⌊∙⌋表示向下取整。在 TensorFlow 中,在 = 1 时,如果希望输出 和输入 高、宽相等,只需要简单地设置参数 padding=”SAME” 即可使 TensorFlow 自动计算 padding 数量,非常方便。
.
2.2 单通道输入和单卷积核
单通道情况下输入 = 1,如灰度图片只有灰度值一个通道,单个卷积核 = 1 的情况。以输入 为 5×5 的矩阵,卷积核为 3×3 的矩阵为例。与卷积核同大小的感受野(输入上方的绿色方框)首先移动至输入最左上方,选中输入 上 3×3 的感受野元素,与卷积核(图片中间3 × 3方框)对应元素相乘:
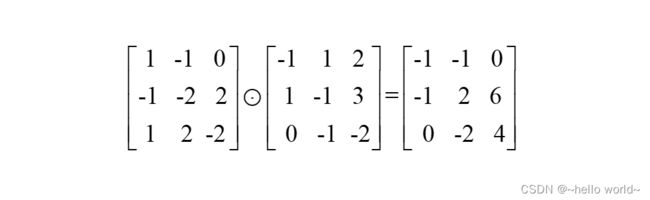
⨀符号表示哈达马积(Hadamard Product),即矩阵的对应元素相乘,它与矩阵相乘符号@是矩阵的二种最为常见的运算形式。运算后得到3 × 3的矩阵,这 9 个数值全部相加得到标量 7,写入输出矩阵第一行、第一列的位置,如图所示。
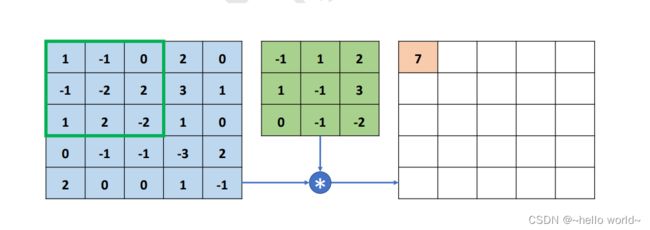
.
完成第一个感受野区域的特征提取后,感受野窗口向右移动一个步长单位(Strides,记为 ,默认为 1),选中下图中绿色方框中的 9 个感受野元素,按照同样的计算方法,与卷积核对应元素相乘累加,得到输出 10,写入第一行、第二列位置。
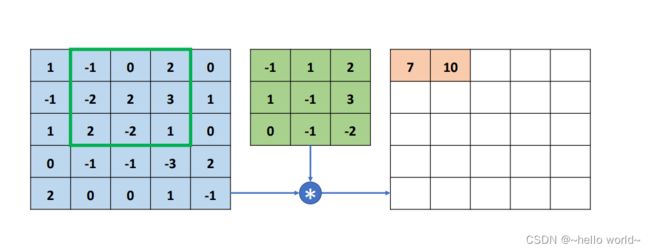
.
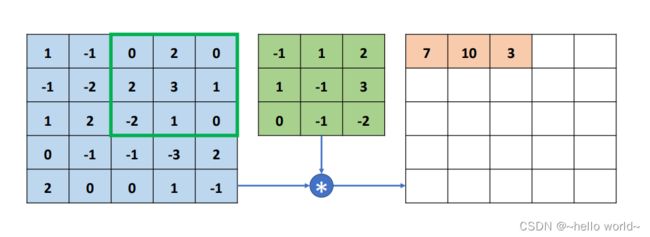
感受野窗口再次向右移动一个步长单位,选中下图中绿色方框中的元素,并与卷积核相乘累加,得到输出 3,并写入输出的第一行、第三列位置。
.
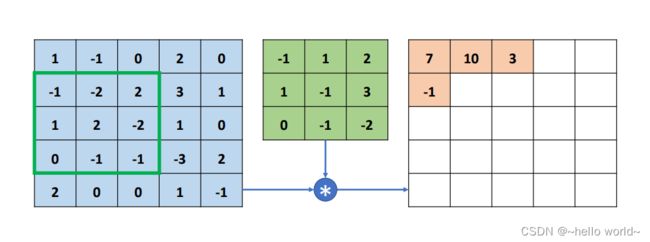
若感受野已移动至输入 的有效像素的最右边,无法向右边继续移动(在不填充无效元素的情况下),因此感受野窗口向下移动一个步长单位 ( =1),并回到当前行的行首位置,继续选中新的感受野元素区域,与卷积核运算得到输出-1。此时的感受野由于经过向下移动一个步长单位,因此输出值-1 写入第二行、第一列位置。
.
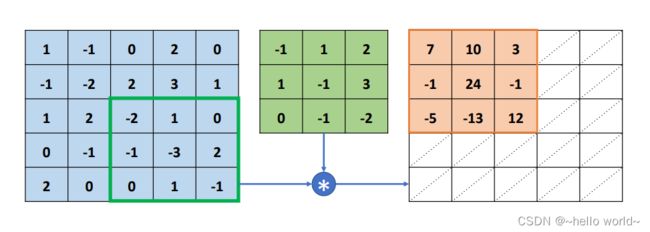
按照上述方法,每次感受野向右移动 = 1 个步长单位,若超出输入边界,则向下移动 = 1 个步长单位,并回到行首,直到感受野移动至最右边、最下方位置。每次选中的感受野区域元素,和卷积核对应元素相乘累加,并写入输出的对应位置。最终输出得到一个 3×3 的矩阵,比输入 5×5 略小,这是因为感受野不能超出元素边界的缘故。可以观察到,卷积运算的输出矩阵大小由卷积核的大小 ,输入 的高宽 ℎ,,移动步长 ,是否填充等因素共同决定。
.
2.3 多通道输入和单卷积核
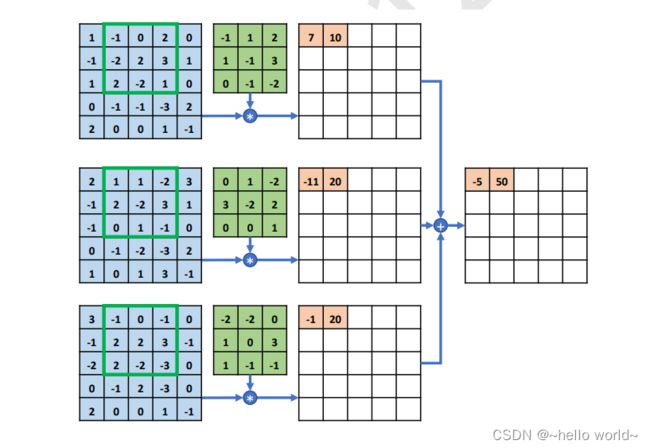
多通道输入的卷积层更为常见,比如彩色的图片包含了 R/G/B 三个通道,每个通道上面的像素值表示 R/G/B 色彩的强度。以 3 通道输入、单个卷积核为例,将单通道输入的卷积运算方法推广到多通道的情况。
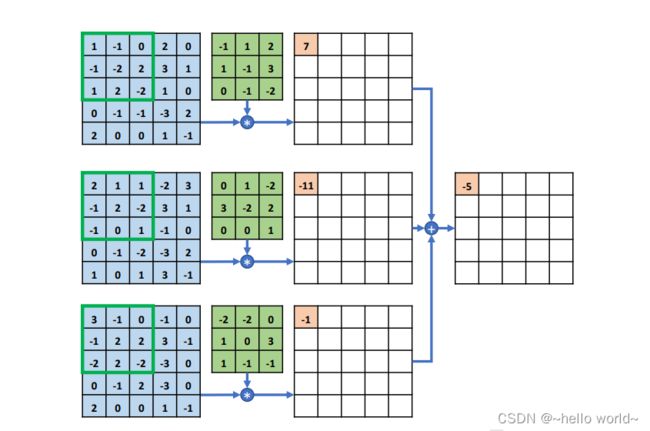
如图所示,每行的最左边 5×5 的矩阵表示输入 的 1~ 3 通道,第 2 列的 3×3 矩阵分别表示卷积核的 1~3 通道,第 3 列的矩阵表示当前通道上运算结果的中间矩阵,最右边一个矩阵表示卷积层运算的最终输出。
在多通道输入的情况下,卷积核的通道数需要和输入 的通道数量相匹配,卷积核的第 个通道和 的第 个通道运算,得到第 个中间矩阵,此时可以视为单通道输入与单卷积核的情况,所有通道的中间矩阵对应元素再次相加,作为最终输出。
.
感受野窗口同步在 的每个通道上向右移动 = 1 个步长单位,此时感受野区域元素如下图,每个通道上面的感受野与卷积核对应通道上面的矩阵相乘累加,得到中间变量 10、20、20,全部相加得到输出 50,写入第一行、第二列元素位置。
.
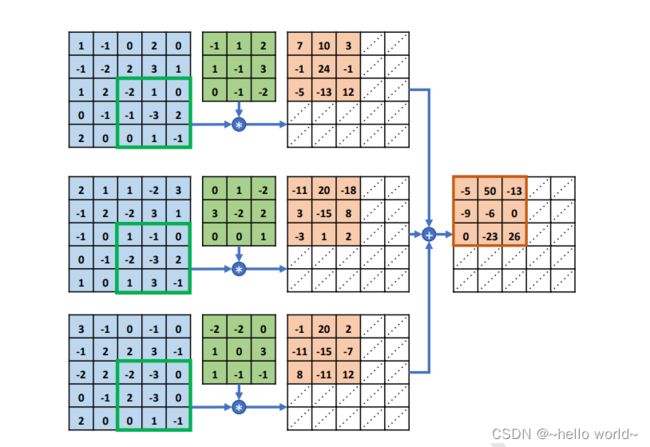
以此方式同步移动感受野窗口,直至最右边、最下方位置,此时全部完成输入和卷积核的卷积运算,得到 3 × 3 的输出矩阵,如图所示。
.
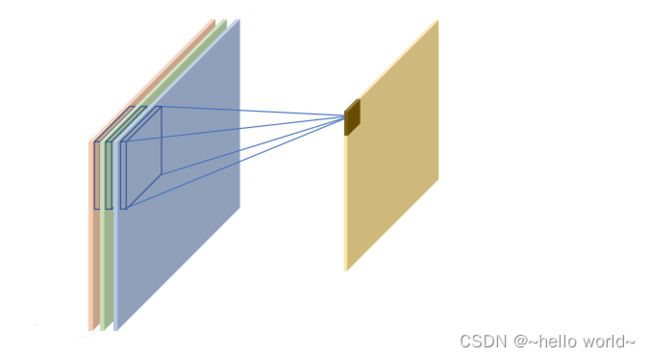
整个的计算示意图如下图所示,输入的每个通道处的感受野均与卷积核的对应通道相乘累加,得到与通道数量相等的中间变量,这些中间变量全部相加即得到当前位置的输出值。输入通道的通道数量决定了卷积核的通道数。一个卷积核只能得到一个输出矩阵,与输入的通道数量无关。
.
2.4 多通道输入、多卷积核
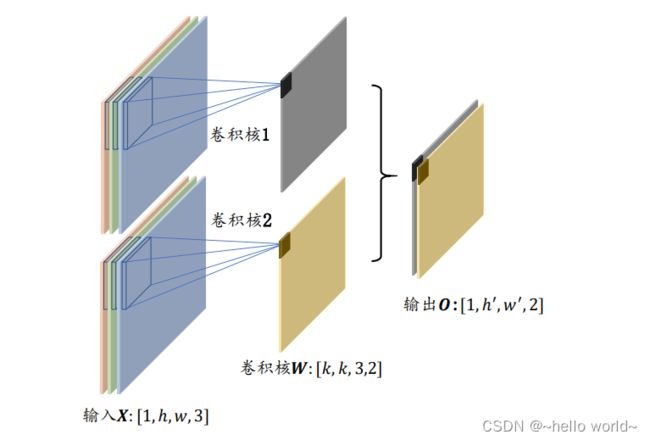
多通道输入、多卷积核是卷积神经网络中最为常见的形式。当出现多卷积核时,第 ( ∈ [1,] ,为卷积核个数) 个卷积核与输入 运算得到第 个输出矩阵(也称为输出张量 的通道 ),最后全部的输出矩阵在通道维度上进行拼接(Stack 操作,创建输出通道数的新维度),产生输出张量 , 包含了 个通道数。
以 3 通道输入、2 个卷积核的卷积层为例。第一个卷积核与输入 运算得到输出 的第 一个通道,第二个卷积核与输入 运算得到输出 的第二个通道,如下图 ;输出的两个通道拼接在一起形成了最终输出 。每个卷积核的大小 、步长 、填充设定等都是统一设置,这样才能保证输出的每个通道大小一致,从而满足拼接的条件。
.
3、卷积层实现
在 TensorFlow 中,既可以通过自定义权值的底层实现方式搭建神经网络,也可以直接调用现成的卷积层类的高层方式快速搭建复杂网络。
3.1 自定义权值
在 TensorFlow 中,通过 tf.nn.conv2d 函数可以方便地实现 2D 卷积运算。tf.nn.conv2d 基于输入: [ b ℎ ] 和卷积核: [ ] 进行卷积运算,得到输出 : [ b ℎ′ ′ ] ,其中 表示输入通道数, 表示卷积核的数量,也是输出特征图的通道数。例如:
# 模拟输入,高宽为 5,通道为3
x = tf.random.normal([2,5,5,3])
# 创建 W 张量,4 个 3x3 大小卷积核
w = tf.random.normal([3,3,3,4])
# 步长为 1, padding 为 0,
out = tf.nn.conv2d(x,w,strides=1,padding=[[0,0],[0,0],[0,0],[0,0]])
print(out.shape) #====> (2, 3, 3, 4)
其中 padding 参数的设置格式为:padding=[[0,0],[上,下],[左,右],[0,0]]
例如:[ [0,0], [1,1], [1,1], [0,0] ]表示上下左右各填充一个单位
.
特别地,通过设置参数 padding=‘SAME’、strides=1 可以直接得到输入、输出同大小的卷积层,其中 padding 的具体数量由 TensorFlow 自动计算并完成填充操作。例如:
x = tf.random.normal([2,5,5,3])
w = tf.random.normal([3,3,3,4])
# 设置为输出、输入同大小, 需要注意的是, padding=same 只有在 strides=1 时才是同大小
out = tf.nn.conv2d(x,w,strides=1,padding='SAME')
print(out.shape) #====> (2, 5, 5, 4)
.
当 > 1 时,设置 padding='SAME’将使得输出高、宽将成 = 1 s \frac{1}{s} s1 倍地减少
x = tf.random.normal([2,5,5,3])
w = tf.random.normal([3,3,3,4])
# 高宽先 padding 成可以整除 3 的最小整数 6,然后 6 按 3 倍减少,得到 2x2
out = tf.nn.conv2d(x,w,strides=3,padding='SAME')
print(out.shape) #====> (2, 2, 2, 4)
.
卷积神经网络层与全连接层一样,可以设置网络带偏置向量。tf.nn.conv2d 函数是没有实现偏置向量计算的,添加偏置只需要手动累加偏置张量即可。例如:
# 根据[cout]格式创建偏置向量
b = tf.zeros([4])
# 在卷积输出上叠加偏置向量,它会自动 broadcasting 为[b,h',w',cout]
out = out + b
3.2 卷积层类
通过卷积层类 layers.Conv2D 可以不需要手动定义卷积核 和偏置 张量,直接调用类实例即可完成卷积层的前向计算,实现更加高层和快捷。使用类方式会 (在创建类时或 build 时) 自动创建需要的权值张量和偏置向量等,用户不需要记忆卷积核张量的定义格式,因此使用起来更简单方便,但是灵活性也略低。函数方式的接口需要自行定义权值和偏置等,更加灵活和底层。
在新建卷积层类时,只需要指定卷积核数量参数 filters,卷积核大小 kernel_size,步长strides,填充 padding 等即可。如下创建了 4 个3 × 3大小的卷积核的卷积层,步长为 1,padding 方案为’SAME’:
layer = layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME'
如果卷积核高宽不等,步长行列方向不等,此时需要将 kernel_size 参数设计为 tuple 格式(ℎ ),strides 参数设计为(ℎ )。如下创建 4 个 3×3 大小的卷积核,竖直方向移动步长ℎ = 2,水平方向移动步长 = 1:
layer = layers.Conv2D(4,kernel_size=(3,4),strides=(2,1),padding='SAME')
创建完成后,通过调用实例(的__call__方法)即可完成前向计算,例如:
import tensorflow as tf
from tensorflow.keras import layers
# 创建卷积层类
layer = layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME')
# 前向计算
out = layer(x)
print(out.shape) # 输出张量的 shape======>(2, 5, 5, 4)
在类 Conv2D 中,保存了卷积核张量 和偏置 ,可以通过类成员 trainable_variables 直接返回 和 的列表。通过调用 layer.trainable_variables 可以返回 Conv2D 类维护的 和 张量,这个类成员在获取网络层的待优化变量时非常有用。也可以直接调用类实例 layer.kernel、layer.bias 名访问和张量。例如:
# 返回所有待优化张量列表
layer.trainable_variables
.
3.3 LeNet-5 实战
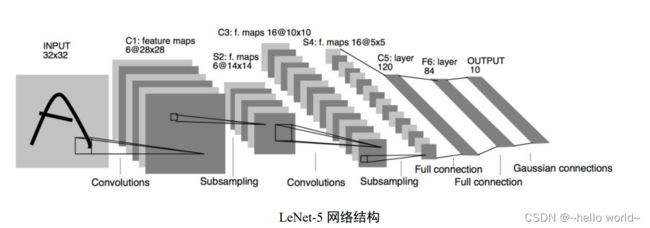
LeNet-5 用于手写数字和机器打印字符图片识别的神经网络。 LeNet-5 的网络结构图如下,它接受 32×32 大小的数字、字符图片,经过第一个卷积层得到 [b 28 28 6] 形状的张量,经过一个向下采样层,张量尺寸缩小到 [b 14 14 6] ,经过第二个卷积层,得到 [b 10 10 16] 形状的张量,同样经过下采样层,张量尺寸缩小到 [b 5 5 16],在进入全连接层之前,先将张量打成 [ b 400] 的张量,送入输出节点数分别为 120、84 的 2 个全连接层,得到 [b 84] 的张量,最后通过 Gaussian connections 层。
LeNet-5 网络层数较少(2 个卷积层和 2 个全连接层),在 LeNet-5 的基础上进行了少许调整,使得它更容易在现代深度学习框架上实现。首先,将输入 形状由 32×32 调整为 28×28,然后将 2 个下采样层实现为最大池化层(降低特征图的高、宽),最后利用全连接层替换掉 Gaussian connections层。网络结构图如下图 :
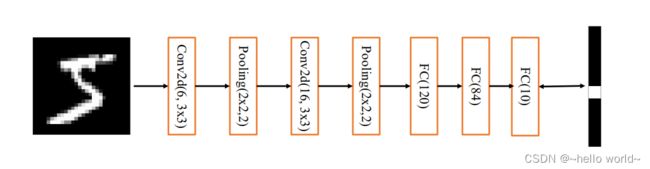
3.3.1 通过 Sequential 容器创建 LeNet-5
from tensorflow import keras
from tensorflow.keras import layers,Sequential
# 通过 Sequential 容器创建 LeNet-5
network = Sequential([# 网络容器
layers.Conv2D(6,kernel_size=3,strides=1), # 第一个卷积层, 6 个 3x3 卷积核
layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
layers.ReLU(), # 激活函数
layers.Conv2D(16,kernel_size=3,strides=1), # 第二个卷积层, 16 个 3x3 卷积核
layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
layers.ReLU(), # 激活函数
layers.Flatten(), # 打平层,方便全连接层处理
layers.Dense(120, activation='relu'), # 全连接层,120 个节点
layers.Dense(84, activation='relu'), # 全连接层,84 节点
layers.Dense(10) # 全连接层,10 个节点
])
# build一次网络模型,给输入 X 的形状,其中4为随意给的 batchsize
network.build(input_shape=(4, 28, 28, 1))
.
通过 summary()函数统计出每层的参数量,打印出网络结构信息和每层参数量详情。
# 统计网络信息
network.summary()

可以看到,卷积层的参数量非常少,主要的参数量集中在全连接层。由于卷积层将输入特征维度降低很多,从而使得全连接层的参数量不至于过大,因此通过卷积神经网络可以显著降低网络参数量,同时增加网络深度。
3.3.2 训练 LeNet-5
在训练阶段,首先将数据集中 shape 为 28×28 的输入 增加一个维度,调整 shape 为 28×28 ,送入模型进行前向计算,得到输出张量 output,shape 为 [b 10] 。我们新建交叉熵损失函数类 (损失函数也能使用类方式) 用于处理分类任务,通过设定from_logits=True 标志位将 softmax 激活函数实现在损失函数中,不需要手动添加损失函数,提升数值计算稳定性。代码如下:
# 创建损失函数类
criteon = losses.CategoricalCrossentropy(from_logits=True)
# w = w - lr * grad
# 学习率的设置,更新参数
optimizers = optimizers.Adam(learning_rate=1e-3)
# 模型训练
for epoch in range(5):
for step, (x, y) in enumerate(train_db):
with tf.GradientTape() as tape:
# 插入通道维度 =>[b,28,28,1]
x = tf.expand_dims(x, axis=3)
# 向前计算,获得10类的概率分布,[b,784]-> [b,10]
out = network(x)
# 真实标签 one-hot 编码, [b] => [b, 10]
y_onehot = tf.one_hot(y, depth=10)
# 计算交叉熵损失函数,标量
loss = criteon(y_onehot, out)
# 自动计算梯度
grads = tape.gradient(loss, network.trainable_variables)
# 自动跟新参数
optimizers.apply_gradients(zip(grads, network.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'loss', float(loss))
3.3.3 模型测试
# 测试集,记录预测正确的数量,总样本数量
total_correct, total = 0, 0
for x, y in test_db:
# 插入通道维数
x = tf.expand_dims(x, axis=3)
# 前向计算,获得 10 类别的预测分布, [b, 784] => [b, 10]
out = network(x)
# 将输出结果归一化处理,得到和为1的概率
prob = tf.nn.softmax(out, axis=1) # [0,1]
# 找到对应维度最大值的索引位置
pred = tf.argmax(prob, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# pred:[b]
# y: [b]
# correct: [b], True(1): equal; False(0): not equal
correct = tf.equal(pred, y)
correct = tf.reduce_sum(tf.cast(correct, dtype=tf.int32))
# 预测对的数量
total_correct += int(correct)
# 统计预测样本总数
total += x.shape[0]
# acc
print('acc:', total_correct / total)
3.3.4 完整代码
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers, optimizers, Sequential, losses
# 预处理 将浮点张量 x 限制在[-1,1]的范围内
def preprocess(x, y):
# x :[-1,1]
x = 2 * tf.cast(x, dtype=tf.float32) / 255 - 1
y = tf.cast(y, dtype=tf.int32)
return x, y
# 加载数据集
(x, y), (x_text, y_text) = datasets.mnist.load_data()
# 创建batch
train_db = tf.data.Dataset.from_tensor_slices((x, y))
train_db = train_db.map(preprocess).shuffle(1000).batch(128)
test_db = tf.data.Dataset.from_tensor_slices((x, y))
test_db = test_db.map(preprocess).batch(128)
# 通过 Sequential 容器创建 LeNet-5
network = Sequential([# 网络容器
layers.Conv2D(6,kernel_size=3,strides=1), # 第一个卷积层, 6 个 3x3 卷积核
layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
layers.ReLU(), # 激活函数
layers.Conv2D(16,kernel_size=3,strides=1), # 第二个卷积层, 16 个 3x3 卷积核
layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
layers.ReLU(), # 激活函数
layers.Flatten(), # 打平层,方便全连接层处理
layers.Dense(120, activation='relu'), # 全连接层,120 个节点
layers.Dense(84, activation='relu'), # 全连接层,84 节点
layers.Dense(10) # 全连接层,10 个节点
])
# build 一次网络模型,给输入 X 的形状,其中 4 为随意给的 batchsz
network.build(input_shape=(4, 28, 28, 1))
# 统计网络信息
network.summary()
# 创建损失函数类
criteon = losses.CategoricalCrossentropy(from_logits=True)
# w = w - lr * grad
# 学习率的设置,更新参数
optimizers = optimizers.Adam(learning_rate=1e-3)
# 模型训练
for epoch in range(5):
for step, (x, y) in enumerate(train_db):
with tf.GradientTape() as tape:
# 插入通道维度 =>[b,28,28,1]
x = tf.expand_dims(x, axis=3)
# 向前计算,获得10类的概率分布,[b,784]-> [b,10]
out = network(x)
# 真实标签 one-hot 编码, [b] => [b, 10]
y_onehot = tf.one_hot(y, depth=10)
# 计算交叉熵损失函数,标量
loss = criteon(y_onehot, out)
# 自动计算梯度
grads = tape.gradient(loss, network.trainable_variables)
# 自动跟新参数
optimizers.apply_gradients(zip(grads, network.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'loss', float(loss))
# 测试集,记录预测正确的数量,总样本数量
total_correct, total = 0, 0
for x, y in test_db:
# 插入通道维数
x = tf.expand_dims(x, axis=3)
# 前向计算,获得 10 类别的预测分布, [b, 784] => [b, 10]
out = network(x)
# 将输出结果归一化处理,得到和为1的概率
prob = tf.nn.softmax(out, axis=1) # [0,1]
# 找到对应维度最大值的索引位置
pred = tf.argmax(prob, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# pred:[b]
# y: [b]
# correct: [b], True(1): equal; False(0): not equal
correct = tf.equal(pred, y)
correct = tf.reduce_sum(tf.cast(correct, dtype=tf.int32))
# 预测对的数量
total_correct += int(correct)
# 统计预测样本总数
total += x.shape[0]
# acc
print('acc:', total_correct / total)
4、梯度传播
我们知道,卷积层通过移动感受野的方式实现离散卷积操作,那么它的梯度传播是怎么进行的呢?
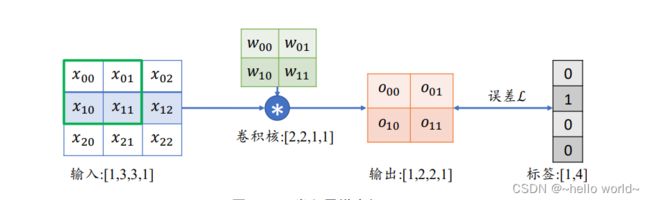
考虑一简单的情形:输入为 3×3 的单通道矩阵,与一个 2×2 的卷积核,进行卷积运算,输出结果打平后直接与虚构的标注计算误差,如下图。
首先推导出输出张量的表达形式:
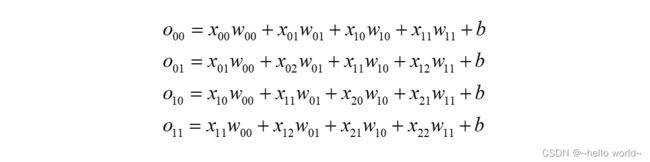
以00 的梯度计算为例,通过链式法则分解:
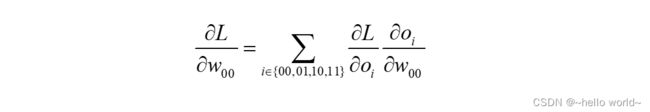

同理得:
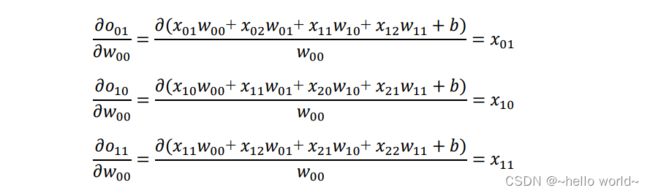
可以观察到,通过循环移动感受野的方式并没有改变网络层可导性,同时梯度的推导也并不复杂,只是当网络层数增大以后,人工梯度推导将变得十分的繁琐。不过不需要担心,深度学习框架可以帮我们自动完成所有参数的梯度计算与更新,我们只需要设计好网络结构即可。
5、池化层
在卷积层中,可以通过调节步长参数 实现特征图的高宽成倍缩小,从而降低了网络的参数量。实际上,除了通过设置步长,还有一种专门的网络层可以实现尺寸缩减功能,它就是池化层(Pooling Layer)。
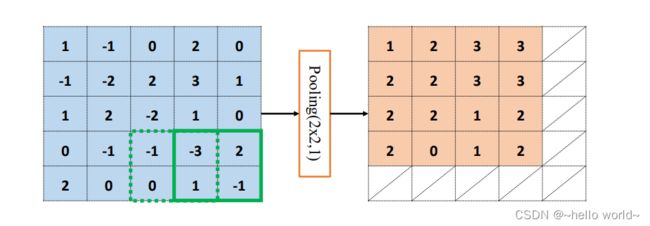
池化层同样基于局部相关性的思想,通过从局部相关的一组元素中进行采样或信息聚合,从而得到新的元素值。特别地,最大池化层(Max Pooling)从局部相关元素集中选取最大的一个元素值,平均池化层(Average Pooling)从局部相关元素集中计算平均值并返回。以 5×5 输入 的最大池化层为例,考虑池化感受野窗口大小 =2,步长 =1 的情况,如下图 。绿色虚线方框代表第一个感受野的位置,感受野元素集合为 1 , − 1 , − 1 , − 2 {1,-1,-1,-2} 1,−1,−1,−2
在最大池化采样的方法下 ′ = max({ 1,-1,-1,-2})=1
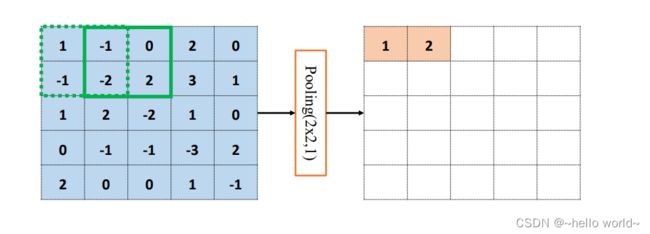
同当逐渐移动感受野窗口至最右边,此时窗口已经到达输入边缘,按照卷积层同样的方式,感受野窗口向下移动一个步长,并回到行首,如下图:
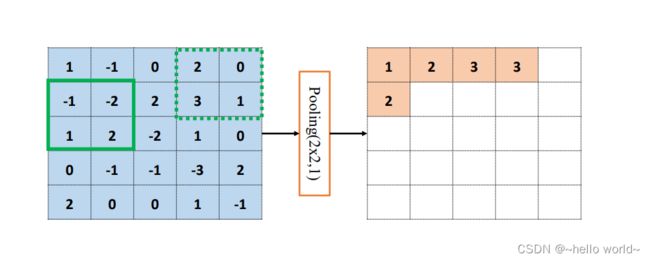
循环往复,直至最下方、最右边,获得最大池化层的输出,长宽为 4×4,略小于输入 的高宽,如下图:
.
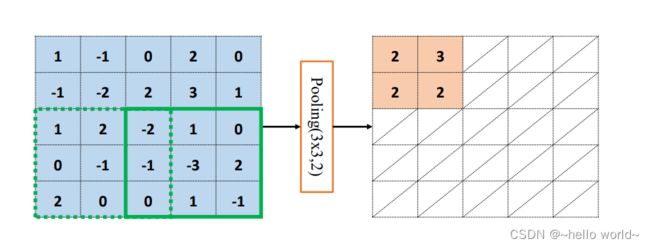
通过精心设计池化层感受野的高宽 和步长 参数,可以实现各种降维运算。比如,一种常用的池化层设定是感受野大小 =2,步长 =2,这样可以实现输出只有输入高宽一半的目的。如下图,感受野 =3,步长=2,输入 高宽为 4×4 ,输出高宽只有2 × 2。
![]()
6、BatchNorm 层
卷积神经网络的出现,网络参数量大大减低,使得几十层的深层网络成为可能,但网络的加深使得网络训练变得非常不稳定,甚至出现网络长时间不更新甚至不收敛的现象,同时网络对超参数比较敏感,超参数的微量扰动也会导致网络的训练轨迹完全改变。BN 层的提出,使得网络的超参数的设定更加自由,比如更大的学习率、更随意的网络初始化等,同时网络的收敛速度更快,性能也更好。
为什么需要对网络中的数据进行标准化操作?这个问题很难从理论层面解释透彻,与其纠结其缘由,不如通过具体问题来感受数据标准化后的好处。
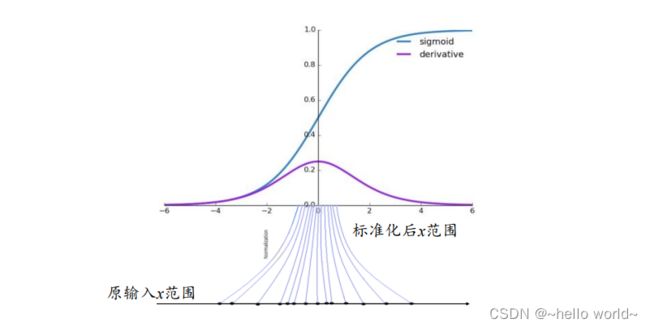
考虑 Sigmoid 激活函数和它的梯度分布。如下图, Sigmoid 函数在 ∈[−2,2] 区间的导数值在 [0.1,0.25] 区间分布;当 >2 或 <−2 时,Sigmoid 函数的导数变得很小,逼近于 0,从而容易出现梯度弥散现象。为了避免因为输入较大或者较小而导致 Sigmoid 函数出现梯度弥散现象,将函数输入 标准化映射到 0 附近的一段较小区间将变得非常重要,可以从图看到,通过标准化重映射后,值被映射在 0 附近,此处的导数值不至于过小,从而不容易出现梯度弥散现象。这是使用标准化手段受益的一个例子。
考虑 2 个输入节点的线性模型的具体例子:
ℒ = = 11 + 22 + b
讨论下列 2 种输入分布下的优化问题:
❑ 输入1 ∈[1,10] ,2 ∈ [1,10]
❑ 输入1 ∈[1,10] ,2 ∈ [100,1000]
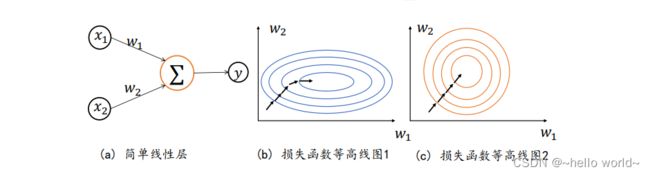
由于模型相对简单,可以绘制出 2 种 1、2 下,函数的损失等高线图,下图 b 是1 ∈[1,10] 、2 ∈[100,1000] 时的某条优化轨迹线示意,图 c 是1 ∈[1,10] 、2 ∈[1,10] 时的某条优化轨迹线示意,图中的圆环中心即为全局极值点。
由于
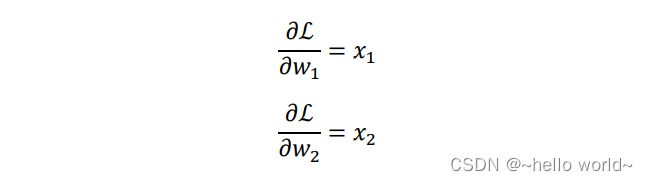
可知,当 1、2 输入分布相近时,两偏导数值相当,函数的优化轨迹如图 c 所示;当 1、2 输入分布差距较大时,比如1 ≪ 2,则两偏导数值相差较大,损失函数等势线在 2 轴更加陡峭,某条可能的优化轨迹如图 b 所示。对比 2 条优化轨迹线可以观察到,1、2 分布相近时图 c 中收敛更加快速,优化轨迹更理想。
通过上述的 2 个例子,可以归纳出:网络层输入 分布相近,并且分布在较小范围内时(如 0 附近),更有利于函数的优化。而数据标准化可以保证输入 的分布相近,将数据 映射到 ̂ :
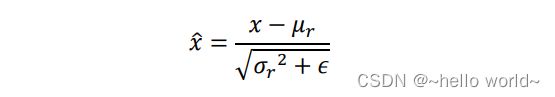
其中 、 2来自统计的所有数据的均值和方差, 是为防止出现除 0 而设置的较小数字,如 e−8。在基于 Batch 的训练阶段,如何获取每个网络层所有输入的统计数据 、2 呢?考虑 Batch 内部的均值 和方差 2:
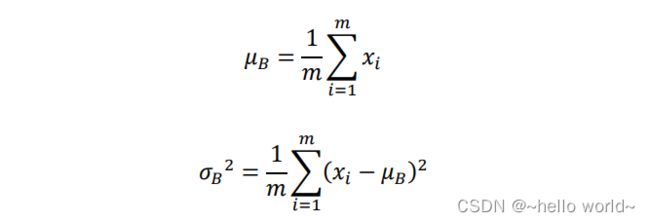
可以视为近似于、2,其中为 Batch 样本数。因此,在训练阶段,通过
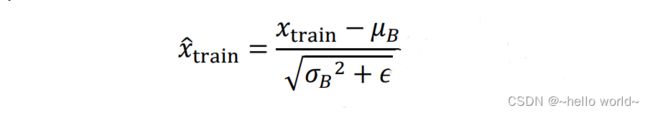
标准化输入,并记录每个 Batch 的统计数据 、2,用于统计真实的全局 、2。在测试阶段,根据记录的每个 Batch 的 、2 估计出所有训练数据的 、2,按着上述公式将每层的输入标准化。
上述的标准化运算并没有引入额外的待优化变量,、2 和 、2 均由统计得到,不需要参与梯度更新。实际上,为了提高 BN 层的表达能力,BN 层引入了 “scale and shift” 技巧,将 ̂ 变量再次映射变换:
![]()
其中 参数实现对标准化后的 ̂ 再次进行缩放, 参数实现对标准化的 ̂ 进行平移,不同的是,、 参数均由反向传播算法自动优化,实现网络层 “按需” 缩放平移数据的分布的目的。
6.1 BN 层的实现
6.1.1 前向传播
将 BN 层的输入记为 ,输出记为 ̃。分训练阶段和测试阶段来讨论前向传播过程。
训练阶段:首先计算当前 Batch 的 、2,根据公式计算 BN 层的输出。
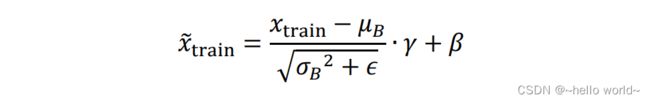
同时按照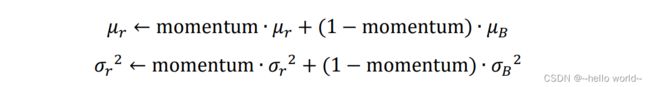
迭代更新全局训练数据的统计值 和 2 ,其中 momentum 是需要设置一个超参数,用于平衡 、2 的更新幅度。当 momentum = 0 时, 和 2 直接被设置为最新一个 Batch 的 和 2 ;当momentum = 1 时, 和 2 保持不变,忽略最新一个 Batch 的 和 2,在 TensorFlow 中,momentum 默认设置为 0.99。
测试阶段:BN 层根据公式
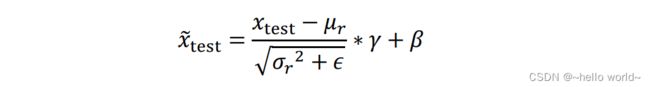
计算输出 ̃,其中 、2 、、 均来自训练阶段统计或优化的结果,在测试阶段直接使用,并不会更新这些参数。
6.1.2 反向更新
在训练模式下的反向更新阶段,反向传播算法根据损失 ℒ 求解梯度 ℒ/ 和 ℒ/,并按着梯度更新法则自动优化 、 参数。
需要注意的是,对于 2D 特征图输入: [b ℎ ] ,BN 层并不是计算每个点的 、2,而是在通道轴 上面统计每个通道上面所有数据的 、2,因此 、2 是每个通道上所有其它维度的均值和方差。以 shape 为 [100 32 32 3] 的输入为例,在通道轴 上面的均值计算,数据有 个通道数,则有 个均值产生,如下:
# 构造输入
x=tf.random.normal([100,32,32,3])
# 将其他维度合并,仅保留通道维度
x=tf.reshape(x,[-1,3])
# 计算其他维度的均值
ub=tf.reduce_mean(x,axis=0)
print(ub)
tf.Tensor([-0.0002406 0.0025879 0.00141215], shape=(3,), dtype=float32)
.
除了在轴上面统计数据 、2 的方式,很容易将其推广至其它维度计算均值的方式,如图所示:
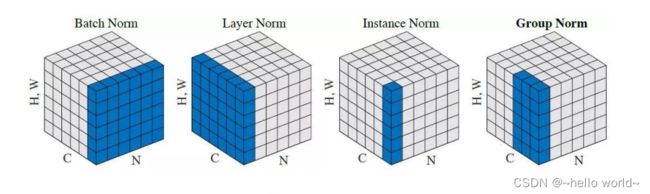
Layer Norm:统计每个样本的所有特征的均值和方差
Instance Norm:统计每个样本的每个通道上特征的均值和方差
Group Norm:将 通道分成若干组,统计每个样本的通道组内的特征均值和方差
6.1.3 BN 层实现
在 TensorFlow 中,通过 layers.BatchNormalization()类可以非常方便地实现 BN 层。与全连接层、卷积层不同,BN 层的训练阶段和测试阶段的行为不同,需要通过设置training 标志位来区分训练模式还是测试模式。在训练阶段,需要设置网络的参数 training=True 以区分 BN 层是训练还是测试模型;在测试阶段,需要设置 training=False,避免 BN 层采用错误的行为。
以 LeNet-5 的网络模型为例,在卷积层后添加 BN 层,代码如下:
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers, optimizers, Sequential, losses # 数据集, 网络层, 分类器, 容器
# 预处理 将浮点张量 x 限制在[-1,1]的范围内
def preprocess(x, y):
# x :[-1,1]
x = 2 * tf.cast(x, dtype=tf.float32) / 255 - 1
y = tf.cast(y, dtype=tf.int32)
return x, y
# 加载数据集
(x, y), (x_text, y_text) = datasets.mnist.load_data()
# 创建batch
train_db = tf.data.Dataset.from_tensor_slices((x, y))
train_db = train_db.map(preprocess).shuffle(1000).batch(128)
test_db = tf.data.Dataset.from_tensor_slices((x, y))
test_db = test_db.map(preprocess).batch(128)
# 通过 Sequential 容器创建 LeNet-5
network = Sequential([# 网络容器
layers.Conv2D(6,kernel_size=3,strides=1), # 第一个卷积层, 6 个 3x3 卷积核
# 插入 BN 层
layers.BatchNormalization(),
layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
layers.ReLU(), # 激活函数
layers.Conv2D(16,kernel_size=3,strides=1), # 第二个卷积层, 16 个 3x3 卷积核
# 插入 BN 层
layers.BatchNormalization(),
layers.MaxPooling2D(pool_size=2,strides=2), # 高宽各减半的池化层
layers.ReLU(), # 激活函数
layers.Flatten(), # 打平层,方便全连接层处理
layers.Dense(120, activation='relu'), # 全连接层,120 个节点
# 插入 BN 层
layers.BatchNormalization(),
layers.Dense(84, activation='relu'), # 全连接层,84 节点
# 插入 BN 层
layers.BatchNormalization(),
layers.Dense(10) # 全连接层,10 个节点
])
# build 一次网络模型,给输入 X 的形状,其中 4 为随意给的 batchsz
network.build(input_shape=(4, 28, 28, 1))
# 统计网络信息
network.summary()
# 创建损失函数类
criteon = losses.CategoricalCrossentropy(from_logits=True)
# w = w - lr * grad
# 学习率的设置,更新参数
optimizers = optimizers.Adam(learning_rate=1e-3)
# 模型训练
for epoch in range(5):
for step, (x, y) in enumerate(train_db):
with tf.GradientTape() as tape:
# 插入通道维度 =>[b,28,28,1]
x = tf.expand_dims(x, axis=3)
# 向前计算,获得10类的概率分布,[b,784]-> [b,10]
out = network(x,training=True)
# 真实标签 one-hot 编码, [b] => [b, 10]
y_onehot = tf.one_hot(y, depth=10)
# 计算交叉熵损失函数,标量
loss = criteon(y_onehot, out)
# 自动计算梯度
grads = tape.gradient(loss, network.trainable_variables)
# 自动跟新参数
optimizers.apply_gradients(zip(grads, network.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'loss', float(loss))
# 测试集,记录预测正确的数量,总样本数量
total_correct, total = 0, 0
for x, y in test_db:
# 插入通道维数
x = tf.expand_dims(x, axis=3)
# 前向计算,获得 10 类别的预测分布, [b, 784] => [b, 10]
out = network(x,training=False)
# 将输出结果归一化处理,得到和为1的概率
prob = tf.nn.softmax(out, axis=1) # [0,1]
# 找到对应维度最大值的索引位置
pred = tf.argmax(prob, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# pred:[b]
# y: [b]
# correct: [b], True(1): equal; False(0): not equal
correct = tf.equal(pred, y)
correct = tf.reduce_sum(tf.cast(correct, dtype=tf.int32))
# 预测对的数量
total_correct += int(correct)
# 统计预测样本总数
total += x.shape[0]
# acc
print('acc:', total_correct / total)
7、卷积层变种
7.1 空洞卷积
普通的卷积层为了减少网络的参数量,卷积核的设计通常选择较小的 1×1 和 3×3 感受野大小。小卷积核使得网络提取特征时的感受野区域有限,但是增大感受野的区域又会增加网络的参数量和计算代价,因此需要权衡设计。
空洞卷积(Dilated/Atrous Convolution)的提出较好地解决这个问题,空洞卷积在普通卷积的感受野上增加一个 Dilation Rate 参数,用于控制感受野区域的采样步长,如下图:
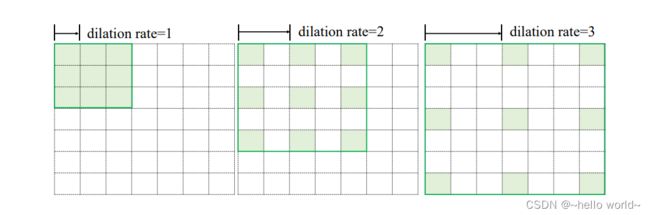
当感受野的采样步长 Dilation Rate 为 1 时,每个感受野采样点之间的距离为 1,此时的空洞卷积退化为普通的卷积;当 Dilation Rate 为 2 时,感受野每 2 个单元采样一个点,上图中间的绿色方框中绿色格子所示,每个采样格子之间的距离为 2;当 Dilation Rate 为 3,采样步长为 3。尽管 Dilation Rate 的增大会使得感受野区域增大,但是实际参与运算的点数仍然保持不变。
空洞卷积在不增加网络参数的条件下,提供了更大的感受野窗口。但是在使用空洞卷积设置网络模型时,需要精心设计 Dilation Rate 参数来避免出现网格效应,同时较大的Dilation Rate 参数并不利于小物体的检测、语义分割等任务。
在 TensorFlow 中,可以通过设置 layers.Conv2D()类的 dilation_rate 参数来选择使用普通卷积还是空洞。当 dilation_rate 参数设置为默认值 1 时,使用普通卷积方式进行运算;当 dilation_rate 参数大于 1 时,采样空洞卷积方式进行计算。
layer = layers.Conv2D(1,kernel_size=3,strides=1,dilation_rate=2)
.
7.2 转置卷积
转置卷积(Transposed Convolution) 通过在输入之间填充大量的 padding 来实现输出高宽大于输入高宽的效果,从而实现向上采样的目的,如图所示:
为了简化讨论,此处只讨论输入 ℎ=,即输入高宽相等的情况,介绍转置卷积的计算过程。
+ − 为 倍数
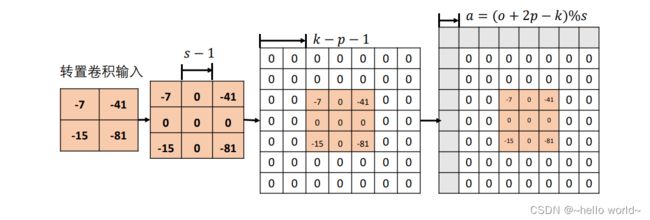
考虑输入为 2×2 的单通道特征图,转置卷积核为3×3 大小,步长 =2,填充 =0 的例子。首先在输入数据点之间均匀插入 −1 个空白数据点,得到 3×3 的矩阵,根据填充量在 3×3 矩阵周围填充相应 −−1= 3−0−1=2 行/列,此时输入张量的高宽为 7×7,如图所示:
在 7×7 的输入张量上,进行 3×3 卷积核,步长 ′ =1 ,填充 =0 的普通卷积运算(注意,此阶段的普通卷积的步长 ′ 始终为 1,与转置卷积的步长 不同),根据普通卷积的输出计算公式,得到输出大小为:
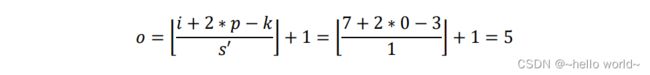
5×5 大小的输出。直接按照此计算流程给出最终转置卷积输出与输入关系,即在 +2−为 s 倍数时,满足关系:
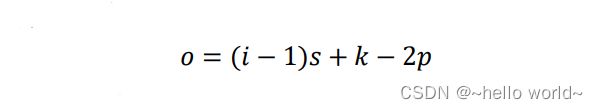
转置卷积鱼普通卷积的逆过程的联系:在相同的设定下,输入 经过普通卷积运算后得到 = Conv(),将 送入转置卷积运算后,得到 ′ = ConvTranspose(),其中 ′ ≠ ,但是 ′ 与 形状相同。以输入为 5×5,步长 =2,填充 =0,3×3 卷积核的普通卷积运算进行验证演示,如下图所示:
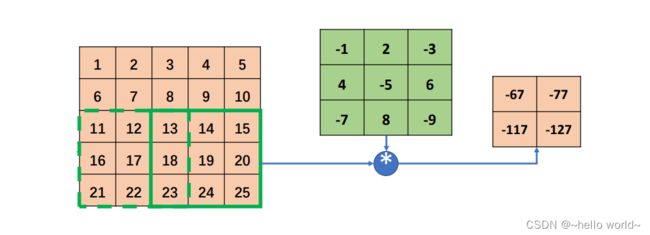
代码实现:
# 创建 X 矩阵,高宽为 5x5
x = tf.range(25)+1
# Reshape 为合法维度的张量
x = tf.reshape(x,[1,5,5,1])
x = tf.cast(x, tf.float32)
# 创建固定内容的卷积核矩阵
w = tf.constant([[-1,2,-3.],[4,-5,6],[-7,8,-9]])
# 调整为合法维度的张量
w = tf.expand_dims(w,axis=2)
w = tf.expand_dims(w,axis=3)
# 进行普通卷积运算
out = tf.nn.conv2d(x,w,strides=2,padding='VALID')
print('普通卷积运算\n',out)
print('----------------------')
# 普通卷积的输出作为转置卷积的输入,进行转置卷积运算
xx = tf.nn.conv2d_transpose(out, w, strides=2,padding='VALID',output_shape=[1,5,5,1])
print('将 送入转置卷积运算\n',xx)

可以看到,转置卷积能够恢复出同大小的普通卷积的输入,但转置卷积的输出并不等同于普通卷积的输入。
.
+ − 不为倍数
首先,让我们更加深入地分析卷积运算中输入与输出大小关系的一个细节。考虑卷积运算的输出表达式:
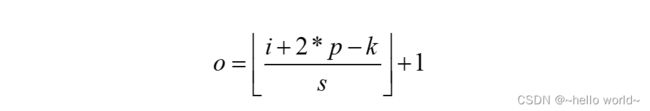
当步长 s>1 时,分数项向下取整运算使得出现多种不同输入尺寸 对应到相同的输出尺寸 上。
矩阵角度理解转置卷积
转置卷积的转置是指卷积核矩阵 产生的稀疏矩阵 ′ 在计算过程中需要先转置 ′,再进行矩阵相乘运算,而普通卷积并没有转置 ′ 的步骤。
考虑普通 Conv2d 运算: 和 ,需要根据 strides 将卷积核在行、列方向循环移动获取参与运算的感受野的数据,串行计算每个窗口处的 “相乘累加” 值,计算效率极低。为了加速运算,在数学上可以将卷积核 根据 strides 重排成稀疏矩阵 ′,再通过 ′@′ 一次完成运算(实际上,′矩阵过于稀疏,导致很多无用的 0 乘运算)。以 4 行 4 列的输入 ,高宽为 3×3,步长为 1,无 padding 的卷积核 的卷积运算为例,首先将 打平成 ′,如图 所示:
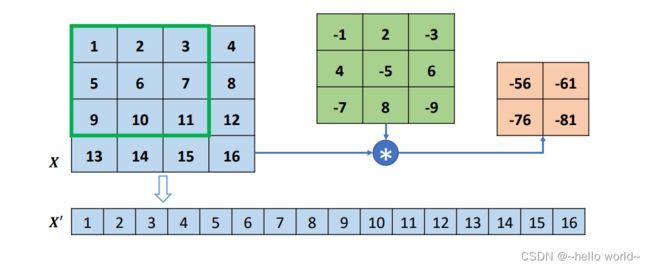
然后将卷积核转换成稀疏矩阵′,如下图:
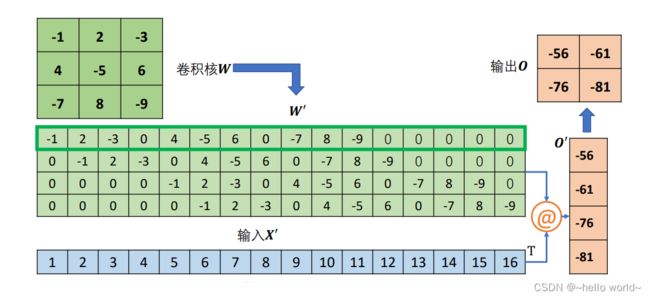
此时通过一次矩阵相乘即可实现普通卷积运算:′ = ′@′
.
如果给定 ,怎么生成与同形状大小的张量呢?将 ′ 转置后与第一步重排后的 ′ 完成矩阵相乘即可:′ = ′ T@′ 得到的 ′ 通过 Reshape 操作变为与原来的输入尺寸一致,但是内容不同。由于转置卷积在矩阵运算时,需要将′转置后才能与转置卷积的输入 ′ 矩阵相乘,故称为转置卷积。
转置卷积实现
在 TensorFlow 中,可以通过 nn.conv2d_transpose 实现转置卷积运算。我们先通过nn.conv2d 完成普通卷积运算。注意转置卷积的卷积核的定义格式为 [ ] 。在使用 tf.nn.conv2d_transpose 进行转置卷积运算时,需要额外手动设置输出的高宽。tf.nn.conv2d_transpose 并不支持自定义 padding 设置,只能设置为 VALID 或者 SAME。
# 创建 4x4 大小的输入
x = tf.range(16)+1
x = tf.reshape(x,[1,4,4,1])
x = tf.cast(x, tf.float32)
# 创建 3x3 卷积核
w = tf.constant([[-1,2,-3.],[4,-5,6],[-7,8,-9]])
w = tf.expand_dims(w,axis=2)
w = tf.expand_dims(w,axis=3)
# 普通卷积运算
out = tf.nn.conv2d(x,w,strides=1,padding='VALID')
# 创建转置卷积类
layer = layers.Conv2DTranspose(1,kernel_size=3,strides=1,padding='VALID')
xx2 = layer(out) # 通过转置卷积层
xx2
7.3 分离卷积
以深度可分离卷积(Depth-wise Separable Convolution)为例。普通卷积在对多通道输入进行运算时,卷积核的每个通道与输入的每个通道分别进行卷积运算,得到多通道的特征图,再对应元素相加产生单个卷积核的最终输出,如下图所示:
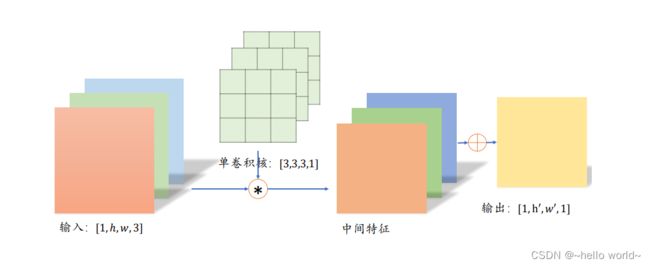
.
分离卷积的计算流程则不同,卷积核的每个通道与输入的每个通道进行卷积运算,得到多个通道的中间特征。多通道的中间特征张量接下来进行多个 1×1 卷积核的普通卷积运算,得到多个高宽不变的输出,这些输出在通道轴上面进行拼接,从而产生最终的分离卷积层的输出。可以看到,分离卷积层包含了两步卷积运算,第一步卷积运算是单个卷积核,第二个卷积运算包含了多个卷积核。如下图所示:
![]()
分离卷积的优势在于,同样的输入和输出,采用
Separable Convolution 的参数量约是普通卷积的 1 3 \frac{1}{3} 31。考虑上图中的普通卷积和分离卷积的例子普通卷积的参数量是
3 × 3 × 3 × 4 = 108 3 × 3 ×3×4= 108 3×3×3×4=108
分离卷积的第一部分参数量是
3 × 3 × 3 × 1 = 27 3 × 3 ×3×1= 27 3×3×3×1=27
第二部分参数量是
1 × 1 × 3 × 4 = 12 1 × 1 ×3×4= 12 1×1×3×4=12
分离卷积的总参数量只有39,但是却能实现普通卷积同样的输入输出尺寸变换。分离卷积在 Xception 和 MobileNets 等对计算代价敏感的领域中得到了大量应用。
8、深度残差网络
当模型加深以后,网络变得越来越难训练,这主要是由于梯度弥散和梯度爆炸现象造成的。在较深层数的神经网络中,梯度信息由网络的末层逐层传向网络的首层时,传递的过程中会出现梯度接近于 0 或梯度值非常大的现象。网络层数越深,这种现象可能会越严重。通过在输入和输出之间添加一条直接连接的 Skip Connection 可以让神经网络具有回退的能力。
以 VGG13 深度神经网络为例,假设观察到 VGG13 模型出现梯度弥散现象,而10 层的网络模型并没有观测到梯度弥散现象,那么可以考虑在最后的两个卷积层添加 Skip Connection,通过这种方式,网络模型可以自动选择是否经由这两个卷积层完成特征变换,还是直接跳过这两个卷积层而选择 Skip Connection,亦或结合两个卷积层和 Skip Connection 的输出。如下图所示:
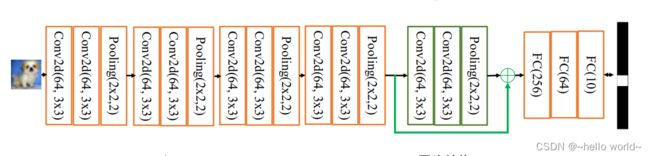
8.1 ResNet 原理
2015 年,何凯明等人发表了基于 Skip Connection 的深度残差网络(Residual Neural Network,简称 ResNet)算法。
ResNet 通过在卷积层的输入和输出之间添加 Skip Connection 实现层数回退机制。输入 通过两个卷积层,得到特征变换后的输出 ℱ(),与输入进行对应元素的相加运算,得到最终输出 ℋ():
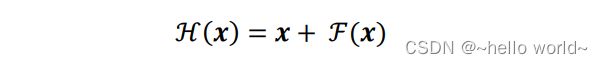
ℋ()叫作残差模块(Residual Block,简称 ResBlock)。由于被 Skip Connection 包围的卷积神经网络需要学习映射ℱ() = ℋ() − ,故称为残差网络。
为了能够满足输入与卷积层的输出ℱ()能够相加运算,需要输入的 shape 与ℱ()的 shape 完全一致。当出现 shape 不一致时,一般通过在 Skip Connection 上添加额外的卷积运算环节将输入变换到与ℱ()相同的 shape,如下图中 identity() 函数所示,其中 identity() 以 1×1 的卷积运算居多,主要用于调整输入的通道数。
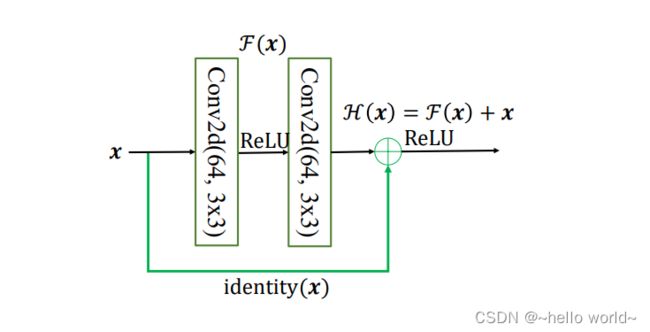
8.2 ResBlock 实现
深度残差网络并没有增加新的网络层类型,只是通过在输入和输出之间添加一条 Skip Connection,因此并没有针对 ResNet 的底层实现。在 TensorFlow 中通过调用普通卷积层即可实现残差模块。
首先创建一个新类,在初始化阶段创建残差块中需要的卷积层、激活函数层等,首先新建ℱ()卷积层,代码如下:
class BasicBlock(layers.Layer):
# 残差模块类
def __init__(self, filter_num, stride=1):
super(BasicBlock, self).__init__()
# f(x)包含了 2 个普通卷积层,创建卷积层 1
self.conv1 = layers.Conv2D(filter_num, (3, 3), strides=stride, padding='same')
self.bn1 = layers.BatchNormalization()
self.relu = layers.Activation('relu')
# 创建卷积层 2
self.conv2 = layers.Conv2D(filter_num, (3, 3), strides=1, padding='same')
self.bn2 = layers.BatchNormalization()
# 当ℱ()的形状与不同时,无法直接相加,需要新建identity()卷积层,来完成的形状转换。
if stride != 1: # 插入 identity 层
self.downsample = Sequential()
self.downsample.add(layers.Conv2D(filter_num, (1, 1), strides=stride))
else: # 否则,直接连接
self.downsample = lambda x:x
# 在前向传播时,只需要将ℱ()与identity()相加,并添加 ReLU 激活函数即可
def call(self, inputs, training=None):# 前向传播函数
out = self.conv1(inputs) # 通过第一个卷积层
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out) # 通过第二个卷积层
out = self.bn2(out)
# 输入通过 identity()转换
identity = self.downsample(inputs)
# f(x)+x 运算
output = layers.add([out, identity])
# 再通过激活函数并返回
output = tf.nn.relu(output)
return output