基于Graph的Embedding方法概述
原文链接:基于 Graph 的 Embedding 方法概述
文章目录
- Graph Embedding
-
- 浅层图模型
-
- DeepWalk
- Node2vec
- Metapath2vec
- 深度图模型
-
- GCN
- GraphSAGE
- 总结
Graph Embedding
基于内容的Embedding方法(如word2vec、BERT等)都是针对“序列”样本(如句子、用户行为序列)设计的,但在互联网场景下,数据对象之间更多呈现出图结构,如下图所示 (1) 有用户行为数据生成的物品关系图;(2) 有属性和实体组成的只是图谱。
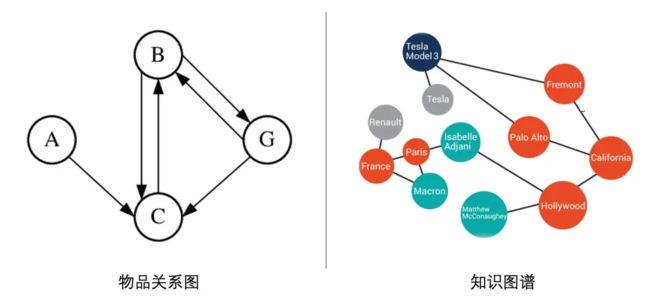
对于图结构数据,基于内容的embedding方法不太好直接处理了。因此,为了解决图结构数据的问题,Graph Embedding开始得到大家的重视,并在各个领域进行尝试;
Graph Embedding是一种将图结构数据映射为低微稠密向量的过程,从而捕捉到图的拓扑结构、顶点与顶点的关系、以及其他的信息。目前,Graph Embedding方法大致可以分为两大类:
- 浅层图模型;
- 深度图模型。
浅层图模型
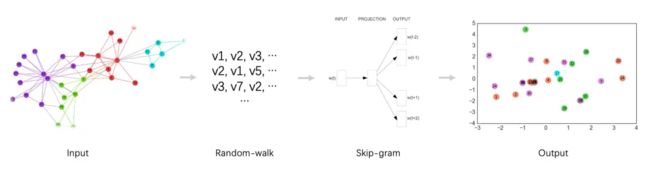
浅层图模型主要是采用random-walk + skip-gram模式的embedding方法。主要是通过在图中采用随机游走策略来生成多条节点列表,然后将每个列表相当于含有多个单词(图中的节点)的句子,再用skip-gram模型来训练每个节点的向量。这些方法主要包括DeepWalk、Node2vec、Metapath2vec等。
DeepWalk
DeepWalk是第一个将NLP中的思想用在Graph Embedding上的算法,输入是一张图,输出是网络中节点的向量表示,使得图中两个点共有的邻居节点(或者高阶邻近点)越多,则对应的两个向量之间的距离就越近。
DeepWalk得本质可以认为是:random walk + skip-gram。在DeepWalk算法中,需要形式化定义的是random walk的跳转概率,即到达节点后,下一步遍历其邻居节点的概率:
P ( v j ∣ v i ) = { M i j ∑ k ∈ N + ( v i ) M i k , v j ∈ N + ( v i ) 0 , v j ∉ N + ( v i ) P\left(v_{j} \mid v_{i}\right)=\left\{\begin{array}{ll} \frac{M_{i j}}{\sum_{k \in N_+\left(v_{i}\right)} M_{i k}} & , v_{j} \in N_{+}\left(v_{i}\right) \\ 0 & , v_{j} \notin N_{+}\left(v_{i}\right) \end{array}\right. P(vj∣vi)={∑k∈N+(vi)MikMij0,vj∈N+(vi),vj∈/N+(vi)
其中, N + ( v i ) N_+\left(v_{i}\right) N+(vi) 表示节点的所有出边连接的节点集合, M i j M_{ij} Mij表示由节点 i i i 连接至节点 j j j 的边的权重。由此可见,原始DeepWalk算法的跳转概率是跳转边的权重占所有相关出边权重之和的比例。算法具体步骤如下图所示:

DeepWalk算法原理简单,在网络标注顶点很少的情况也能得到比较好的效果,且具有较好的可扩展性,能够适应网络的变化。但由于DeepWalk采用的游走策略过于简单(BFS),无法有效表征图的节点的结构信息。
Node2vec
为了克服DeepWalk模型的random walk策略相对简单的问题,斯坦福大学的研究人员在2016年提出了Node2vec模型。该模型通过调整random walk权重的方法使得节点的embedding向量更倾向于体现网络的同质性或结构性。
-
同质性:指得是距离相近的节点的embedding向量应近似,如下图中,与节点 u u u 相连的节点 s 1 , s 2 , s 3 , s 4 s_1, s_2, s_3, s_4 s1,s2,s3,s4的embedding向量应相似。为了使embedding向量能够表达网络的同质性,需要让随机游走更倾向于DFS,因为DFS更有可能通过多次跳转,到达远方的节点上,使游走序列集中在一个较大的集合内部,使得在一个集合内部的节点具有更高的相似性,从而表达图的同质性。
-
结构性:结构相似的节点的embedding向量应近似,如下图中,与节点 u u u 结构相似的节点 s 6 s_6 s6 的embedding向量应相似。为了表达结构性,需要随机游走更倾向于BFS,因为BFS会更多的在当前节点的邻域中游走,相当于对当前节点的网络结构进行扫描,从而使得embedding向量能刻画节点邻域的结构信息。
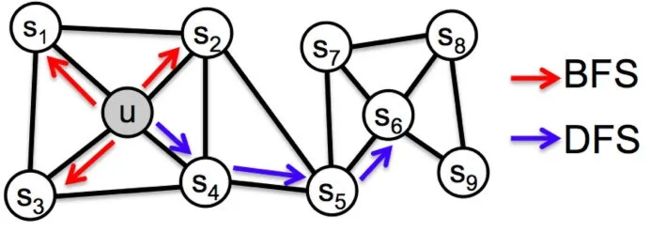
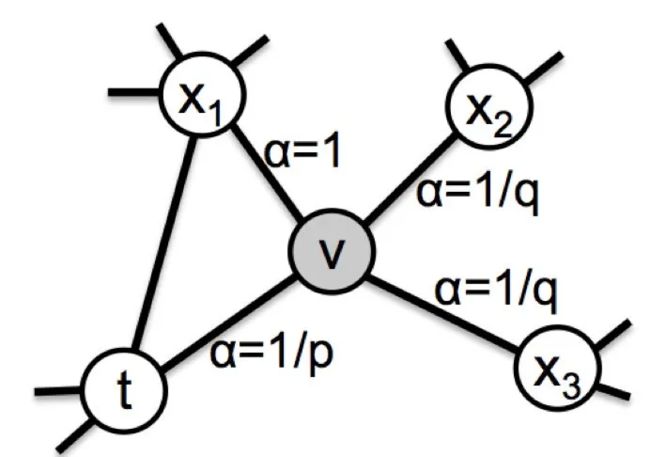
在Node2vec中,同样是通过控制节点间的跳转概率来控制BFS和DFS倾向性的。如下图所示,当算法先由节点 t t t 跳转到节点 v v v,准备从节点 v v v 跳转至下一个节点时,各节点概率定义如下:
π v x = α p , q ( t , x ) ⋅ w v x \pi_{v x}=\alpha_{p, q}(t, x) \cdot w_{v x} πvx=αp,q(t,x)⋅wvx
其中, w v x w_{vx} wvx是节点和边的权重, α p , q ( t , x ) \alpha_{p, q}(t, x) αp,q(t,x) 定义如下:
α ( t , x ) = { 1 p if d t x = 0 1 if d t x = 1 1 q if d t x = 2 \alpha(t, x)=\left\{\begin{array}{ll} \frac{1}{p} & \text { if } d_{t x}=0 \\ 1 & \text { if } d_{t x}=1 \\ \frac{1}{q} & \text { if } d_{t x}=2 \end{array}\right. α(t,x)=⎩⎨⎧p11q1 if dtx=0 if dtx=1 if dtx=2
d t x d_{tx} dtx表示节点 t t t 与 x x x 的最短路径,如 t t t 与 x 1 x_1 x1 的最短路径为1。作者引入了两个参数和来控制游走算法的BFS和DFS倾向性:
- return parameter p p p:值越小,随机游走回到节点的概率越大,最终算法更注重表达网络的结构性
- In-out parameter q q q:值越小,随机游走到远方节点的概率越大,算法更注重表达网络的同质性
当 p = q = 1 p=q=1 p=q=1 时,Node2vec退化成了DeepWalk算法。
下图是作者通过调整 p p p 和 q q q,使embedding向量更倾向于表达同质性和结构性的可视化结果:
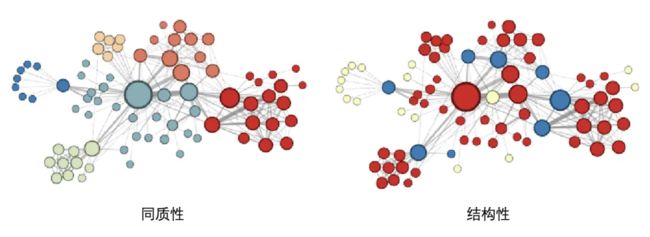
从图中可以看出,同质性倾向使相邻的节点相似性更高,而结构性相似使得结构相似的节点具有更高的相似性。Node2vec的算法步骤如下:

相较于DeepWalk,Node2vec通过设计biased-random walk策略,能对图中节点的结构相似性和同质性进行权衡,使模型更加灵活。但与DeepWalk一样,Node2vec无法指定游走路径,且仅适用于解决只包含一种类型节点的同构网络,无法有效表示包含多种类型节点和边类型的复杂网络。
Metapath2vec
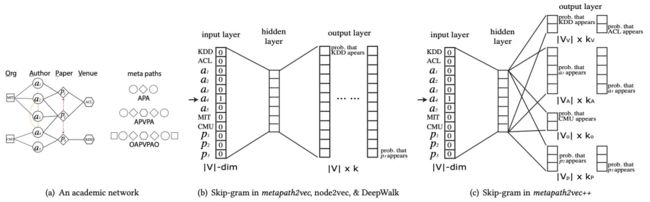
为了解决Node2vec和DeepWalk无法指定游走路径、处理异构网络的问题,Yuxiao Dong等人在2017年提出了Metapath2vec方法,用于对异构信息网络(Heterogeneous Information Network, HIN)的节点进行embedding。
Metapath2vec总体思想跟Node2vec和DeepWalk相似,主要是在随机游走上使用基于meta-path的random walk来构建节点序列,然后用Skip-gram模型来完成顶点的Embedding。
异构网络(Heterogeneous Network)的定义如下:
异构网络 G ( V , E , T ) G(V, E, T) G(V,E,T) 其中节点和边的映射函数为 ϕ ( v ) : v → T v 和 φ ( e ) \phi(v): v \rightarrow T_{v} \text { 和 } \varphi(e) ϕ(v):v→Tv 和 φ(e)。即,存在多种类型节点或边的网络为异构网络。
虽然节点类型不同,但是不同类型的节点会映射到同一个特征空间。由于异构性的存在,传统的基于同构网络的节点向量化方法很难有效地直接应用在异构网络上。
为了解决这个问题,作者提出了meta-path-based random walk:通过不同meta-path scheme 来捕获不同类型节点之间语义和结构关系。meta-path scheme定义如下:
V 1 → R 1 V 2 → R 2 … V t → R t V t + 1 … V l − 1 → R l 1 V l V_{1} \stackrel{R_{1}}{\rightarrow} V_{2} \stackrel{R_{2}}{\rightarrow} \ldots V_{t} \stackrel{R_{t}}{\rightarrow} V_{t+1} \ldots V_{l-1} \stackrel{R_{l}}{\rightarrow}^{1} V_{l} V1→R1V2→R2…Vt→RtVt+1…Vl−1→Rl1Vl
其中 R t R_t Rt 表示不同类型节点 V t V_t Vt 和 V t + 1 V_{t+1} Vt+1 之间的关系。节点的跳转概率为:
p ( v i + 1 ∣ v t i , P ) = { 1 ∣ N t + 1 ( v t v ) ∣ if ( v i + 1 , v t i ) ∈ E & ϕ ( v i + 1 ) = t + 1 0 if ( v i + 1 , v t i ) ∈ E & ϕ ( v i + 1 ) ≠ t + 1 0 i f ( v i + 1 , v t i ) ∉ E p\left(v^{i+1} \mid v_{t}^{i}, P\right)=\left\{\begin{array}{rr} \frac{1}{\left|N_{t+1}\left(v_{t}^{v}\right)\right|} & \text { if }\left(v^{i+1}, v_{t}^{i}\right) \in E \& \phi\left(v^{i+1}\right)=t+1 \\ 0 & \text { if }\left(v^{i+1}, v_{t}^{i}\right) \in E \& \phi\left(v^{i+1}\right) \neq t+1 \\ 0 & i f\left(v^{i+1}, v_{t}^{i}\right) \notin E \end{array}\right. p(vi+1∣vti,P)=⎩⎨⎧∣Nt+1(vtv)∣100 if (vi+1,vti)∈E&ϕ(vi+1)=t+1 if (vi+1,vti)∈E&ϕ(vi+1)=t+1if(vi+1,vti)∈/E
其中, v t i ∈ V t v_t^i\in V_t vti∈Vt, N t + 1 ( v t i ) N_{t+1}(v_t^i) Nt+1(vti)表示节点 v t i v_t^i vti的 V t + 1 V_{t+1} Vt+1 类型的邻居节点集合。meta-path的定义一般是对称的,比如 user-item-tag-item-user。最后采用skip-gram来训练节点的embedding向量:
O = arg max θ ∑ v ∈ V ∑ t ∈ T v ∑ c t ∈ N t ( v ) log p ( c t ∣ v ; θ ) O=\underset{\theta}{\arg \max } \sum_{v \in V} \sum_{t \in T_{v}} \sum_{c_{t} \in N_{t}(v)} \log p\left(c_{t} \mid v ; \theta\right) O=θargmaxv∈V∑t∈Tv∑ct∈Nt(v)∑logp(ct∣v;θ)
其中: N t ( v ) N_t(v) Nt(v) 表示节点的上下文中,类型为 t t t 的节点,
p metapath 2 v e c ( c t ∣ v ; θ ) = e X c t ⋅ X v ∑ u ∈ V e X u ⋅ X v p_{\text {metapath} 2 v e c}\left(c_{t} \mid v ; \theta\right)=\frac{e^{X_{c_{t}} \cdot X_{v}}}{\sum_{u \in V} e^{X_{u} \cdot X_{v}}} pmetapath2vec(ct∣v;θ)=∑u∈VeXu⋅XveXct⋅Xv
通过分析metapath2vec目标函数可以发现,该算法仅在游走是考虑了节点的异构性,但在skip-gram训练时却忽略了节点的类型。为此,作者进一步提出了metapath2vec++算法,在skip-gram模型训练时将同类型的节点进行softmax归一化:
p metapath 2 v e c + + ( c t ∣ v ; θ ) = e X c t ⋅ X v ∑ u t ∈ V t e X u t ⋅ X v p_{\text {metapath} 2 v e c++}\left(c_{t} \mid v ; \theta\right)=\frac{e^{X_{c_{t}} \cdot X_{v}}}{\sum_{u_{t} \in V_{t}} e^{X_{u_{t}} \cdot X_{v}}} pmetapath2vec++(ct∣v;θ)=∑ut∈VteXut⋅XveXct⋅Xv
metaptah2vec和metapath2vec++的skip-gram模型结构如下图所示:
深度图模型
上一节讲的浅层图模型方法在世纪应用中是先根据图的结构学习每个节点的embedding向量,然后再讲得到的embedding向量应用于下游任务重。然而,embedding向量和下游任务是分开学习的,也就是说学得的embedding向量针对下游任务来说不一定是最优的。为了解决这个embedding向量与下游任务的gap,研究人员尝试讲深度图模型是指将图与深度模型结合,实现end-to-end训练模型,从而在图中提取拓扑图的空间特征。主要分为四大类:
- Graph Convolution Networks (GCN)
- Graph Attention Networks (GAT)
- Graph AutoEncoder (GAE)
- Graph Generative Networks (GGN)
本节主要简单介绍GCN中的两个经典算法:1)基于谱的GCN (GCN);2)基于空间的GCN (GraphSAGE)。
提取拓扑图的空间特征的方法主要分为两大类:1)基于空间域或顶点域spatial domain(vertex domain)的;2)基于频域或谱域spectral domain的。通俗点解释,空域可以类比到直接在图片的像素点上进行卷积,而频域可以类比到对图片进行傅里叶变换后,再进行卷积。
- 基于spatial domain:基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上,跟传统的卷积神经网络中的卷积更相似一些。主要有两个问题:1)按照什么条件去找中心节点的邻居,也就是如何确定receptive field;2)按照什么方式处理包含不同数目邻居的特征。
- 基于spectral domain:借助卷积定理可以通过定义频谱域上的内积操作来得到空间域图上的卷积操作。
GCN
理论参考以下文章:
- 图卷积网络GCN(Graph Convolution Network)(一)研究背景和空域图卷积
- 图卷积网络GCN(Graph Convolution Network)(二)图上的傅里叶变换和逆变换
- 图卷积网络GCN(Graph Convolution Network)(三)详解三代图卷积网络理论
GraphSAGE
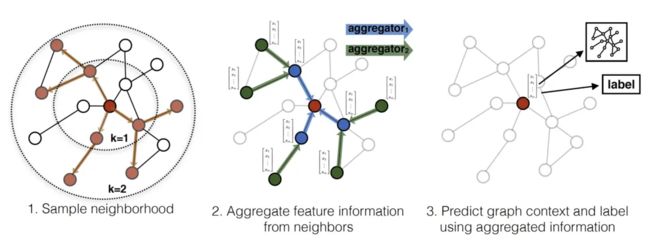
GraphSAGE(Graph SAmple and aggreGatE)是基于空间域方法,其思想与基于频谱域方法相反,是直接在图上定义卷积操作,对空间上相邻的节点上进行运算。其计算流程主要分为三步:
- 对图中每个节点领据节点进行采样
- 根据聚合函数聚合邻居节点信息(特征)
- 得到图中各节点的embedding向量,供下游任务使用
其中 K K K 表示每个节点能够聚合的邻居节点的跳数(例如 K = 2 K=2 K=2 时,每个顶点可以最多根据其2跳邻居节点的信息来表示自身的embedding向量)。算法直观上是在每次迭代中,节点聚合邻居信息。随着不断迭代,节点得到图中来自越来越远的节点信息。
邻居节点采样:在每个epoch中,均匀地选取固定大小的邻居数目,每次迭代选取不同的均匀样本。
GraphSAGE的损失函数如下:
J g ( z u ) = log ( σ ( z u T z v ) ) − Q ⋅ E v n ∼ P n ( v ) log ( σ ( − z u T z v n ) ) J_{g}\left(z_{u}\right)=\log \left(\sigma\left(z_{u}^{T} z_{v}\right)\right)-Q \cdot E_{v_{n} \sim P_{n}(v)} \log \left(\sigma\left(-z_{u}^{T} z_{v_{n}}\right)\right) Jg(zu)=log(σ(zuTzv))−Q⋅Evn∼Pn(v)log(σ(−zuTzvn))
其中, z u z_u zu和 z v z_v zv表示节点 u u u和 v v v的embedding向量, v v v是 u u u固定长度的邻居节点, σ \sigma σ 是sigmoid函数, P n P_n Pn和 Q Q Q分别表示负样本分布和数目。
对于聚合函数的,由于在图中节点的邻居是无序的,聚合函数应是对称的(改变输入节点的顺序,函数的输出结果不变),同时又具有较强的表示能力。主要有如下三大类的聚合函数:
- Mean aggretator:将目标节点和其邻居节点的第k-1层向量拼接起来,然后对计算向量的element-wise均值,最后通过对均值向量做非线性变换得到目标节点邻居信息表示:
h y k ← σ ( W ⋅ M E A N ( { h y k − 1 } ∪ { h u k − 1 , ∀ u ∈ N ( v ) } ) ) h_{y}^{k} \leftarrow \sigma\left(W \cdot M E A N\left(\left\{h_{y}^{k-1}\right\} \cup\left\{h_{u}^{k-1}, \forall u \in N(v)\right\}\right)\right) hyk←σ(W⋅MEAN({hyk−1}∪{huk−1,∀u∈N(v)})) - Pooling aggregator:先对目标节点的邻居节点向量做非线性变换并采用pooling操作(maxpooling或meanpooling)得到目标节点的邻居信息表示:
A G G R E G A T E k p o o l = max ( { σ ( W p o o l h u i k + b ) , ∀ u i ∈ N A G G R E G A T E_{k}^{p o o l}=\max \left(\left\{\sigma\left(W_{p o o l} h_{u_{i}}^{k}+b\right), \forall u_{i} \in N\right.\right. AGGREGATEkpool=max({σ(Wpoolhuik+b),∀ui∈N - LSTM aggretator:使用LSTM来encode邻居的特征,为了忽略邻居之间的顺序,需要将邻居节点顺序打乱之后输入到LSTM中。LSTM相比简单的求平均和Pooling操作具有更强的表达能力。
后续…
总结
在实际过程中,不同的向量化方法得到的embedding结果也会有较大差异,需要根据具体业务需求来选择相应的算法。如要挖掘用户与用户的同质性,可以尝试采用Node2vec;此外,如果需要结合物品或Item的side-info,可以考虑GraphSAGE算法来对图中节点进行embedding。