pytorch常用函数总结（更新中）

目录

一、 初始化张量

1. torch.arange()和range()

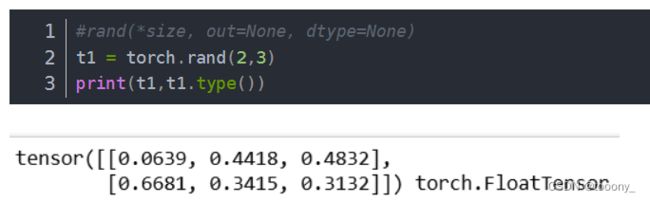
2. torch.rand()、torch.randn()、torch.randint()、torch.randperm()、torch.normal() 

 二、 运算

1.张量比较

2. torch.eq

3. torch.sum

4. torch.mean

5. torch.mm

6. torch.matmul

7. torch.clamp

8. torch.max

9. torch.norm

10. torch.argmax

三、维度操作

1. torch.cat

2. torch.chunk

3. torch.squeeze和unqueeze

---

一、 初始化张量

1. torch.arange()和range()

torch.arange(start=0, end, step=1, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor

    >>> torch.arange(5)  # 默认以 0 为起点
    tensor([ 0,  1,  2,  3,  4])
    >>> torch.arange(1, 4)  # 默认间隔为 1
    tensor([ 1,  2,  3])
    >>> torch.arange(1, 2.5, 0.5)  # 指定间隔 0.5
    tensor([ 1.0000,  1.5000,  2.0000])

torch.range(start=0, end, step=1, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensor

>>> y=torch.range(1,6)
>>> y
tensor([1., 2., 3., 4., 5., 6.])

2. torch.rand()、torch.randn()、torch.randint()、torch.randperm()、torch.normal() 

 

 torch.randint()同rand，生成int（均匀分布）

torch.randperm

torch.randperm(n, generator=None, out=None, dtype=torch.int64, layout=torch.strided, device=None, requires_grad=False, pin_memory=False) → Tensor

 torch.normal() 

返回一个张量，包含了从指定均值mean和标准差std的离散正态分布中抽取的一组随机数。

torch.normal(mean, std, generator=None, out=None) → Tensor

torch.normal(mean=torch.arange(1., 11.), std=torch.arange(1, 0, -0.1))
 
返回：
tensor([  1.0425,   3.5672,   2.7969,   4.2925,   4.7229,   6.2134,
          8.0505,   8.1408,   9.0563,  10.0566])

torch.normal(mean=torch.arange(1., 6.))
 
返回：
tensor([ 1.1552,  2.6148,  2.6535,  5.8318,  4.2361])

torch.normal(2, 3, size=(1, 4))
 
返回：
tensor([[-1.3987, -1.9544,  3.6048,  0.7909]])

 二、 运算

1.张量比较

对于x=Tensor([0,1,2,3,4])，返回满足的则为1（True），否为0（False）

torch.gt(x, 1)   大于  -> [0,0,1,1,1]

torch.ne(x, 1)   不等于  -> [1,0,1,1,1]

torch.lt(x, 3)   小于  -> [1，1，1，0，0]

torch.eq(x, 3)   等于  -> [0,0,0,1,0]

2. torch.eq

torch.pow(input, exponent, *, out=None) → Tensor

计算两个张量或者一个张量与一个标量的指数计算结果，返回一个张量。
input和exponent都可以是张量或者标量,
1)若input和exponent都为张量，则必须维度一致；
2)若input和exponent其中一个为标量，一个为张量，标量以广播的形式进行计算

>>> a = torch.randn(4)
>>> a
tensor([ 0.4331,  1.2475,  0.6834, -0.2791])
>>> torch.pow(a, 2)
tensor([ 0.1875,  1.5561,  0.4670,  0.0779])
>>> exp = torch.arange(1., 5.)
 
>>> a = torch.arange(1., 5.)
>>> a
tensor([ 1.,  2.,  3.,  4.])
>>> exp
tensor([ 1.,  2.,  3.,  4.])
>>> torch.pow(a, exp)
tensor([   1.,    4.,   27.,  256.])
 
>>> torch.pow(2, a)
tensor([ 2.,  4.,  8., 16.])
>>> torch.pow(a, 2)
tensor([ 1.,  4.,  9., 16.])

3. torch.sum

１．torch.sum(input, dtype=None)
２．torch.sum(input, list: dim, bool: keepdim=False, dtype=None) → Tensor

import torch

a = torch.ones((2, 3))
a1 =  torch.sum(a)
a2 =  torch.sum(a, dim=0)
a3 =  torch.sum(a, dim=1)

print(a)
print(a1)
print(a2)
print(a3)

4. torch.mean

求平均数。

mean()函数的参数：dim=0,按列求平均值，返回的形状是（1，列数）；dim=1,按行求平均值，返回的形状是（行数，1）,默认不设置dim的时候，返回的是所有元素的平均值。

x=torch.arange(12).view(4,3)
'''
注意：在这里使用的时候转一下类型，否则会报RuntimeError: Can only calculate the mean of floating types. Got Long instead.的错误。
查看了一下x元素类型是torch.int64,根据提示添加一句x=x.float()转为tensor.float32就行
'''
x=x.float()
x_mean=torch.mean(x)
x_mean0=torch.mean(x,dim=0,keepdim=True)
x_mean1=torch.mean(x,dim=1,keepdim=True)
print('x:')
print(x)
print('x_mean0:')
print(x_mean0)
print('x_mean1:')
print(x_mean1)
print('x_mean:')
print(x_mean)
x:
tensor([[ 0.,  1.,  2.],
        [ 3.,  4.,  5.],
        [ 6.,  7.,  8.],
        [ 9., 10., 11.]])
x_mean0:
tensor([[4.5000, 5.5000, 6.5000]])
x_mean1:
tensor([[ 1.],
        [ 4.],
        [ 7.],
        [10.]])
x_mean:
tensor(5.5000)

5. torch.mm

torch.mm(mat1, mat2, *, out=None) → Tensor

注意：mat1和mat1只能是矩阵matrix, 并且无法只用广播机制

6. torch.matmul

该方法支持张量乘法，可以实现广播机制

torch.matmul(input, other, *, out=None) → Tensor

7. torch.clamp

将输入input张量每个元素的夹紧到区间 [min,max]内，并返回结果到一个新张量。

torch.clamp(input, min, max, out=None) → Tensor
         | min, if input < min
output = | input, if min <= input <= max
         | max, if input > max

a=torch.randint(low=0,high=10,size=(10,1))
print(a)
a=torch.clamp(a,3,9)
print(a)
tensor([[9.],
        [3.],
        [0.],
        [4.],
        [4.],
        [2.],
        [4.],
        [1.],
        [2.],
        [9.]])
   
tensor([[9.],
        [3.],
        [3.],
        [4.],
        [4.],
        [3.],
        [4.],
        [3.],
        [3.],
        [9.]])

8. torch.max

torch.max(input, dim, max=None, max_indices=None) -> (Tensor, LongTensor)
返回输入张量给定维度上每行的最大值，并同时返回每个最大值的位置索引。
(返回的是最大值和索引！)

torch.max(input, other, out=None) → Tensor
返回输入张量给定维度上每行的最大值，并同时返回每个最大值的位置索引。 
即，( out_i=max(input_i,other_i) \)

9. torch.norm

torch.norm(input, p, dim, out=None,keepdim=False) → Tensor

返回输入张量给定维dim 上每行的p 范数。 

参数：

input (Tensor) – 输入张量
p (float) – 范数计算中的幂指数值
dim (int) – 缩减的维度
out (Tensor, optional) – 结果张量
keepdim（bool）– 保持输出的维度  （此参数官方文档中未给出，但是很常用）

10. torch.argmax

得到指定维度最大值的索引值。

1. torch.argmax(input, dim=None, keepdim=False)

import torch
a=torch.tensor(
              [
                  [1, 5, 5, 2],
                  [9, -6, 2, 8],
                  [-3, 7, -9, 1]
              ])
b=torch.argmax(a,dim=0)
print(b)
print(a.shape)

#tensor([1, 2, 0, 1])
#torch.Size([3, 4])

2. a.argmax(dim)

三、维度操作

1. torch.cat

即concatnate，将张量组合，拼接。

outputs = torch.cat(inputs, dim=?) → Tensor

>>> import torch
>>> A=torch.ones(2,3) #2x3的张量（矩阵）                                     
>>> A
tensor([[ 1.,  1.,  1.],
        [ 1.,  1.,  1.]])
>>> B=2*torch.ones(4,3)#4x3的张量（矩阵）                                    
>>> B
tensor([[ 2.,  2.,  2.],
        [ 2.,  2.,  2.],
        [ 2.,  2.,  2.],
        [ 2.,  2.,  2.]])
>>> C=torch.cat((A,B),0)#按维数0（行）拼接
>>> C
tensor([[ 1.,  1.,  1.],
         [ 1.,  1.,  1.],
         [ 2.,  2.,  2.],
         [ 2.,  2.,  2.],
         [ 2.,  2.,  2.],
         [ 2.,  2.,  2.]])
>>> C.size()
torch.Size([6, 3])
>>> D=2*torch.ones(2,4) #2x4的张量（矩阵）
>>> C=torch.cat((A,D),1)#按维数1（列）拼接
>>> C
tensor([[ 1.,  1.,  1.,  2.,  2.,  2.,  2.],
        [ 1.,  1.,  1.,  2.,  2.,  2.,  2.]])
>>> C.size()
torch.Size([2, 7])

2. torch.chunk

与cat相反，将张量拆分

torch.chunk(tensor, chunk_num, dim)

将tensor按dim（行或列）分割成chunk_num个tensor块，返回的是一个元组。

c = torch.tensor([[1., 2., 4.],
        [4., 5., 7.],
        [3., 9., 8.],
        [9., 6., 7.]])
 #在dim=1这一个维度进行拆分， chunk_num是拆分的块数，当其大于等于dim=1中元
 #素的个数n, 则拆成n块，小于则平分。
 torch.chunk(c,4,dim = 1)
 结果：
 (tensor([[1.],
         [4.],
         [3.],
         [9.]]),
 tensor([[2.],
         [5.],
         [9.],
         [6.]]),
 tensor([[4.],
         [7.],
         [8.],
         [7.]]))
torch.chunk(c,3,dim = 1)
结果：
(tensor([[1.],
         [4.],
         [3.],
         [9.]]),
 tensor([[2.],
         [5.],
         [9.],
         [6.]]),
 tensor([[4.],
         [7.],
         [8.],
         [7.]]))
torch.chunk(c,2,dim = 1)
结果：
(tensor([[1., 2.],
         [4., 5.],
         [3., 9.],
         [9., 6.]]),
 tensor([[4.],
         [7.],
         [8.],
         [7.]])) 

3. torch.squeeze和unqueeze

对维度进行压缩与扩充。

1）a.squeeze(N) 就是在a中指定位置N加上一个维数为1的维度。

2）b=torch.squeeze(a，N) a就是在a中指定位置N加上一个维数为1的维度

c = torch.tensor([[[1., 2., 4.],
        [4., 5., 7.],
        [3., 9., 8.],
        [9., 6., 7.]]])
c.shape
#torch.Size([1, 4, 3])
b = c.squeeze(0)
print(b, b.shape)
tensor([[1., 2., 4.],
        [4., 5., 7.],
        [3., 9., 8.],
        [9., 6., 7.]]) torch.Size([4, 3])