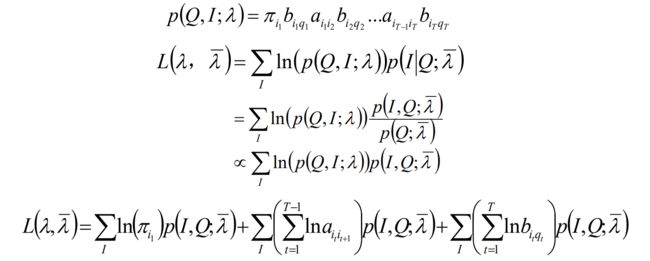马尔科夫系列——三、隐马尔可夫模型 - 学习问题 - Baum-Welch算法
转载的过程中发现,原文有些地方不太理解,就阅读了其他的文章,然后把代码的实现也引进来了。之前并没有验证代码的准确性,后面有人说,代码可能有问题,我尝试了修改。把简单修改版本的也放上来。
目录
一、训练数据包含观测序列和状态序列
1、初始概率的计算
2、转移概率的计算
3、发射概率
二、训练数据中只有观测序列
Baum-Welch算法 - π求解
Baum-Welch算法 - A求解
Baum-Welch算法 - B求解
代码实现
若训练数据包含观测序列和状态序列,则HMM的学习问题非常简单,是监督学习算法。
若训练数据只包含观测序列,则HMM的学习问题需要使用EM算法求解,是非监督学习算法。
一、训练数据包含观测序列和状态序列
直接利用大数定理的结论“频率的极限是概率”,直接给出HMM的参数估计;
下面一一给出解释和说明。
1、初始概率的计算
公式中|Si| : Si的个数,表示状态i的总个数;∑|Si|:表示所有时间点上的状态个数。举例如下图:
2、转移概率的计算
公式中aij 表示i号状态转移到j号状态的概率;|Sij| 表示i号状态转移到j号状态的个数;∑|Sij| 表示所有时间点上i号状态转移到j号状态的个数。举例如下图所示:
注意上图中的公式有点小问题,分母中的求和符号和sij中的j应该修改为其他的字母——如K,这样才没有歧义。
3、发射概率
bij 从当前状态转移到某个观测值的个数。
比如从1号盒子这个状态,转移到取出白球这个观测值的可能性 = b1白;
b1白 = (1->白)的个数 / [(1->白)的个数+(1->黑)的个数]
同样的它的公式中分母中的求和符号和qij中的J应该修改为其他的字母——如k,这样才更好理解。
二、训练数据中只有观测序列
只有观测序列,没有状态序列,这个时候就得采用Baum-Welch算法。本文中的Baum-Welch算法解释写的不是很详细,具体的推导和实现需要参考别的博客——隐马尔可夫模型之Baum-Welch算法详解和”相亲记“之从EM算法到Baum-Welch算法。在Baum-Welch算法的推导过程中需要用到EM算法的原理和HMM概率问题中的前向和后向算法结论。
根据EM算法的E步:得到Q函数,然后对Q函数极大化,
Baum-Welch算法 - π求解
极大化L,使用拉格朗日乘子法,求解π的值:
Baum-Welch算法 - A求解
极大化L,使用拉格朗日乘子法,求解aij的值:
Baum-Welch算法 - B求解
极大化L,使用拉格朗日乘子法,求解bij的值:
Baum-Welch算法 - 极大化L函数,分别可以求得π、a、b的值
其中:
![]()
![]()
代码实现
来自这篇博文:”相亲记“之从EM算法到Baum-Welch算法,理解代码可以配合博文大学食堂之HMM模型(三)——Baum-Walch算法来进行——我还没有来得及去验证这个代码,以后有机会在验证,先把HMM的理论理解了进入CRF中,CRF才是最重要的,目前对我来说!
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import numpy
'''
Created on 2017年2月9日
@author: 薛沛雷
'''
class HMM:
def __init__(self,A,B,Pi):
self.A=A
self.B=B
self.Pi=Pi
#前向算法
def forward(self,O):
row=self.A.shape[0]
col=len(O)
alpha=numpy.zeros((row,col))
#初值
alpha[:,0]=self.Pi*self.B[:,O[0]]
#递推
for t in range(1,col):
for i in range(row):
alpha[i,t]=numpy.dot(alpha[:,t-1],self.A[:,i])*self.B[i,O[t]]
#终止
return alpha
#后向算法
def backward(self,O):
row=self.A.shape[0]
col=len(O)
beta=numpy.zeros((row,col))
#初值
beta[:,-1:]=1
#递推
for t in reversed(range(col-1)):
for i in range(row):
beta[i,t]=numpy.sum(self.A[i,:]*self.B[:,O[t+1]]*beta[:,t+1])
#终止
return beta
#前向-后向算法(Baum-Welch算法):由 EM算法 & HMM 结合形成
def baum_welch(self,O,e=0.05):
row=self.A.shape[0]
col=len(O)
done=False
while not done:
zeta=numpy.zeros((row,row,col-1))
alpha=self.forward(O)
beta=self.backward(O)
#EM算法:由 E-步骤 和 M-步骤 组成
#E-步骤:计算期望值zeta和gamma
for t in range(col-1):
#分母部分
denominator=numpy.dot(numpy.dot(alpha[:,t],self.A)*self.B[:,O[t+1]],beta[:,t+1])
for i in range(row):
#分子部分以及zeta的值
numerator=alpha[i,t]*self.A[i,:]*self.B[:,O[t+1]]*beta[:,t+1]
zeta[i,:,t]=numerator/denominator
gamma=numpy.sum(zeta,axis=1)
final_numerator=(alpha[:,col-1]*beta[:,col-1]).reshape(-1,1)
final=final_numerator/numpy.sum(final_numerator)
gamma=numpy.hstack((gamma,final))
#M-步骤:重新估计参数Pi,A,B
newPi=gamma[:,0]
newA=numpy.sum(zeta,axis=2)/numpy.sum(gamma[:,:-1],axis=1)
newB=numpy.copy(self.B)
b_denominator=numpy.sum(gamma,axis=1)
temp_matrix=numpy.zeros((1,len(O)))
for k in range(self.B.shape[1]):
for t in range(len(O)):
if O[t]==k:
temp_matrix[0][t]=1
newB[:,k]=numpy.sum(gamma*temp_matrix,axis=1)/b_denominator
#终止阀值
if numpy.max(abs(self.Pi-newPi))以上代码,最后的结果中P的概率之和为1.A的和B的每行概率之和明显不是1,这里可能就有点问题了。我做了简单的修改,只是修改了一句代码,PAB的各自概率之和差不多都近似为1了。
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import numpy
import numpy as np
'''
Created on 2020-04-18
@author: HY
'''
class HMM:
def __init__(self, A, B, Pi):
self.A = A
self.B = B
self.Pi = Pi
# 前向算法
def forward(self, O):
row = self.A.shape[0]
col = len(O)
alpha = numpy.zeros((row, col))
# 初值
alpha[:, 0] = self.Pi * self.B[:, O[0]]
# 递推
for t in range(1, col):
for i in range(row):
alpha[i, t] = numpy.dot(alpha[:, t - 1], self.A[:, i]) * self.B[i, O[t]]
# 终止
return alpha
# 后向算法
def backward(self, O):
row = self.A.shape[0]
col = len(O)
beta = numpy.zeros((row, col))
# 初值
beta[:, -1:] = 1
# 递推
for t in reversed(range(col - 1)):
for i in range(row):
# beta[i, t] = numpy.sum(self.A[i, :] * self.B[:, O[t + 1]] * beta[:, t + 1])
beta[i, t] = numpy.dot(beta[:, t + 1],self.A[i,:])* self.B[i,O[t + 1]]
# 终止
return beta
# 前向-后向算法(Baum-Welch算法):由 EM算法 & HMM 结合形成
def baum_welch(self, observations, criterion=0.05):
n_states = self.A.shape[0]
# 观察序列的长度T
n_samples = len(observations)
done = False
while not done:
# alpha_t(i) = P(o_1,o_2,...,o_t,q_t = s_i | hmm)
# Initialize alpha
# 获得所有前向传播节点值 alpha_t(i)
alpha = self.forward(observations)
# beta_t(i) = P(o_t+1,o_t+2,...,o_T | q_t = s_i , hmm)
# Initialize beta
# 获得所有后向传播节点值 beta_t(i)
beta = self.backward(observations)
# 计算 xi_t(i,j) -> xi(i,j,t)
xi = np.zeros((n_states, n_states, n_samples - 1))
# 在每个时刻
for t in range(n_samples - 1):
# 计算P(O | hmm)
denom = sum(alpha[:, -1])
for i in range(n_states):
# numer[1,:] = 行向量,alpha[i,t]=实数,slef.A[i,:] = 行向量
# self.B[:,observations[t+1]].T = 行向量,beta[:,t+1].T = 行向量
numer = alpha[i, t] * self.A[i, :] * self.B[:, observations[t + 1]].T * beta[:, t + 1].T
xi[i, :, t] = numer / denom
# 计算gamma_t(i) 就是对j进行求和
gamma = np.sum(xi, axis=1)
# need final gamma elements for new B
prod = (alpha[:, n_samples - 1] * beta[:, n_samples - 1]).reshape((-1, 1))
# 合并T时刻的节点
gamma = np.hstack((gamma, prod / np.sum(prod)))
# 列向量
newpi = gamma[:, 0]
newA = np.sum(xi, 2) / np.sum(gamma[:, :-1], axis=1).reshape((-1, 1))
newB = np.copy(self.B)
# 观测状态
num_levels = self.B.shape[1]
sumgamma = np.sum(gamma, axis=1)
temp_matrix = numpy.zeros((1, len(observations)))
for lev in range(num_levels):
for t in range(len(observations)):
if observations[t]== lev:
temp_matrix[0][t] = 1
newB[:, lev] = np.sum(gamma*temp_matrix, axis=1) / sumgamma
temp_matrix = numpy.zeros((1, len(observations)))
if np.max(abs(self.Pi - newpi)) < criterion and np.max(abs(self.A - newA)) < criterion and np.max(abs(self.B - newB)) < criterion:
done = 1
self.A[:], self.B[:], self.Pi = newA, newB, newpi
return self.Pi, self.A, self.B
# 将字典转化为矩阵
def matrix(X, index1, index2):
# 初始化为0矩阵
m = numpy.zeros((len(index1), len(index2)))
for row in X:
for col in X[row]:
# 转化
m[index1.index(row)][index2.index(col)] = X[row][col]
return m
if __name__ == "__main__":
# 初始化,随机的给参数A,B,Pi赋值
status = ["相处", "拜拜"]
observations = ["撒娇", "低头玩儿手机", "眼神很友好", "主动留下联系方式"] # 撒娇:小拳拳捶你胸口
A = {"相处": {"相处": 0.5, "拜拜": 0.5}, "拜拜": {"相处": 0.5, "拜拜": 0.5}}
B = {"相处": {"撒娇": 0.4, "低头玩儿手机": 0.1, "眼神很友好": 0.3, "主动留下联系方式": 0.2},
"拜拜": {"撒娇": 0.1, "低头玩儿手机": 0.5, "眼神很友好": 0.2, "主动留下联系方式": 0.2}}
Pi = [0.5, 0.5]
Ob = [1,2,0,2,3,0]
A = matrix(A, status, status)
B = matrix(B, status, observations)
hmm = HMM(A, B, Pi)
p = hmm.baum_welch(Ob)[0]
a = hmm.baum_welch(Ob)[1]
b = hmm.baum_welch(Ob)[2]
print('p:',p)
print('a:',a)
print('b:',b)最后的结果: