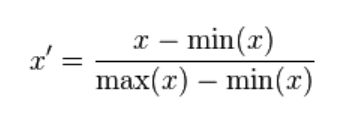基于python的数据分析

基于python的数据分析

1.数据集

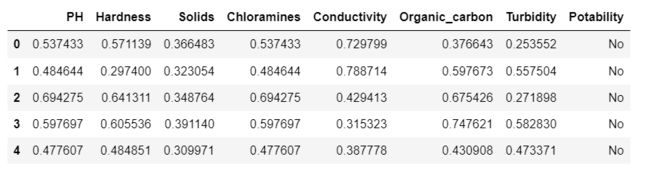
本数据集是关于不同水体的水质指标的信息，如下所示：

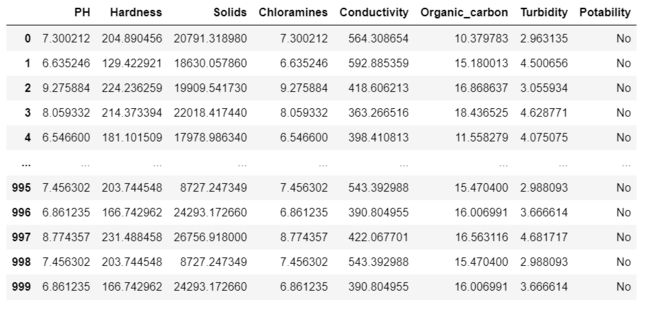
其中，PH : 评价水体酸碱平衡的一个重要参数
Hardness : 水的硬度，用水析出毫克/升肥皂的能力表征
Solids : 总溶解固体含量
Chloramines : 氯胺含量（%）
Conductivity : 传导性，电导率以微秒/厘米为单位
Organic_carbon : 有机碳含量（%）
Turbidity : 浑浊度
Potability : 指示人类是否可安全饮用水，其中No表示可饮用水，Yes表示不可饮用水，即为标签值。

2.使用matplotlib对数据集进行可视化

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
#把不同标签用颜色区分
Colors = []
for i in range(WaterData.shape[0]):
    m = WaterData.iloc[i,-1]
    if m=='No':
        Colors.append('orange')
    if m=='Yes':
        Colors.append('red')
        
#绘制两两特征之间的散点图        
pl=plt.figure(figsize=(15,8))
fig1=pl.add_subplot(221)
plt.scatter(WaterData.iloc[:,0],WaterData.iloc[:,6],marker='.',c=Colors)
plt.xlabel('PH ')
plt.ylabel('Chloramines ')

fig2=pl.add_subplot(222)
plt.scatter(WaterData.iloc[:,3],WaterData.iloc[:,5],marker='.',c=Colors)
plt.xlabel('Chloramines')
plt.ylabel('Organic_carbon')

fig3=pl.add_subplot(223)
plt.scatter(WaterData.iloc[:,1],WaterData.iloc[:,4],marker='.',c=Colors)
plt.xlabel('Hardness')
plt.ylabel('Conductivity')

fig4=pl.add_subplot(224)
plt.scatter(WaterData.iloc[:,5],WaterData.iloc[:,6],marker='.',c=Colors)
plt.xlabel('Organic_carbon')
plt.ylabel('Turbidity')

plt.show()

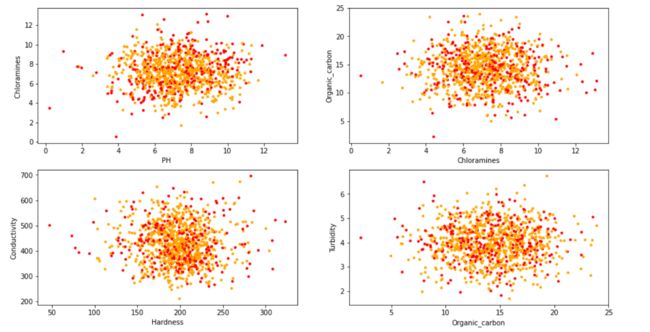
图一表示PH值和浑浊度对水质的影响，黄色点代表不可饮用水，红点代表可饮用水，可以看到在PH值4~10之间，氯胺含量百分之3 ~10之间，不可饮用水的分布远大于可饮用水的分布，可知这两个特征对水质的影响较大；图二、三同理，图四横坐标为有机碳含量，纵坐标为浑浊度，可以观察到可饮用水和不可饮用水大致均匀分布，即这两个特征对水质影响较小。

3.对K-近邻算法的理解

3.1 K-近邻算法简介

如果一个数据集中的数据具有若干个特征和一个标签值，即每个数据都有其对应的分类，那么就可以用KNN的方法对数据进行训练。当输入一个没有标签的数据后，将新数据中的每个特征与样本集中数据对应的特征进行比较，提取出样本集中特征最相似数据（最近邻）的分类标签。
具体来说就是计算待标记样本和数据集中每个样本的欧式距离，取距离最近的k个样本。这k个样本的多数属于某个分类，就把该代标记样本分到这个类中（少数服从多数）。

3.2 KNN算法的一般流程：

1）数据预处理；
2）计算测试数据与各个训练数据之间的距离；
3）按照距离的递增关系进行排序；
4）选取距离最小的K个点；
5）确定前K个点所在类别的出现频率；
6）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

3.3 K的取值

k值越大，模型的偏差越大，对噪声数据越不敏感，当k值很大时，可能造成欠拟合；
k值越小，模型的方差就会越大，当k值太小，就会造成过拟合。
一般使用交叉验证的方法，针对于不同的K，训练集训练模型，测试集验证K值得合理性，具体需要实验调整参数确定。

4.数据预处理

4.1 归一化

由于在本数据集中溶解固体含量（Solids）与其他特征相差数倍(如下图)，那么在计算距离时，会偏向于Solids这个特征，这样造成各个特征并不是等价重要的，最终可能会导致距离计算错误，从而导致预测错误。
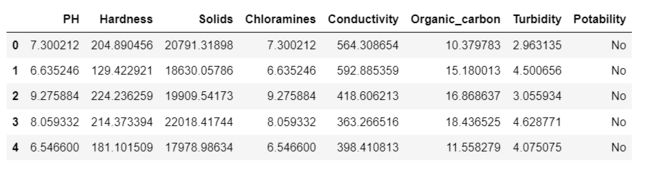因此需要对各个特征统一量纲，也就是数据归一化。

def minmax(data):       # 归一化
    mindata=data.min()
    maxdata = data.max()
    newd = (data-mindata)/(maxdata-mindata)
    return newd
Water= pd.concat([minmax(WaterData.iloc[:,:7]),WaterData.iloc[:,-1]],axis=1)
Water.head()

这里用到了线性归一化方法，如下

归一化结果：

4.2 标签编码

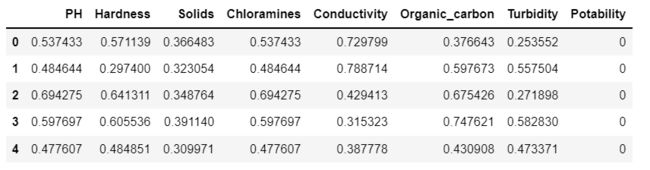
由于标签值是用字符串的形式表示的，我们需要对标签编码，便于计算机处理。用0表示"No"，1表示"Yes"，如下所示：

lbe = preprocessing.LabelEncoder()  #标签编码  
Water.iloc[:,-1] = lbe.fit_transform(Water.iloc[:,-1])  #  0 NO 1 Yes 
Water.head()

4.3 划分训练集和测试集

X = Water.iloc[:,:7]   
Y = Water.iloc[:,-1]  #  用X表示特征值，Y表示标签值
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,Y,test_size=0.3)  # 划分训练集和测试集（随机），顺序不能改变

这个过程是随机划分的，数据的索引值被打乱，恢复索引：

for i in [Xtrain,Xtest,Ytrain,Ytest]:
    i.index = range(i.shape[0])      #恢复索引

5.模型实例化

建立模型

knn = KNeighborsClassifier(n_neighbors = 15)     #模型启动
knn.fit(Xtrain,Ytrain)    #拟合训练集

验证一下，若用全部数据的均值代入模型，我们的模型会给出什么结果
in:

mean = X.mean().values   #求数据均值
mean

out:

array([0.5441423 , 0.54714393, 0.38791914, 0.52590446, 0.44915194,
       0.55432462, 0.45292746])

将数据代入模型：
in:

mean = mean.reshape(1,-1)   #转换数据矩阵形态
knn.predict(mean)

out:

array([0])

返回的矩阵0代表了这是不可饮用水。

6.参数分析

将测试集代入模型，用score函数看看预测的结果准确与否。
in：

acc_knn = knn.score(Xtest,Ytest)
acc_knn

out:

0.72

评分为0.72，准确率较低，可能是由于原数据集数据量太大，为了便于观察我进行了一些删改导致的。

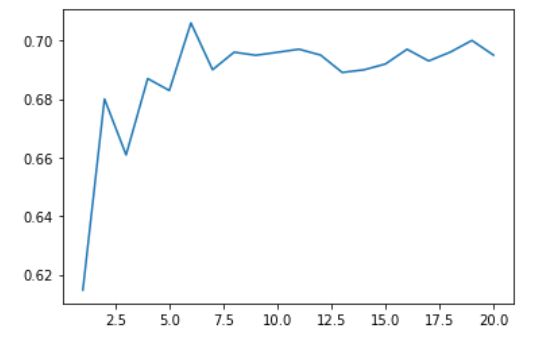
画出学习曲线

1.对于模型若使用不同的k值，会使得准确率发生什么变化？

#对于不同的k值
score = []
for k in range(1,21):
    knn = KNeighborsClassifier(n_neighbors = k)  #实例化
    cvs = cross_val_score(knn,X,Y,cv=20)  #交叉验证
    score.append(cvs.mean())
plt.plot([*range(1,21)],score)    
plt.show()

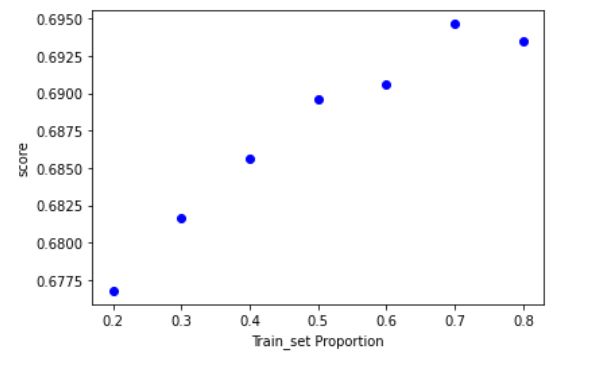
2.在使用train_test_split()函数划分数据集时，若使用不同的比例划分训练集和测试集，结果会发生什么变化？

#使用不同比例的划分训练集对结果的影响
proportion = [0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2]
knn = KNeighborsClassifier(n_neighbors = 15)
socres = []
plt.figure()
for p in proportion:
    scores = []
    for i in range(1,100):
        Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,Y,test_size = 1-p)
        knn.fit(Xtrain,Ytrain)
        scores.append(knn.score(Xtest,Ytest))
    plt.plot(p,np.mean(scores),'bo')
    plt.xlabel('Train_set Proportion')
    plt.ylabel('score')

可以看到对训练集比例的划分也会影响准确率。