%--------------------------------------------------------------------------
% 回归分析
%--------------------------------------------------------------------------
%% examp19.1-1
mdl = LinearModel;
methods(mdl)
properties(mdl)
%% examp19.1-2
nlm = NonLinearModel
methods(nlm)
properties(nlm)
%% examp19.2-1 一元线性回归
ClimateData = xlsread('examp19_2_1.xls');
x = ClimateData(:, 1);
y = ClimateData(:, 5);
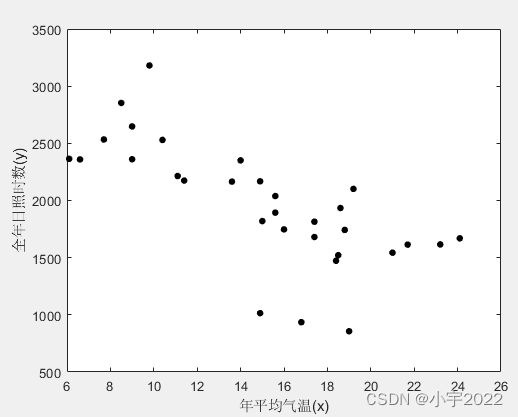
figure;
plot(x, y, 'k.', 'Markersize', 15);
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
R = corrcoef(x, y)
mdl1 = LinearModel.fit(x,y)
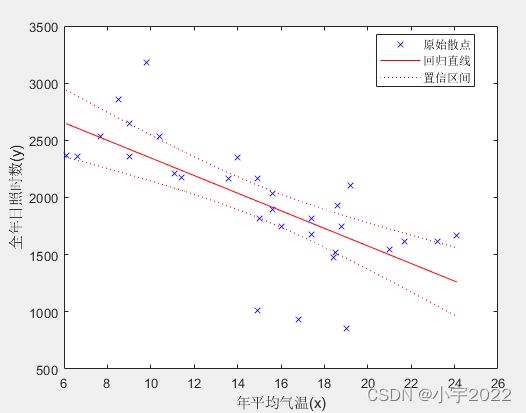
figure;
mdl1.plot
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
title('');
legend('原始散点','回归直线','置信区间');
xnew = [5,25]';
ynew = mdl1.predict(xnew)
Res = mdl1.Residuals;
Res_Stu = Res.Studentized;
Res_Stan = Res.Standardized;
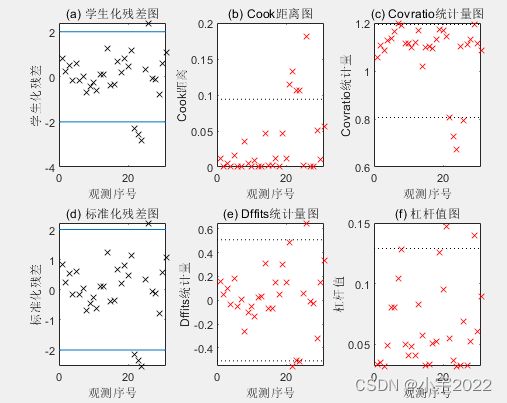
figure;
subplot(2,3,1);
plot(Res_Stu,'kx');
refline(0,-2);
refline(0,2);
title('(a) 学生化残差图')
xlabel('观测序号');ylabel('学生化残差');
subplot(2,3,2);
mdl1.plotDiagnostics('cookd');
title('(b) Cook距离图')
xlabel('观测序号');ylabel('Cook距离');
subplot(2,3,3);
mdl1.plotDiagnostics('covratio');
title('(c) Covratio统计量图');
xlabel('观测序号');ylabel('Covratio统计量');
subplot(2,3,4);
plot(Res_Stan,'kx');
refline(0,-2);
refline(0,2);
title('(d) 标准化残差图');
xlabel('观测序号');ylabel('标准化残差');
subplot(2,3,5);
mdl1.plotDiagnostics('dffits');
title('(e) Dffits统计量图');
xlabel('观测序号');ylabel('Dffits统计量');
subplot(2,3,6);
mdl1.plotDiagnostics('leverage');
title('(f) 杠杆值图');
xlabel('观测序号');ylabel('杠杆值');
id = find(abs(Res_Stu)>2);
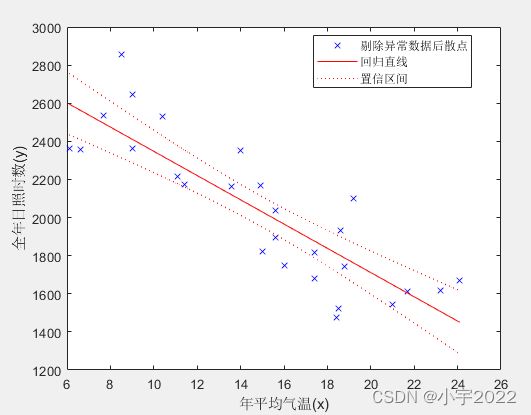
mdl2 = LinearModel.fit(x,y,'Exclude',id)
figure;
mdl2.plot;
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
title('');
legend('剔除异常数据后散点','回归直线','置信区间');
figure; % 新建一个图形窗口
plot(x, y, 'ko'); % 画原始数据散点
hold on; % 图形叠加
xnew = sort(x); % 为了画图的需要将x从小到大排序
yhat1 = mdl1.predict(xnew); % 计算模型1的拟合值
yhat2 = mdl2.predict(xnew); % 计算模型2的拟合值
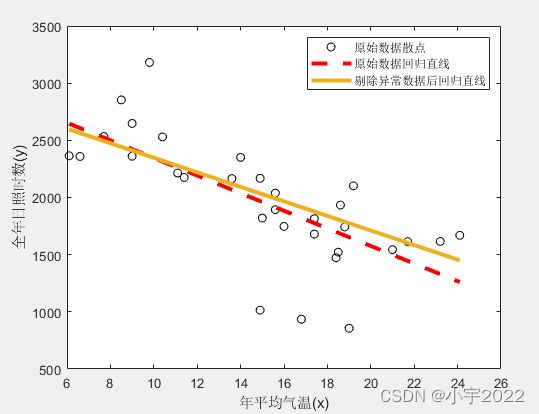
plot(xnew, yhat1, 'r--','linewidth',3); % 画原始数据对应的回归直线,红色虚线
plot(xnew, yhat2, 'linewidth', 3); % 画剔除异常数据后的回归直线,蓝色实线
legend('原始数据散点','原始数据回归直线','剔除异常数据后回归直线') % 为图形加标注框
xlabel('年平均气温(x)'); % 为X轴加标签
ylabel('全年日照时数(y)');
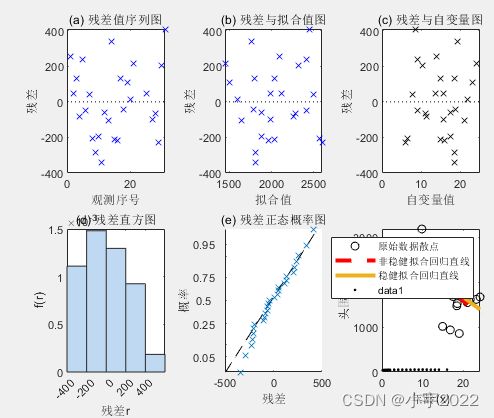
figure;
subplot(2,3,1);
mdl2.plotResiduals('caseorder');
title('(a) 残差值序列图');
xlabel('观测序号');ylabel('残差');
subplot(2,3,2);
mdl2.plotResiduals('fitted');
title('(b) 残差与拟合值图');
xlabel('拟合值');ylabel('残差');
subplot(2,3,3);
plot(x,mdl2.Residuals.Raw,'kx');
line([0,25],[0,0],'color','k','linestyle',':');
title('(c) 残差与自变量图');
xlabel('自变量值');ylabel('残差');
subplot(2,3,4);
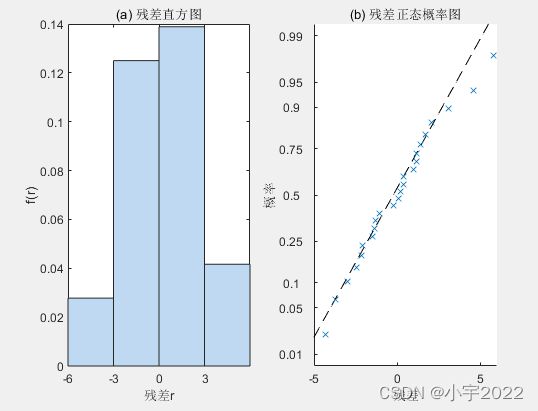
mdl2.plotResiduals('histogram');
title('(d) 残差直方图');
xlabel('残差r');ylabel('f(r)');
subplot(2,3,5);
mdl2.plotResiduals('probability');
title('(e) 残差正态概率图');
xlabel('残差');ylabel('概率');
subplot(2,3,6);
mdl2.plotResiduals('lagged');
title('(f) 残差与滞后残差图');
xlabel('滞后残差');ylabel('残差');
mdl3 = LinearModel.fit(x,y,'RobustOpts','on')
xnew = sort(x);
yhat1 = mdl1.predict(xnew);
yhat3 = mdl3.predict(xnew);
plot(x, y, 'ko');
hold on;
plot(xnew, yhat1, 'r--','linewidth',3);
plot(xnew, yhat3, 'linewidth', 3);
legend('原始数据散点','非稳健拟合回归直线','稳健拟合回归直线');
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
%% examp19.3-1 一元非线性回归
HeadData = xlsread('examp19_3_1.xls');
x = HeadData(:, 4);
y = HeadData(:, 9);
plot(x, y, 'k.');
xlabel('年龄(x)');
ylabel('头围(y)');
HeadCir2 = @(beta, x)beta(1)*exp(beta(2)./(x+beta(3)));
beta0 = [53,-0.2604,0.6276];
opt = statset;
opt.Robust = 'on';
nlm1 = NonLinearModel.fit(x,y,HeadCir2,beta0,'Options',opt)
%或nlm1 = NonLinearModel.fit(x,y,@HeadCir1,beta0,'Options',opt)
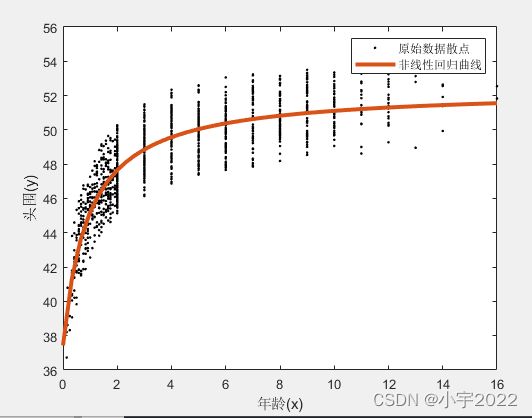
xnew = linspace(0,16,50)';
ynew = nlm1.predict(xnew);
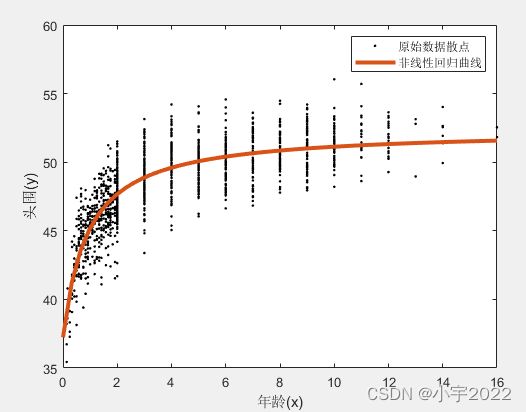
figure;
plot(x, y, 'k.');
hold on;
plot(xnew, ynew, 'linewidth', 3);
xlabel('年龄(x)');
ylabel('头围(y)');
legend('原始数据散点','非线性回归曲线');
Alpha = 0.05;
ci1 = nlm1.coefCI(Alpha)
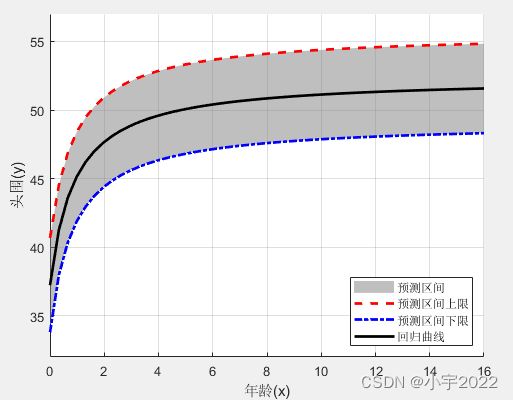
[yp,ypci] = nlm1.predict(xnew,'Prediction','observation');
yup = ypci(:,2);
ydown = ypci(:,1);
figure;
hold on;
h1 = fill([xnew;flipud(xnew)],[yup;flipud(ydown)],[0.5,0.5,0.5]);
set(h1,'EdgeColor','none','FaceAlpha',0.5);
plot(xnew,yup,'r--','LineWidth',2);
plot(xnew,ydown,'b-.','LineWidth',2);
plot(xnew, yp, 'k','linewidth', 2);
grid on;
ylim([32, 57]);
xlabel('年龄(x)');
ylabel('头围(y)');
h2 = legend('预测区间','预测区间上限','预测区间下限','回归曲线');
set(h2, 'Location', 'SouthEast');
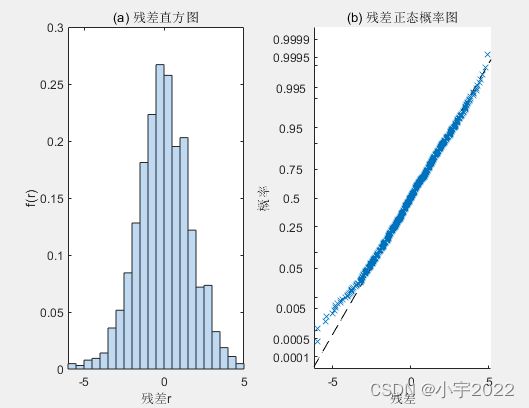
figure;
subplot(1,2,1);
nlm1.plotResiduals('histogram');
title('(a) 残差直方图');
xlabel('残差r');ylabel('f(r)');
subplot(1,2,2);
nlm1.plotResiduals('probability');
title('(b) 残差正态概率图');
xlabel('残差');ylabel('概率');
Res2 = nlm1.Residuals;
Res_Stu2 = Res2.Studentized;
id2 = find(abs(Res_Stu2)>2);
nlm2 = NonLinearModel.fit(x,y,HeadCir2,beta0,'Exclude',id2,'Options',opt)
xb = x; xb(id2) = [];
yb = y; yb(id2) = [];
ynew = nlm2.predict(xnew);
figure;
plot(xb, yb, 'k.');
hold on;
plot(xnew, ynew, 'linewidth', 3);
xlabel('年龄(x)');
ylabel('头围(y)');
legend('原始数据散点','非线性回归曲线');
%% examp19.4-1 多元线性和广义线性回归
data = xlsread('examp19_4_1.xls');
X = data(:,3:7);
y = data(:,2);
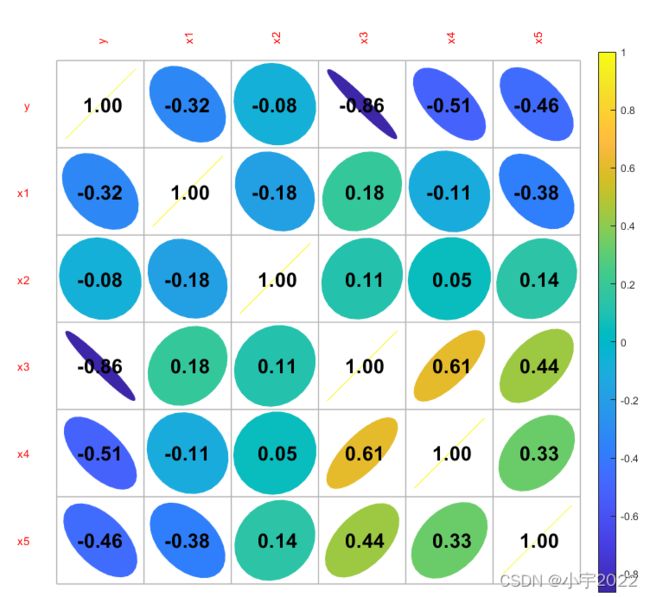
[R,P] = corrcoef([y,X])
VarNames = {'y','x1','x2','x3','x4','x5'};
matrixplot(R,'FigShap','e','FigSize','Auto', ...
'ColorBar','on','XVar', VarNames,'YVar',VarNames);
mmdl1 = LinearModel.fit(X,y)
Rx = corrcoef(X);
VIF = diag(inv(Rx))
figure;
subplot(1,2,1);
mmdl1.plotResiduals('histogram');
title('(a) 残差直方图');
xlabel('残差r');ylabel('f(r)');
subplot(1,2,2);
mmdl1.plotResiduals('probability');
title('(b) 残差正态概率图');
xlabel('残差');ylabel('概率');
Res3 = mmdl1.Residuals;
Res_Stu3 = Res3.Studentized;
id3 = find(abs(Res_Stu3)>2);
Model = 'poly10101';
mmdl2 = LinearModel.fit(X,y,Model,'Exclude',id3)
Model = 'poly22222';
mmdl3 = LinearModel.fit(X,y,Model)
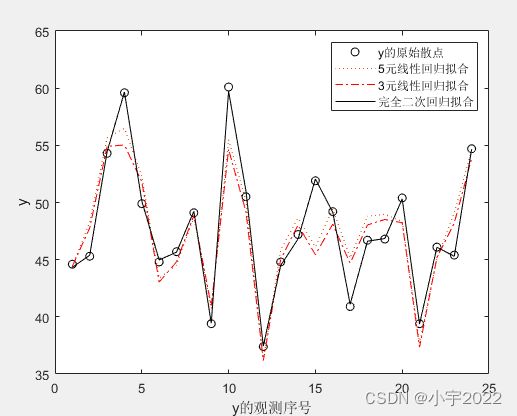
figure;
plot(y,'ko');
hold on
plot(mmdl1.predict(X),':');
plot(mmdl2.predict(X),'r-.');
plot(mmdl3.predict(X),'k');
legend('y的原始散点','5元线性回归拟合',...
'3元线性回归拟合','完全二次回归拟合');
xlabel('y的观测序号');
ylabel('y');
mmdl4 = LinearModel.stepwise(X,y, 'poly22222')
yfitted = mmdl4.Fitted;
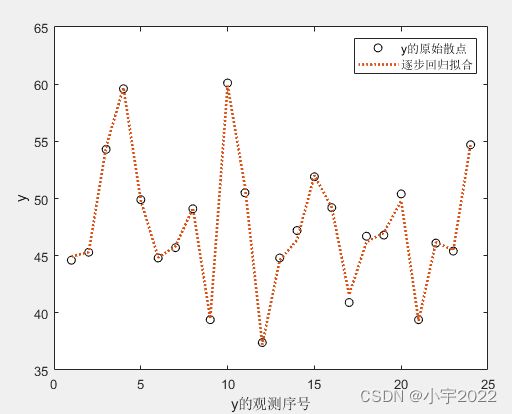
figure;
plot(y,'ko');
hold on
plot(yfitted,':','linewidth',2);
legend('y的原始散点','逐步回归拟合');
xlabel('y的观测序号');
ylabel('y');
model = [0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 0 0 1
2 0 0 0 0
1 1 0 0 0
0 1 1 0 0
1 0 0 1 0
0 0 0 2 0
1 0 0 0 1
0 1 0 0 1
0 0 1 0 1
0 0 0 0 2];
mmdl5 = LinearModel.fit(X,y,model)
%% examp19.5-1 多元非线性回归
modelfun = @(b,x)sqrt((x(:,1)-b(1)).^2+(x(:,2)-b(2)).^2+b(3).^2)/(60*b(4))+b(5);
% modelfun = 'y ~ sqrt((x1-b1)^2 + (x2-b2)^2 + b3^2)/(60*b4)+b5';
xyt = [500 3300 21 9
300 200 19 29
800 1600 14 51
1400 2200 13 17
1700 700 11 46
2300 2800 14 47
2500 1900 10 14
2900 900 11 46
3200 3100 17 57
3400 100 16 49];
xy = xyt(:,1:2); Minutes = xyt(:,3); Seconds = xyt(:,4);
T = Minutes + Seconds/60;
b0 = [1000 100 1 1 1];
mnlm = NonLinearModel.fit(xy,T,modelfun,b0) ```
```clike
mdl =
线性回归模型:
y ~ 0
系数:
逻辑 "与" (&&)和 "或" (||)运算符的操作数必须可转换为标量逻辑值。
出错 classreg.regr.CompactLinearModel/dispBody (第 533 行)
if model.MSE>0 && ~isnan(model.MSE)
出错 LinearModel/disp (第 294 行)
dispBody(model)
出错 Chapter19 (第 8 行)
mdl = LinearModel
```bash
function y = HeadCir1(beta, x)
% CopyRight:xiezhh
y = beta(1) * exp(beta(2) ./ (x + beta(3)));``
`
```handlebars
function matrixplot(data,varargin)
% 根据实值矩阵绘制色块图,用丰富的颜色和形状形象的展示矩阵元素值的大小。
%
% matrixplot(data) 绘制矩阵色块图,data为实值矩阵,每一个元素对应一个色块,色
% 块颜色由元素值大小决定。
%
% matrixplot(data, 'PARAM1',val1, 'PARAM2',val2, ...)
% 用成对出现的参数名/参数值控制色块的各项属性。可用的参数名/参数值如下:
% 'FigShape' --- 设定色块的形状,其参数值为:
% 'Square' --- 方形(默认)
% 'Circle' --- 圆形
% 'Ellipse' --- 椭圆形
% 'Hexagon' --- 六边形
% 'Dial' --- 表盘形
%
% 'FigSize' --- 设定色块的大小,其参数值为:
% 'Full' --- 最大色块(默认)
% 'Auto' --- 根据矩阵元素值自动确定色块大小
%
% 'FigStyle' --- 设定矩阵图样式,其参数值为:
% 'Auto' --- 矩形矩阵图(默认)
% 'Tril' --- 下三角矩阵图
% 'Triu' --- 上三角矩阵图
%
% 'FillStyle' --- 设定色块填充样式,其参数值为:
% 'Fill' --- 填充色块内部(默认)
% 'NoFill' --- 不填充色块内部
%
% 'DisplayOpt' --- 设定是否在色块中显示矩阵元素值,其参数值为:
% 'On' --- 显示矩阵元素值(默认)
% 'Off' --- 不显示矩阵元素值
%
% 'TextColor' --- 设定文字的颜色,其参数值为:
% 表示单色的字符('r','g','b','y','m','c','w','k'),默认为黑色
% 1行3列的红、绿、蓝三元色灰度值向量([r,g,b])
% 'Auto' --- 根据矩阵元素值自动确定文字颜色
%
% 'XVarNames' --- 设定X轴方向需要显示的变量名(默认为X1,X2,...),其参数值为:
% 字符串矩阵或字符串元胞数组,若为字符串矩阵,其行数应与data的列数相同
% 若为字符串元胞数组,其长度应与data的列数相同。
%
% 'YVarNames' --- 设定Y轴方向需要显示的变量名(默认为Y1,Y2,...),其参数值为:
% 字符串矩阵或字符串元胞数组,若为字符串矩阵,其行数应与data的行数相同
% 若为字符串元胞数组,其长度应与data的行数相同。
%
% 'ColorBar' --- 设定是否显示颜色条,其参数值为:
% 'On' --- 显示颜色条
% 'Off' --- 不显示颜色条(默认)
%
% 'Grid' --- 设定是否显示网格线,其参数值为:
% 'On' --- 显示网格线(默认)
% 'Off' --- 不显示网格线
%
% Example:
% x = [1,-0.2,0.3,0.8,-0.5
% -0.2,1,0.6,-0.7,0.2
% 0.3,0.6,1,0.5,-0.3
% 0.8,-0.7,0.5,1,0.7
% -0.5,0.2,-0.3,0.7,1];
% matrixplot(x);
% matrixplot(x,'DisplayOpt','off');
% matrixplot(x,'FillStyle','nofill','TextColor','Auto');
% matrixplot(x,'TextColor',[0.7,0.7,0.7],'FigShap','s','FigSize','Auto','ColorBar','on');
% matrixplot(x,'TextColor','k','FigShap','d','FigSize','Full','ColorBar','on','FigStyle','Triu');
% XVarNames = {'xiezhh','heping','keda','tust','tianjin'};
% matrixplot(x,'FigShap','e','FigSize','Auto','ColorBar','on','XVarNames',XVarNames,'YVarNames',XVarNames);
%
% CopyRight:xiezhh(谢中华),2013.01.24编写
% 对第一个输入参数类型进行判断
if ~ismatrix(data) || ~isreal(data)
error('输入参数类型不匹配:第一个输入参数应为实值矩阵');
end
% 解析成对出现的参数名/参数值
[FigShape,FigSize,FigStyle,FillStyle,DisplayOpt,TextColor,XVarNames,...
YVarNames,ColorBar,GridOpt] = parseInputs(varargin{:});
% 产生网格数据
[m,n] = size(data);
[x,y] = meshgrid(0:n,0:m);
data = data(:);
maxdata = nanmax(data);
mindata = nanmin(data);
rangedata = maxdata - mindata;
if isnan(rangedata)
warning('MATLAB:warning1','请检查您输入的矩阵是否合适!');
return;
end
z = zeros(size(x))+0.2;
sx = x(1:end-1,1:end-1)+0.5;
sy = y(1:end-1,1:end-1)+0.5;
if strncmpi(FigStyle,'Tril',4)
z(triu(ones(size(z)),2)>0) = NaN;
sx(triu(ones(size(sx)),1)>0) = NaN;
elseif strncmpi(FigStyle,'Triu',4)
z(tril(ones(size(z)),-2)>0) = NaN;
sx(tril(ones(size(sx)),-1)>0) = NaN;
end
sx = sx(:);
sy = sy(:);
id = isnan(sx) | isnan(data);
sx(id) = [];
sy(id) = [];
data(id) = [];
if isempty(XVarNames)
XVarNames = strcat('X',cellstr(num2str((1:n)')));
else
if (iscell(XVarNames) && (numel(XVarNames) ~= n)) || (~iscell(XVarNames) && (size(XVarNames,1) ~= n))
error('X轴方向变量名应为字符串矩阵或字符串元胞数组,其长度与输入矩阵的列数相同');
end
end
if isempty(YVarNames)
YVarNames = strcat('Y',cellstr(num2str((1:m)')));
else
if (iscell(YVarNames) && (numel(YVarNames) ~= m)) || (~iscell(YVarNames) && (size(YVarNames,1) ~= m))
error('Y轴方向变量名应为字符串矩阵或字符串元胞数组,其长度与输入矩阵的行数相同');
end
end
% 绘图
figure('color','w',...
'units','normalized',...
'pos',[0.289165,0.154948,0.409956,0.68099]);
axes('units','normalized','pos',[0.1,0.022,0.89,0.85]);
if strncmpi(GridOpt,'On',2)
mesh(x,y,z,...
'EdgeColor',[0.7,0.7,0.7],...
'FaceAlpha',0,...
'LineWidth',1); % 参考网格线
end
hold on;
axis equal;
axis([-0.1,n+0.1,-0.1,m+0.1,-0.5,0.5]);
view(2);
% 设置X轴和Y轴刻度位置及标签
set(gca,'Xtick',(1:n)-0.5,...
'XtickLabel',XVarNames,...
'Ytick',(1:m)-0.5,...
'YtickLabel',YVarNames,...
'XAxisLocation','top',...
'YDir','reverse',...
'Xcolor',[0.7,0.7,0.7],...
'Ycolor',[0.7,0.7,0.7],...
'TickLength',[0,0]);
axis off
% 绘制填充色块
if strncmpi(FillStyle,'Fill',3)
MyPatch(sx',sy',data',FigShape,FigSize);
end
% 显示数值文本信息
if strncmpi(DisplayOpt,'On',2)
str = num2str(data,'%4.2f');
scale = 0.1*max(n/m,1)/(max(m,n)^0.55);
if strncmpi(TextColor,'Auto',3)
ColorMat = get(gcf,'ColorMap');
nc = size(ColorMat,1);
cid = fix(mapminmax(data',0,1)*nc)+1;
cid(cid<1) = 1;
cid(cid>nc) = nc;
TextColor = ColorMat(cid,:);
for i = 1:numel(data)
text(sx(i),sy(i),0.1,str(i,:),...
'FontUnits','normalized',...
'FontSize',scale,...
'fontweight','bold',...
'HorizontalAlignment','center',...
'Color',TextColor(i,:));
end
else
text(sx,sy,0.1*ones(size(sx)),str,...
'FontUnits','normalized',...
'FontSize',scale,...
'fontweight','bold',...
'HorizontalAlignment','center',...
'Color',TextColor);
end
end
% 设置X轴和Y轴刻度标签的缩进方式
MyTickLabel(gca,FigStyle);
% 添加颜色条
if strncmpi(ColorBar,'On',2)
if any(strncmpi(FigStyle,{'Auto','Triu'},4))
colorbar('Location','EastOutside');
else
colorbar('Location','SouthOutside');
end
end
end
% ---------------------------------------------------
% 调整坐标轴刻度标签子函数
% ---------------------------------------------------
function MyTickLabel(ha,tag)
% 根据显示范围自动调整坐标轴刻度标签的函数
% ha 坐标系句柄值
% tag 调整坐标轴刻度标签的标识字符串,可用取值如下:
% 'Auto' --- 将x轴刻度标签旋转90度,y轴刻度标签不作调整
% 'Tril' --- 将x轴刻度标签旋转90度,并依次缩进,y轴刻度标签不作调整
% 'Triu' --- 将x轴刻度标签旋转90度,y轴刻度标签依次缩进
% Example:
% MyTickLabel(gca,'Tril');
%
% CopyRight:xiezhh(谢中华),2013.1编写
if ~ishandle(ha)
warning('MATLAB:warning2','第一个输入参数应为坐标系句柄');
return;
end
if ~strcmpi(get(ha,'type'),'axes')
warning('MATLAB:warning3','第一个输入参数应为坐标系句柄');
return;
end
axes(ha);
xstr = get(ha,'XTickLabel');
xtick = get(ha,'XTick');
xl = xlim(ha);
ystr = get(ha,'YTickLabel');
ytick = get(ha,'YTick');
yl = ylim(ha);
set(ha,'XTickLabel',[],'YTickLabel',[]);
x = zeros(size(ytick)) + xl(1) - range(xl)/30;
y = zeros(size(xtick)) + yl(1) - range(yl)/70;
nx = numel(xtick);
ny = numel(ytick);
if strncmpi(tag,'Tril',4)
y = y + (1:nx) - 1;
elseif strncmpi(tag,'Triu',4)
x = x + (1:ny) - 1;
end
text(xtick,y,xstr,...
'rotation',90,...
'Interpreter','none',...
'color','r',...
'HorizontalAlignment','left');
text(x,ytick,ystr,...
'Interpreter','none',...
'color','r',...
'HorizontalAlignment','right');
end
% ---------------------------------------------------
% 根据散点数据绘制3维色块图子函数
% ---------------------------------------------------
function MyPatch(x,y,z,FigShape,FigSize)
% 根据散点数据绘制3维色块图
% MyPatch(x,y,z,FigShape,FigSize) x,y,z是实值数组,用来指定色块中心点三维
% 坐标。FigShape是字符串变量,用来指定色块形状。
% FigSize是字符串变量,用来指定色块大小。
%
% CopyRight:xiezhh(谢中华), 2013.01 编写
%
% Example:
% x = rand(10,1);
% y = rand(10,1);
% z = rand(10,1);
% MyPatch(x,y,z,'s','Auto');
%
% 输入参数类型判断
if nargin < 3
error('至少需要三个输入参数');
end
if ~isreal(x) || ~isreal(y) || ~isreal(z)
error('前三个输入应为实值数组');
end
n = numel(z);
if numel(x) ~= n || numel(y) ~= n
error('坐标应等长');
end
if strncmpi(FigSize,'Auto',3) && ~strncmpi(FigShape,'Ellipse',1)
id = (z == 0);
x(id) = [];
y(id) = [];
z(id) = [];
end
if isempty(z)
return;
end
% 求色块顶点坐标
rab1 = ones(size(z));
maxz = max(abs(z));
if maxz == 0
maxz = 1;
end
rab2 = abs(z)/maxz;
if strncmpi(FigShape,'Square',1)
% 方形
if strncmpi(FigSize,'Full',3)
r = rab1;
else
r = sqrt(rab2);
end
SquareVertices(x,y,z,r);
elseif strncmpi(FigShape,'Circle',1)
% 圆形
if strncmpi(FigSize,'Full',3)
r = 0.5*rab1;
else
r = 0.5*sqrt(rab2);
end
CircleVertices(x,y,z,r);
elseif strncmpi(FigShape,'Ellipse',1)
% 椭圆形
a = 0.48 + rab2*(0.57-0.48);
b = (1-rab2).*a;
EllipseVertices(x,y,z,a,b);
elseif strncmpi(FigShape,'Hexagon',1)
% 六边形
if strncmpi(FigSize,'Full',3)
r = 0.5*rab1;
else
r = 0.5*sqrt(rab2);
end
HexagonVertices(x,y,z,r);
else
% 表盘形
if strncmpi(FigSize,'Full',3)
r = 0.45*rab1;
else
r = 0.45*sqrt(rab2);
end
DialVertices(x,y,z,r);
end
end
%--------------------------------------------------
% 求色块顶点坐标并绘制色块的子函数
%--------------------------------------------------
function SquareVertices(x,y,z,r)
% 方形
hx = r/2;
hy = hx;
Xp = [x-hx;x-hx;x+hx;x+hx;x-hx];
Yp = [y-hy;y+hy;y+hy;y-hy;y-hy];
Zp = repmat(z,[5,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function CircleVertices(x,y,z,r)
% 圆形
t = linspace(0,2*pi,30)';
m = numel(t);
Xp = repmat(x,[m,1])+cos(t)*r;
Yp = repmat(y,[m,1])+sin(t)*r;
Zp = repmat(z,[m,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function EllipseVertices(x,y,z,a,b)
% 椭圆形
t = linspace(0,2*pi,30)';
m = numel(t);
t0 = -sign(z)*pi/4;
t0 = repmat(t0,[m,1]);
x0 = cos(t)*a;
y0 = sin(t)*b;
Xp = repmat(x,[m,1]) + x0.*cos(t0) - y0.*sin(t0);
Yp = repmat(y,[m,1]) + x0.*sin(t0) + y0.*cos(t0);
Zp = repmat(z,[m,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function HexagonVertices(x,y,z,r)
% 六边形
t = linspace(0,2*pi,7)';
m = numel(t);
Xp = repmat(x,[m,1])+cos(t)*r;
Yp = repmat(y,[m,1])+sin(t)*r;
Zp = repmat(z,[m,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor','flat');
end
function DialVertices(x,y,z,r)
% 表盘形
% 绘制表盘扇形
maxz = max(abs(z));
t0 = z*2*pi/maxz-pi/2;
t0 = cell2mat(arrayfun(@(x)linspace(-pi/2,x,30)',t0,'UniformOutput',0));
m = size(t0,1);
r0 = repmat(r,[m,1]);
Xp = [x;repmat(x,[m,1]) + r0.*cos(t0);x];
Yp = [y;repmat(y,[m,1]) + r0.*sin(t0);y];
Zp = repmat(z,[m+2,1]);
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor',[0,0,0]);
% 绘制表盘圆周
t = linspace(0,2*pi,30)';
m = numel(t);
Xp = repmat(x,[m,1])+cos(t)*r;
Yp = repmat(y,[m,1])+sin(t)*r;
Zp = repmat(z,[m,1]);
Xp = [Xp;flipud(Xp)];
Yp = [Yp;flipud(Yp)];
Zp = [Zp;flipud(Zp)];
patch(Xp,Yp,Zp,'FaceColor','flat','EdgeColor',[0,0,0]);
end
%--------------------------------------------------------------------------
% 解析输入参数子函数1
%--------------------------------------------------------------------------
function [FigShape,FigSize,FigStyle,FillStyle,DisplayOpt,TextColor,...
XVarNames,YVarNames,ColorBar,GridOpt] = parseInputs(varargin)
if mod(nargin,2)~=0
error('输入参数个数不对,应为成对出现');
end
pnames = {'FigShape','FigSize','FigStyle','FillStyle','DisplayOpt',...
'TextColor','XVarNames','YVarNames','ColorBar','Grid'};
dflts = {'Square','Full','Auto','Fill','On','k','','','Off','On'};
[FigShape,FigSize,FigStyle,FillStyle,DisplayOpt,TextColor,XVarNames,...
YVarNames,ColorBar,GridOpt] = parseArgs(pnames, dflts, varargin{:});
validateattributes(FigShape,{'char'},{'nonempty'},mfilename,'FigShape');
validateattributes(FigSize,{'char'},{'nonempty'},mfilename,'FigSize');
validateattributes(FigStyle,{'char'},{'nonempty'},mfilename,'FigStyle');
validateattributes(FillStyle,{'char'},{'nonempty'},mfilename,'FillStyle');
validateattributes(DisplayOpt,{'char'},{'nonempty'},mfilename,'DisplayOpt');
validateattributes(TextColor,{'char','numeric'},{'nonempty'},mfilename,'TextColor');
validateattributes(XVarNames,{'char','cell'},{},mfilename,'XVarNames');
validateattributes(YVarNames,{'char','cell'},{},mfilename,'YVarNames');
validateattributes(ColorBar,{'char'},{'nonempty'},mfilename,'ColorBar');
validateattributes(GridOpt,{'char'},{'nonempty'},mfilename,'Grid');
if ~any(strncmpi(FigShape,{'Square','Circle','Ellipse','Hexagon','Dial'},1))
error('形状参数只能为Square, Circle, Ellipse, Hexagon, Dial 之一');
end
if ~any(strncmpi(FigSize,{'Full','Auto'},3))
error('图形大小参数只能为Full, Auto 之一');
end
if ~any(strncmpi(FigStyle,{'Auto','Tril','Triu'},4))
error('图形样式参数只能为Auto, Tril, Triu 之一');
end
if ~any(strncmpi(FillStyle,{'Fill','NoFill'},3))
error('图形填充样式参数只能为Fill, NoFill 之一');
end
if ~any(strncmpi(DisplayOpt,{'On','Off'},2))
error('显示数值参数只能为On,Off 之一');
end
if ~any(strncmpi(ColorBar,{'On','Off'},2))
error('显示颜色条参数只能为On,Off 之一');
end
if ~any(strncmpi(GridOpt,{'On','Off'},2))
error('显示网格参数只能为On,Off 之一');
end
end
%--------------------------------------------------------------------------
% 解析输入参数子函数2
%--------------------------------------------------------------------------
function [varargout] = parseArgs(pnames,dflts,varargin)
% Copyright 2010-2011 The MathWorks, Inc.
% $Revision: 1.1.6.2 $ $Date: 2011/05/09 01:27:26 $
% Initialize some variables
nparams = length(pnames);
varargout = dflts;
setflag = false(1,nparams);
unrecog = {};
nargs = length(varargin);
dosetflag = nargout>nparams;
dounrecog = nargout>(nparams+1);
% Must have name/value pairs
if mod(nargs,2)~=0
m = message('stats:internal:parseArgs:WrongNumberArgs');
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
% Process name/value pairs
for j=1:2:nargs
pname = varargin{j};
if ~ischar(pname)
m = message('stats:internal:parseArgs:IllegalParamName');
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
mask = strncmpi(pname,pnames,length(pname)); % look for partial match
if ~any(mask)
if dounrecog
% if they've asked to get back unrecognized names/values, add this
% one to the list
unrecog((end+1):(end+2)) = {varargin{j} varargin{j+1}};
continue
else
% otherwise, it's an error
m = message('stats:internal:parseArgs:BadParamName',pname);
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
elseif sum(mask)>1
mask = strcmpi(pname,pnames); % use exact match to resolve ambiguity
if sum(mask)~=1
m = message('stats:internal:parseArgs:AmbiguousParamName',pname);
throwAsCaller(MException(m.Identifier, '%s', getString(m)));
end
end
varargout{mask} = varargin{j+1};
setflag(mask) = true;
end
% Return extra stuff if requested
if dosetflag
varargout{nparams+1} = setflag;
if dounrecog
varargout{nparams+2} = unrecog;
end
end
end```
```css
function TextHandle = rotateticklabel(ha,tag,rot)
% 旋转坐标轴刻度标签的函数
% ha 坐标系句柄(默认为当前坐标系)
% tag 坐标轴标识字符串('X'或'Y'),默认旋转X轴标签
% rot 旋转角度(单位:度)
%
% Example:
% x = 0:0.05:2*pi;
% y = sin(x);
% plot(x,y);
% str = '这里是0|这里是1|这里是2|这里是3|这里是4|这里是5|这里是6|这里是7';
% set(gca,'xtick',0:7,'xticklabel',str);
%
% rotateticklabel(gca,'x',-30);
%
% CopyRight:xiezhh(谢中华)
if ~ishandle(ha)
warning('第一个输入参数应为坐标系句柄');
return;
end
if ~strcmpi(get(ha,'type'),'axes')
warning('第一个输入参数应为坐标系句柄');
return;
end
if nargin == 1
tag = 'X';
rot = 0;
elseif nargin == 2
if isnumeric(tag) && isscalar(tag)
rot = tag;
tag = 'X';
elseif ischar(tag) && (strncmpi(tag,'x',1) || strncmpi(tag,'y',1))
rot = 0;
else
warning('输入参数类型错误');
return;
end
else
if ~isnumeric(rot) || ~isscalar(rot)
warning('输入参数类型错误');
end
if ~ischar(tag) || (~strncmpi(tag,'x',1) && ~strncmpi(tag,'y',1))
warning('输入参数类型错误');
end
end
oldxticklabel = findobj('type','text','tag','oldxticklabel');
oldyticklabel = findobj('type','text','tag','oldyticklabel');
if strncmpi(tag,'x',1)
if isempty(oldxticklabel)
str = get(ha,'XTickLabel');
x = get(ha,'XTick');
yl = ylim(ha);
set(ha,'XTickLabel',[]);
y = zeros(size(x)) + yl(1) - range(yl)/70;
TextHandle = text(x,y,str,'rotation',rot,...
'Interpreter','none','tag','oldxticklabel');
else
set(oldxticklabel,'rotation',rot);
TextHandle = oldxticklabel;
end
else
if isempty(oldyticklabel)
str = get(ha,'YTickLabel');
y = get(ha,'YTick');
xl = xlim(ha);
set(ha,'YTickLabel',[]);
x = zeros(size(y)) + xl(1) - range(xl)/10;
TextHandle = text(x,y,str,'rotation',rot,...
'Interpreter','none','tag','oldyticklabel');
else
set(oldyticklabel,'rotation',rot);
TextHandle = oldyticklabel;
end
end
rot = mod(rot,360);
if rot>=0 && rot<180
set(TextHandle,'HorizontalAlignment','right');
else
set(TextHandle,'HorizontalAlignment','left');
end```
>> Chapter19
类 LinearModel 的方法:
addTerms compact gather plotAdjustedResponse plotPartialDependence random
anova disp partialDependence plotDiagnostics plotResiduals removeTerms
coefCI dwtest plot plotEffects plotSlice step
coefTest feval plotAdded plotInteraction predict
类 LinearModel 的属性:
Residuals
Fitted
Diagnostics
MSE
Robust
RMSE
Formula
LogLikelihood
DFE
SSE
SST
SSR
CoefficientCovariance
CoefficientNames
NumCoefficients
NumEstimatedCoefficients
Coefficients
Rsquared
ModelCriterion
VariableInfo
NumVariables
VariableNames
NumPredictors
PredictorNames
ResponseName
NumObservations
Steps
ObservationInfo
Variables
ObservationNames
nlm =
非线性回归模型:
y ~ 0
系数:
类 NonLinearModel 的方法:
coefCI disp partialDependence plotPartialDependence plotSlice random
coefTest feval plotDiagnostics plotResiduals predict
类 NonLinearModel 的属性:
MSE
Iterative
Robust
Residuals
Fitted
RMSE
Diagnostics
WeightedResiduals
VariableInfo
NumVariables
VariableNames
NumPredictors
PredictorNames
ResponseName
NumObservations
ObservationInfo
Variables
ObservationNames
Formula
LogLikelihood
DFE
SSE
SST
SSR
CoefficientCovariance
CoefficientNames
NumCoefficients
NumEstimatedCoefficients
Coefficients
Rsquared
ModelCriterion
R =
1.0000 -0.7095
-0.7095 1.0000
mdl1 =
线性回归模型:
y ~ 1 + x1
估计系数:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) 3115.4 223.06 13.967 2.0861e-14
x1 -76.962 14.197 -5.4211 7.8739e-06
观测值数目: 31,误差自由度: 29
均方根误差: 383
R 方: 0.503,调整 R 方 0.486
F 统计量(常量模型): 29.4,p 值 = 7.87e-06
ynew =
1.0e+03 *
2.7306
1.1913
mdl2 =
线性回归模型:
y ~ 1 + x1
估计系数:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) 2983.8 121.29 24.601 4.8701e-19
x1 -63.628 7.7043 -8.2587 1.3088e-08
观测值数目: 27,误差自由度: 25
均方根误差: 201
R 方: 0.732,调整 R 方 0.721
F 统计量(常量模型): 68.2,p 值 = 1.31e-08
mdl3 =
线性回归模型(稳健拟合):
y ~ 1 + x1
估计系数:
Estimate SE tStat pValue
________ ______ ______ __________
(Intercept) 3034.8 182.01 16.674 2.1276e-16
x1 -68.3 11.584 -5.896 2.1194e-06
观测值数目: 31,误差自由度: 29
均方根误差: 313
R 方: 0.551,调整 R 方 0.535
F 统计量(常量模型): 35.5,p 值 = 1.78e-06
nlm1 =
非线性回归模型(稳健拟合):
y ~ beta1*exp(beta2/(x + beta3))
估计系数:
Estimate SE tStat pValue
________ ________ _______ __________
beta1 52.377 0.1449 361.46 0
beta2 -0.25951 0.016175 -16.044 6.4817e-53
beta3 0.76038 0.072948 10.423 1.7956e-24
观测值数目: 1281,误差自由度: 1278
均方根误差: 1.66
R 方: 0.747,调整 R 方 0.747
F 统计量(零模型): 4.64e+05,p 值 = 0
ci1 =
52.0923 52.6609
-0.2912 -0.2278
0.6173 0.9035
nlm2 =
非线性回归模型(稳健拟合):
y ~ beta1*exp(beta2/(x + beta3))
估计系数:
Estimate SE tStat pValue
________ ________ _______ __________
beta1 52.369 0.12693 412.6 0
beta2 -0.26243 0.014592 -17.984 5.9309e-64
beta3 0.78167 0.067002 11.666 8.2311e-30
观测值数目: 1159,误差自由度: 1156
均方根误差: 1.37
R 方: 0.807,调整 R 方 0.807
F 统计量(零模型): 6.11e+05,p 值 = 0
R =
1.0000 -0.3201 -0.0777 -0.8645 -0.5130 -0.4573
-0.3201 1.0000 -0.1809 0.1845 -0.1092 -0.3757
-0.0777 -0.1809 1.0000 0.1121 0.0520 0.1410
-0.8645 0.1845 0.1121 1.0000 0.6132 0.4383
-0.5130 -0.1092 0.0520 0.6132 1.0000 0.3303
-0.4573 -0.3757 0.1410 0.4383 0.3303 1.0000
P =
1.0000 0.1273 0.7181 0.0000 0.0104 0.0247
0.1273 1.0000 0.3976 0.3882 0.6116 0.0704
0.7181 0.3976 1.0000 0.6022 0.8095 0.5111
0.0000 0.3882 0.6022 1.0000 0.0014 0.0322
0.0104 0.6116 0.8095 0.0014 1.0000 0.1149
0.0247 0.0704 0.5111 0.0322 0.1149 1.0000
mmdl1 =
线性回归模型:
y ~ 1 + x1 + x2 + x3 + x4 + x5
估计系数:
Estimate SE tStat pValue
_________ ________ ________ __________
(Intercept) 121.17 17.406 6.961 1.6743e-06
x1 -0.34712 0.14353 -2.4185 0.026406
x2 -0.016719 0.087353 -0.19139 0.85036
x3 -4.2903 1.0268 -4.1784 0.00056473
x4 -0.039917 0.094237 -0.42357 0.67689
x5 -0.15866 0.078847 -2.0122 0.059407
观测值数目: 24,误差自由度: 18
均方根误差: 2.8
R 方: 0.816,调整 R 方 0.765
F 统计量(常量模型): 16,p 值 = 4.46e-06
VIF =
1.5974
1.0657
2.4044
1.7686
1.6985
mmdl2 =
线性回归模型:
y ~ 1 + x1 + x3 + x5
估计系数:
Estimate SE tStat pValue
________ _______ _______ __________
(Intercept) 119.5 11.81 10.118 7.4559e-09
x1 -0.36229 0.11272 -3.2141 0.0048108
x3 -4.0411 0.62858 -6.4289 4.7386e-06
x5 -0.17739 0.05977 -2.9678 0.0082426
观测值数目: 22,误差自由度: 18
均方根误差: 2.11
R 方: 0.862,调整 R 方 0.84
F 统计量(常量模型): 37.6,p 值 = 5.81e-08
mmdl3 =
线性回归模型:
y ~ 1 + x1^2 + x1*x2 + x2^2 + x1*x3 + x2*x3 + x3^2 + x1*x4 + x2*x4 + x3*x4 + x4^2 + x1*x5 + x2*x5 + x3*x5 + x4*x5 + x5^2
估计系数:
Estimate SE tStat pValue
__________ _________ ________ _________
(Intercept) 1804.1 176.67 10.211 0.0020018
x1 -26.768 3.3174 -8.069 0.0039765
x2 -16.422 1.4725 -11.153 0.0015449
x3 -7.2417 17.328 -0.41792 0.70412
x4 1.7071 1.5284 1.1169 0.34543
x5 -5.5878 1.2082 -4.6248 0.019034
x1^2 0.034031 0.02233 1.524 0.22489
x1:x2 0.18853 0.014842 12.702 0.0010526
x2^2 -0.0024412 0.0030872 -0.79075 0.48684
x1:x3 0.23808 0.21631 1.1006 0.35145
x2:x3 -0.56157 0.087918 -6.3874 0.0077704
x3^2 0.68822 0.63574 1.0826 0.35825
x1:x4 0.016786 0.015763 1.0649 0.36502
x2:x4 0.0030961 0.0058481 0.52942 0.63319
x3:x4 -0.065623 0.071279 -0.92065 0.42513
x4^2 -0.016381 0.0047701 -3.4342 0.041411
x1:x5 0.03502 0.011535 3.0359 0.056047
x2:x5 0.067888 0.0063552 10.682 0.0017537
x3:x5 0.17506 0.063871 2.7408 0.071288
x4:x5 -0.0016748 0.0056432 -0.29679 0.78599
x5^2 -0.007748 0.0027112 -2.8577 0.064697
观测值数目: 24,误差自由度: 3
均方根误差: 0.557
R 方: 0.999,调整 R 方 0.991
F 统计量(常量模型): 123,p 值 = 0.00104
1。正在删除 x4:x5, FStat = 0.088084, pValue = 0.78599
2。正在删除 x2:x4, FStat = 0.49518, pValue = 0.52043
3。正在删除 x2^2, FStat = 0.55596, pValue = 0.48944
4。正在删除 x1:x3, FStat = 2.0233, pValue = 0.20475
5。正在删除 x3^2, FStat = 1.7938, pValue = 0.22232
6。正在删除 x3:x4, FStat = 1.7098, pValue = 0.22734
mmdl4 =
线性回归模型:
y ~ 1 + x1^2 + x1*x2 + x2*x3 + x1*x4 + x4^2 + x1*x5 + x2*x5 + x3*x5 + x5^2
估计系数:
Estimate SE tStat pValue
__________ _________ _______ __________
(Intercept) 1916.6 106.48 17.999 2.2957e-08
x1 -29.485 1.6156 -18.251 2.0321e-08
x2 -15.841 0.92505 -17.124 3.553e-08
x3 3.3267 4.4986 0.7395 0.47845
x4 0.757 0.43986 1.721 0.11936
x5 -6.547 0.69061 -9.4801 5.5705e-06
x1^2 0.060353 0.0051667 11.681 9.6821e-07
x1:x2 0.17622 0.010126 17.403 3.0846e-08
x2:x3 -0.46789 0.050314 -9.2994 6.5277e-06
x1:x4 0.034115 0.0041517 8.2173 1.7857e-05
x4^2 -0.019258 0.0032306 -5.9612 0.00021239
x1:x5 0.045394 0.0050247 9.0342 8.2768e-06
x2:x5 0.063051 0.0043992 14.332 1.6742e-07
x3:x5 0.165 0.025546 6.4588 0.00011693
x5^2 -0.0052175 0.0016766 -3.1119 0.01248
观测值数目: 24,误差自由度: 9
均方根误差: 0.521
R 方: 0.997,调整 R 方 0.992
F 统计量(常量模型): 201,p 值 = 1.82e-09
mmdl5 =
线性回归模型:
y ~ 1 + x1^2 + x1*x2 + x2:x3 + x1:x4 + x4^2 + x1*x5 + x2*x5 + x3:x5 + x5^2
估计系数:
Estimate SE tStat pValue
__________ _________ _______ __________
(Intercept) 1809.1 94.501 19.143 8.544e-10
x1 -27.514 1.3891 -19.808 5.9281e-10
x2 -14.931 0.84624 -17.644 2.0412e-09
x5 -5.9038 0.58088 -10.164 6.2848e-07
x1^2 0.056747 0.0052153 10.881 3.1609e-07
x1:x2 0.1671 0.0097032 17.221 2.6436e-09
x2:x3 -0.46162 0.048949 -9.4306 1.3239e-06
x1:x4 0.037604 0.0037157 10.12 6.5604e-07
x4^2 -0.013934 0.0014402 -9.6755 1.0269e-06
x1:x5 0.039071 0.0042784 9.1321 1.8171e-06
x2:x5 0.059989 0.0041019 14.625 1.4875e-08
x3:x5 0.18165 0.022175 8.1915 5.2127e-06
x5^2 -0.0057969 0.0016226 -3.5726 0.0043753
观测值数目: 24,误差自由度: 11
均方根误差: 0.568
R 方: 0.995,调整 R 方 0.99
F 统计量(常量模型): 197,p 值 = 4.9e-11
mnlm =
非线性回归模型:
y ~ sqrt((x1 - b1)^2 + (x2 - b2)^2 + b3^2)/(60*b4) + b5
估计系数:
Estimate SE tStat pValue
________ _________ _______ __________
b1 2200.5 0.53366 4123.5 1.5922e-17
b2 1399.9 0.48183 2905.4 9.168e-17
b3 35.144 61.893 0.56782 0.5947
b4 2.9994 0.0041439 723.82 9.5533e-14
b5 6.9863 0.02087 334.75 4.515e-12
观测值数目: 10,误差自由度: 5
均方根误差: 0.00591
R 方: 1,调整 R 方 1
F 统计量(常量模型): 8.3e+05,p 值 = 9.75e-15
>> ```














