一元非线性回归方程(matplotlib)
一元非线性回归模型通用表达式:
y = a n x n + a n − 1 x n − 1 + . . . . . . + a 0 x 0 y = a_nx^n + a_{n-1}x^{n-1}+......+a_0x^0 y=anxn+an−1xn−1+......+a0x0
但是一般不直接求解一元非线性方程,而是将其转化为多重线性方程来求解,好处在于可以把复杂的一元非线性方程变为简单的多线性方程。
例如:
假设要拟合的方程为:
y = a 2 x 2 + a 1 x 1 + a 0 x 0 y = a_2x^2 + a_1x^1 + a_0x^0 y=a2x2+a1x1+a0x0
转化为:
y = a 2 x 2 ˉ + a 1 x 1 ˉ + a 0 x 0 ˉ y = a_2\bar{x_2} + a_1\bar{x_1} + a_0\bar{x_0} y=a2x2ˉ+a1x1ˉ+a0x0ˉ
##下面通过一个案例来说明:
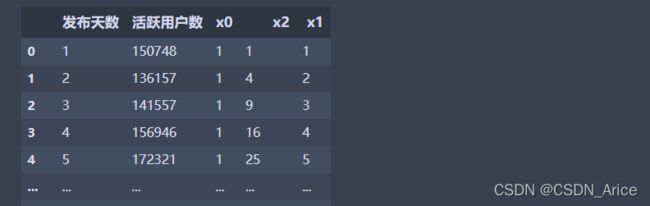
问题:上线某产品,记录每天的活跃用户数,部分数据如下,现在希望通过发布天数来预测活跃用户数能达到多少?

根据预测目标确定自变量因变量:
import pandas as pd
data = pd.read_csv(
'D:\example_csv\一元非线性回归.csv',
encoding = 'ANSI')
x = data[['发布天数']] #作为自变量
y = data[['活跃用户数']]#作为因变量
绘制散点图,确认回归模型类型:
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']#使标题乱码变为中文
plt.figure(figsize = (8,4))
plt.title('发布天数与活跃用户数',#标题字体比坐标轴更大些
fontsize = 20)
plt.xlabel('发布天数',fontsize = 15)
plt.ylabel('活跃用户数',fontsize = 15)
plt.plot(x,y,color = 'blue')
不同的表达式,对模型的拟合效果不一样,因此我们需要尽可能多的对多个多项式进行尝试,看看哪个多项式效更好。
#尝试二重线性回归
data['x0'] = data.发布天数.pow(0)
data['x1'] = data.发布天数.pow(1)
data['x2'] = data.发布天数.pow(2)
from sklearn.linear_model import LinearRegression
x1 = data[['x0','x1','x2']]
y1 = data[['活跃用户数']]
lrModel = LinearRegression()
lrModel.fit(x1,y1)#进行模型训练
lrModel.coef_
lrModel.intercept_#截距
lrModel.score(x1,y1)
得到的数据不错,一般来说,当使用多重线性回归去近似拟合非线性回归时,多项式的阶数越高,效果越好,但达到做好的效果后,拟合的效果又会回落。

通过sklearn.preprocessing.PolynomialFeatures来找到最好的阶数:
使用方法如下:
from sklearn.preprocessing import PolynomialFeatures
x = data[['发布天数']]
ds = []
scores = []
for d in range(2,20): #从第2阶开始尝试到第20阶
ds.append(d)
p1 = PolynomialFeatures(degree = d)
x_d = p1.fit_transform(x) #转化
lrModel = LinearRegression()
lrModel.fit(x_d,y)
scores.append(lrModel.score(x_d,y))
dScores = pd.DataFrame({
'阶次':ds,
'模型得分':scores
})
执行代码,部分结果如下:

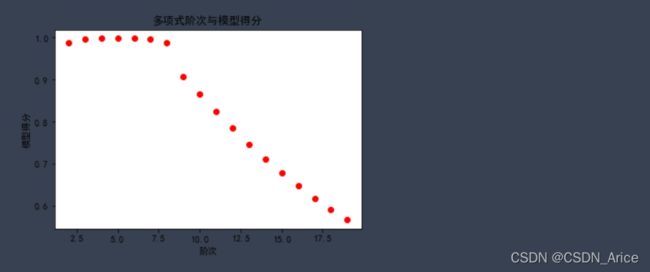
可以发现在阶次3之后,模型的得分虽然有小幅度的提升,但是提升的空间非常有限,在模型得分接近的情况下,我们尽量选择简单的模型。
通过散点图可以更清晰的看出模型得分变化趋势:
plt.xlabel('阶次')
plt.ylabel('模型得分')
plt.title('多项式阶次与模型得分')
plt.scatter(ds,scores,color = 'red')
对回归模型进行检验:
p2 = PolynomialFeatures(degree = 3)
x_3 = p2.fit_transform(x)
lrModel = LinearRegression()
lrModel.fit(x_3,y)
lrModel.score(x_3,y)
模型精度为:0.997,拟合效果很不错。

最后进行活跃用户数预测:
px3 = pd.DataFrame({
"发布天数":[150] #天数可以自己选择
})
px_3 = p2.fit_transform(px3)
lrModel.predict(px_3)