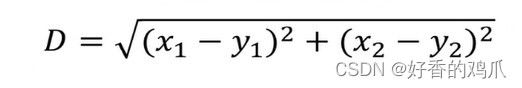层次聚类,概念+示例,超详细!!!
介绍
层次聚类(Hierarchical Clustering)是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中,不同类别的原始数据点是树的最低层,树的顶层是一个聚类的根节点。
创建聚类树有自下而上合并 和 自上而下分裂的两种方法。
举例
作为一家公司的人力资源部经理,你可以把所有的雇员组织成较大的簇,如主管、经理和职员;然后你可以进一步划分为较小的簇,例如,职员簇可以进一步划分为子簇:高级职员,一般职员和实习人员。所有的这些簇形成了层次结构,可以很容易地对各层次上的数据进行汇总或特征化。
优点
层次聚类算法相比划分聚类算法的优点之一就是可以在不同的层次上展示数据集的聚类情况。
基于层次的聚类算法是可以凝聚或者分裂的,取决于自下而上还是自上而下
自下而上的合并算法
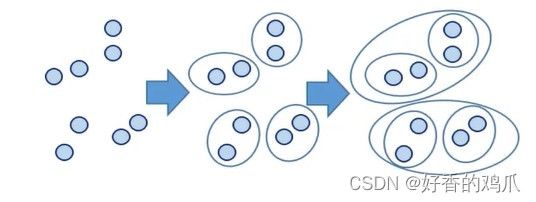
层次聚类的合并算法通过计算两类数据点间的相似性,对所有数据点中最为相似的两个数据点进行组合,并反复迭代这一过程。
简单来说,层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性,距离越小,相似度越高。并将距离最近的两个数据点或者类别进行组合,生成聚类树。
相似度计算
层次聚类使用欧式距离来计算不同类别数据点间的距离(相似度)。
两个组合数据点间的距离
计算两个组合数据点间的距离的方法有三种,Single Linkage,Complete Linkage和Average Linkage
举例
from scipy.cluster.hierarchy import linkage,dendrogram
import matplotlib.pylab as plt
import numpy as np
data = [[1,3],[2,1],[1,2],[4,4],[4,6],[6,7]]
data = np.array(data) #把列表转化为数组 因为列表不存在维度,而数组是有维度的
z = linkage(data,method='single')
dendrogram(z) #形成树状图
plt.show()
linkage函数
功能:进行层次聚类/凝聚聚类
参数1:MxN的二维矩阵,N个样本,M个维度。
参数2:’single’:一范数距离
d(u,v) = min(dist(u[i],u[j]))
对于u中所有点i和v中所有点j。这被称为最近邻点算法
’complete’:无穷范数距离
d(u,v) = max(dist(u[i],u[j]))
对于u中所有点i和v中所有点j。这被称为最远邻点算法。
’average’:平均距离
平均距离,类与类间所有pairs距离的平均
’centroid’:二范数距离
’ward’:离差平方和距离
返回值:返回值:(N-1)*4 的矩阵 Z
拓展:
fcluster(Z, t, criterion=’ ')
fcluster 用于处理linkage的返回值Z
-
参数Z:linkage函数的返回值Z
-
参数scalar:形参扁平簇的阈值
-
参数criterion:
inconsistent’:预设的,如果一个集群节点及其所有后代的不一致值小于或等于 t,那么它的所有叶子后代都属于同一个平面集群。当没有非单例集群满足此条件时,每个节点都被分配到自己的集群中。
’distance’:每个簇的距离不超过 t。
返回每一个特征的类别