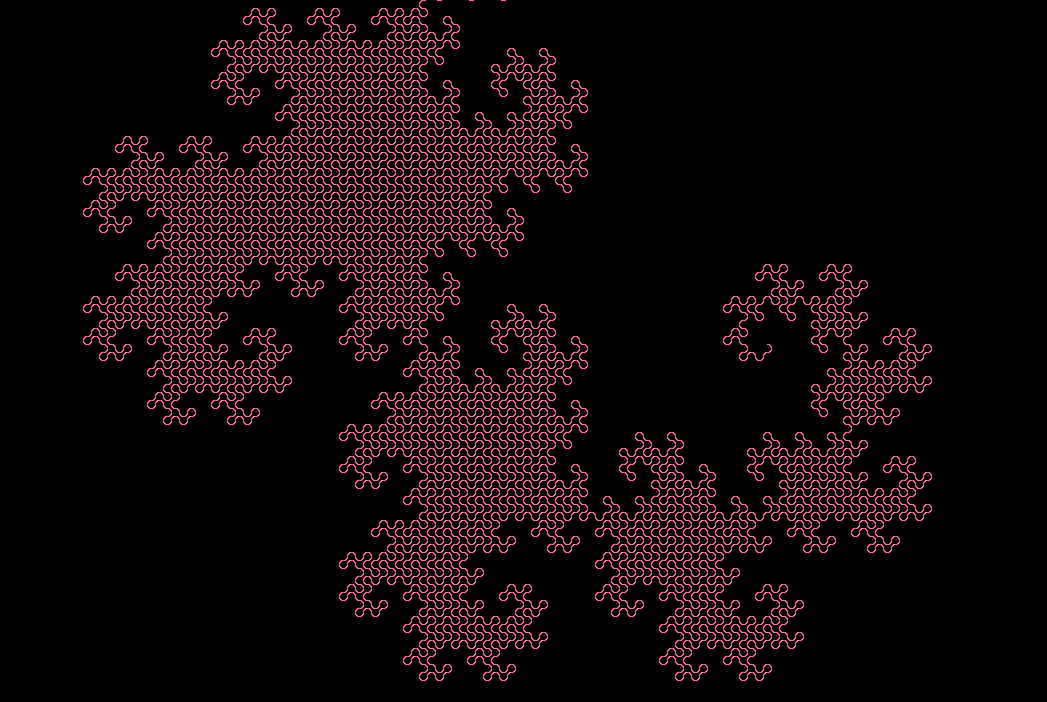用 Python 绘制龙形曲线
本文将学习什么是龙形曲线,如何生成龙形曲线,以及如何在Python中创建龙形曲线。
什么是龙形曲线?
龙形曲线是一个分形,在数学中,分形是一个术语,用来描述在任意小的尺度上包含详细结构的几何形状。许多分形在不同的尺度上看起来很相似,如曼德勃罗集的连续放大,如图所示。
龙形曲线可能最常被认为是由反复对折
的纸条产生的形状,尽管还有其他被称为龙形曲线的曲线是以不同方式产生的。
如何构建龙形曲线?
龙形曲线可以通过折叠纸条来构建,这也是最初发现龙形曲线的方法。拿一张纸条,将其向右对折。再把它向右折成两半。如果现在把纸条打开,把每个折痕都解开,变成一个90度的转弯,转弯的顺序就是RRL,也就是龙形曲线的第二次迭代。再把条状物向右对折,展开后的条状物的转弯顺序现在是RRLRRLL —— 龙形曲线的第三次迭代。继续将条状物向右对折,创造出更多迭代的曲线。
算法
这一连串纸条的折叠模式,作为右(R)和左(L)折叠的序列,是。
-
第一次迭代:R
-
第二次迭代:R R L
-
第三次迭代:R R L R L L
-
第四次迭代:R R L R L R R L L R R L L
每个迭代都可以通过复制前一个迭代,得到一个R,然后按相反的顺序复制前一个迭代的第二个副本,L和R字母互换。
用 Python 进行实现
让我们一步步地分解这个算法。下面就是该算法:每个迭代都可以通过复制前一个迭代,然后得到一个R,然后是前一个迭代的第二个副本,顺序相反,L和R的字母互换。
步骤:
1、每个迭代都可以通过复制前一个迭代来找到。
sequence = sequence
2、得到R
sequence = sequence+R
3、然后以相反的顺序复制前一次迭代的第二个副本,L和R字母互换。
sequence = sequence+R+swapLetters(sequence[::-1])
如果我们把这一切放在一个Python函数中,我们会得到以下结果:
R = "R"
L = "L"
def iterate(sequence: str) -> str:
sequence = sequence+R+swapLetters(sequence[::-1])
return sequence
def swapLetters(sequence: str) -> str:
newSequence = ""
for letter in sequence:
if letter == R:
newSequence = newSequence + L
else:
newSequence = newSequence + R
return newSequence
我们可以创建另一个函数来生成一个特定的迭代,像这样:
def dragon(n_iterations: int) -> str:
"""Takes in a number n, an return the dragon curve sequence i.e.:
When n=2, returns "RRL"
Args:
n_iterations (int): number of iterations of the dragon curve
Returns:
str: The dragon curve Sequence
"""
initial_sequence = R
for i in range(0, n_iterations):
initial_sequence = iterate(initial_sequence)
return initial_sequence
我们可以把所有东西放在一个名为dragon.py的python文件中。
让我们来实现图形
为了实现图形,我们将使用一个叫做turtle的python模块,它提供了海龟图形基础。
1、导入库
from dragon import dragon, R
from turtle import Turtle, Screen
2、Turtle 设置。在这里,我们定义了Turtle 的绘制速度,龙形曲线的颜色,然后我们隐藏Turtle。
# Turtle Setup
turtle = Turtle("turtle")
turtle.hideturtle()
turtle.speed("fastest")
turtle.color("#ff69aa")
3、屏幕设置。我们添加一个标题,一个背景颜色,然后是屏幕大小(调整turtle画布的大小),以及设置,即设置主窗口的大小和位置。
# Screen Setup
screen = Screen()
screen.title("Dragon Curve")
screen.bgcolor("black")
screen.screensize(1920*3, 1080*3)
screen.setup(width=1.0, height=1.0, startx=None, starty=None)
4、绘制龙形曲线。在这里,我们遍历从dragon(17)得到的序列,即第17个序列,根据字母是R还是L,我们向右或向左走。
# Draw
LENGTH = 10
turtle.forward(LENGTH)
for element in dragon(17):
if element == R:
turtle.right(90)
turtle.forward(LENGTH)
else:
turtle.left(90)
turtle.forward(LENGTH)
5、完成后要退出程序。
turtle.color("white")
turtle.write("click to exit", font=("Calibri", 16, "bold"))
screen.exitonclick()
最终结果
如果我们把所有的东西放在两个文件里,我们会得到。
dragon.py
R = "R"
L = "L"
def iterate(sequence: str) -> str:
sequence = sequence+R+swapLetters(sequence[::-1])
return sequence
def swapLetters(sequence: str) -> str:
newSequence = ""
for letter in sequence:
if letter == R:
newSequence = newSequence + L
else:
newSequence = newSequence + R
return newSequence
def dragon(n_iterations: int) -> str:
initial_sequence = R
for i in range(0, n_iterations):
initial_sequence = iterate(initial_sequence)
return initial_sequence
app.py
from dragon import dragon, R
from turtle import Turtle, Screen
# Turtle setup
turtle = Turtle("turtle")
turtle.hideturtle()
turtle.speed("fastest")
turtle.color("#ff69aa")
# Screen setup
screen = Screen()
screen.title("Dragon Curve")
screen.bgcolor("black")
screen.screensize(1920*3, 1080*3)
screen.setup(width=1.0, height=1.0, startx=None, starty=None)
# Draw
LENGTH = 10
turtle.forward(LENGTH)
for element in dragon(17):
if element == R:
turtle.right(90)
turtle.forward(LENGTH)
else:
turtle.left(90)
turtle.forward(LENGTH)
# When finished, click to exit
turtle.color("white")
turtle.write("click to exit", font=("Calibri", 16, "bold"))
screen.exitonclick()
而这将会是这样:
让它更圆
如果你喜欢,可以改变风格,不使用直线,而是使用圆形,只需改变以下代码。
# Draw
LENGTH = 10
for element in dragon(17):
if element == R:
turtle.circle(-4, 90, 36)
else:
turtle.circle(4, 90, 36)
而最终的结果将如下图所示:
GitHub地址:
https://github.com/francofgp/dragon-curve
总结
乍一看似乎很难的东西原来很简单,通过一步步的分解,我们已经学会了如何在Python中轻松地创建这个惊人的分形。